Fractions Fun: Free Comparing Worksheet With Answers

If you've ever pondered how children might grasp the tricky concept of fractions, then this post is tailor-made for you. Fractions can be a challenging part of mathematics for many, but with the right tools, like worksheets, it becomes an engaging journey into understanding numbers and quantities.
Fractions Explained Simply
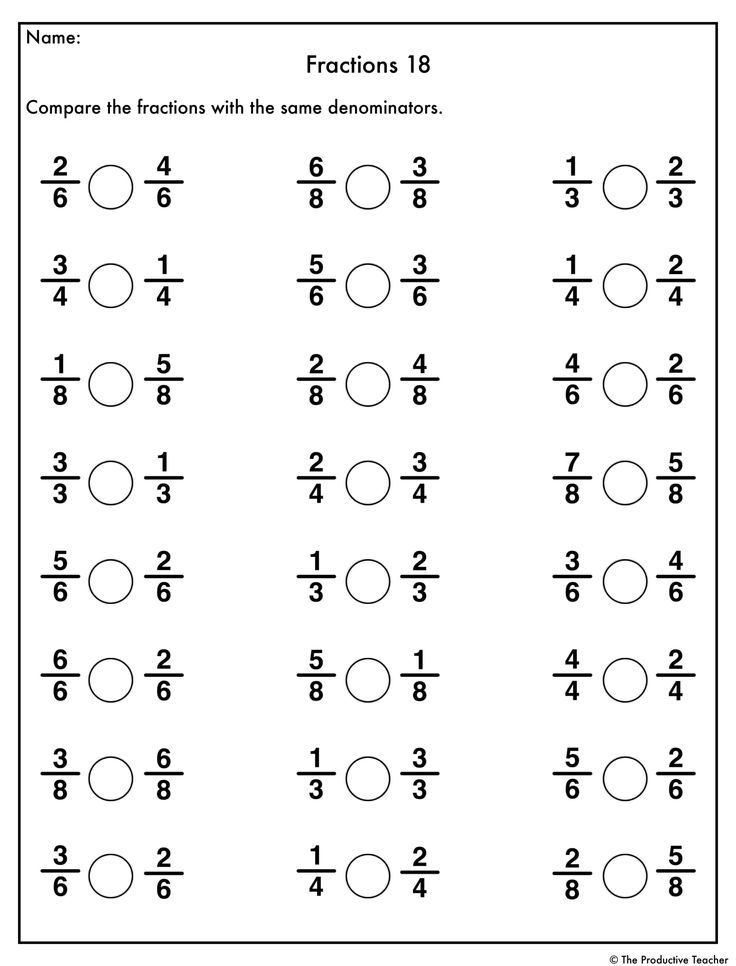
Fractions represent parts of a whole or a group. They have a numerator (the top number) which shows the number of parts we're talking about, and a denominator (the bottom number) which tells us how many equal parts the whole has been divided into. To illustrate, if you have a pizza cut into 8 slices and you eat 3, you would represent this as 3/8 of the pizza.
Comparing Fractions

Here's where things get a bit trickier for young learners:
- Unlike numerators or denominators: When fractions have different denominators, comparing them isn't as straightforward as it is with whole numbers. The process involves finding a common denominator or using other comparison methods.
- Equivalent fractions: These are fractions that represent the same amount, although they might look different on paper. For instance, 1/2 is the same as 2/4.

Free Worksheet on Comparing Fractions

To help demystify fractions, here's a free worksheet tailored for learning comparison:
| Fraction A | Fraction B | Which is Bigger? |
|---|---|---|
| 3/4 | 2/3 | 3/4 |
| 1/2 | 5/8 | 5/8 |
| 7/10 | 7/12 | 7/10 |
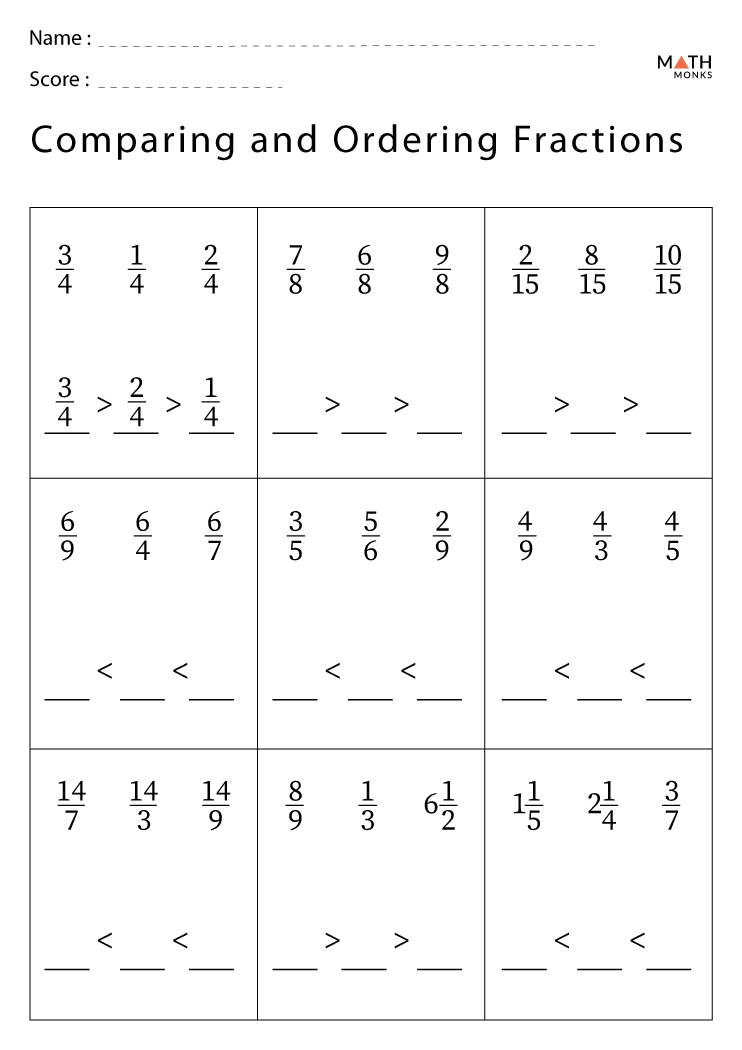
📝 Note: For students, practicing with such worksheets not only sharpens their comparison skills but also deepens their understanding of fractional relationships.
Why Use Worksheets?

Worksheets are invaluable for several reasons:
- Reinforce Learning: Repetition in a fun, varied format helps to solidify concepts.
- Visual Aids: Fractions are visual; seeing them on paper aids comprehension.
- Engage in Problem Solving: Worksheets challenge students to apply what they've learned in diverse scenarios.
Strategies for Comparing Fractions

Let's dive into some effective strategies:
- Cross-Multiplying: A quick way to compare fractions. Multiply the numerator of one fraction by the denominator of the other, and vice versa. The fraction with the larger product is the larger fraction.
- Converting to a Common Denominator: Find the least common multiple (LCM) of the denominators, then convert both fractions so they have this LCM as their denominator. Comparing numerators then becomes easier.
- Visual Comparison: Draw fractions or use fraction strips for a visual approach to understanding and comparing fractions.
🧮 Note: Teaching multiple methods allows students to choose what resonates with them, facilitating a deeper understanding of fractions.
Tips for Teaching Fractions

To make fraction teaching more effective:
- Use real-life examples: From slicing apples to dividing cookies, real-world examples bring fractions to life.
- Practice estimation: Before calculating, estimate which fraction might be larger to sharpen number sense.
- Make it fun: Games or interactive activities like "Who has the most?" can make learning fractions playful.
Throughout this journey of comparing fractions, the understanding of how fractions relate to each other becomes clear. This knowledge is not just essential for academic success but also for everyday life, from dividing resources fairly to understanding proportions in cooking.
To sum up, mastering fractions, especially comparing them, is a crucial skill for students. With engaging tools like worksheets and a strategic approach, we can make this process enjoyable and fruitful. Let’s continue to explore, practice, and make fractions fun!
Why is it important to teach students how to compare fractions?
+
Comparing fractions helps develop number sense, which is crucial for understanding relationships between numbers, solving real-world problems, and laying the foundation for more complex mathematical concepts in the future.
What can I do if my child struggles with understanding fractions?

+
Use tangible examples like cutting food, dividing toys, or even playing with playdough to show fractions physically. Reinforce with visuals like fraction strips or interactive websites designed for learning fractions.
Are there other methods for comparing fractions besides the ones mentioned?

+
Yes, some students might find success with converting all fractions to decimals or percentages for comparison. Another method is finding equivalent fractions with like denominators, making the comparison straightforward.



