5 Easy Tips to Compare Fractions Free Worksheet
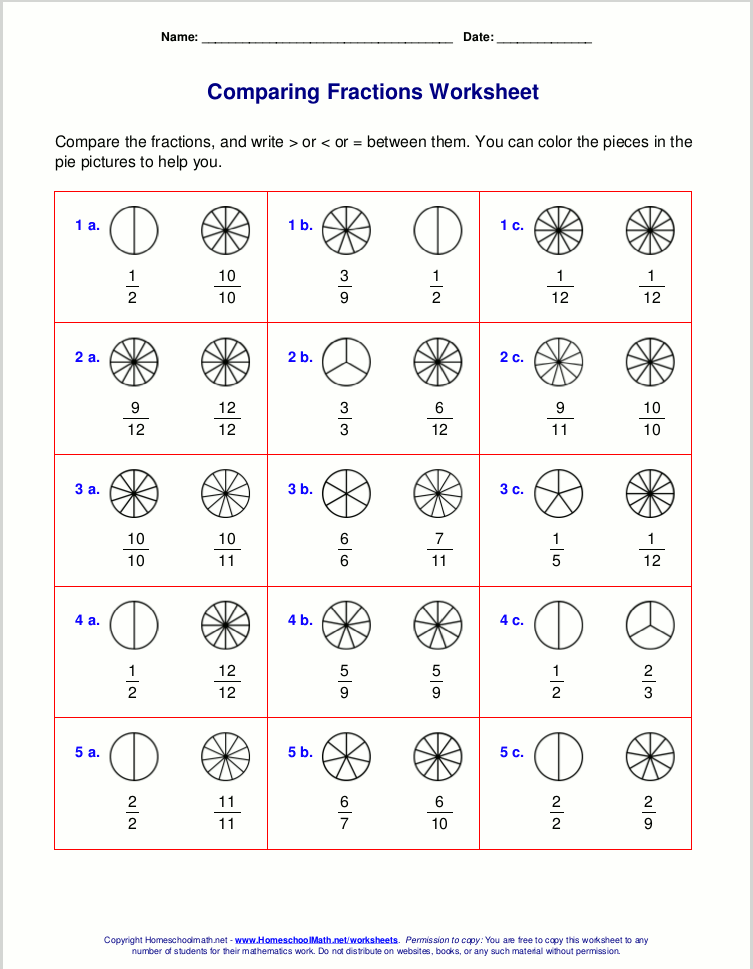
Fractions can often be a tricky concept for both students and adults to master, especially when it comes to comparing different values. Yet, understanding how to compare fractions is crucial for everyday applications, from cooking to budgeting, and for advancing in mathematics. In this comprehensive guide, we'll delve into easy-to-understand methods for comparing fractions. Additionally, we'll provide you with a free worksheet that you can use to practice these skills, making learning fun and interactive!
Understanding Fractions

Before we dive into comparing fractions, let’s establish a basic understanding:
- Numerator: The top number in a fraction, which tells us how many parts we have.
- Denominator: The bottom number, indicating the total number of parts the whole is divided into.
Here’s an image to visualize these components:

Tip 1: Compare Fractions with the Same Denominator

When fractions have the same denominator, comparison becomes straightforward because you’re essentially comparing the number of parts:
- Consider the fractions 3⁄8 and 5⁄8.
- The denominator is 8 for both, so we compare the numerators: 3 vs. 5.
- 5 is larger than 3, thus 5⁄8 is greater than 3⁄8.

Tip 2: Compare Fractions with the Same Numerator

If numerators are identical, the fraction with the smaller denominator is larger because each part represents a larger portion of the whole:
- Comparing 1⁄2 and 1⁄4.
- Since both have a numerator of 1, compare the denominators: 2 vs. 4.
- 2 is less than 4, so 1⁄2 is greater than 1⁄4.

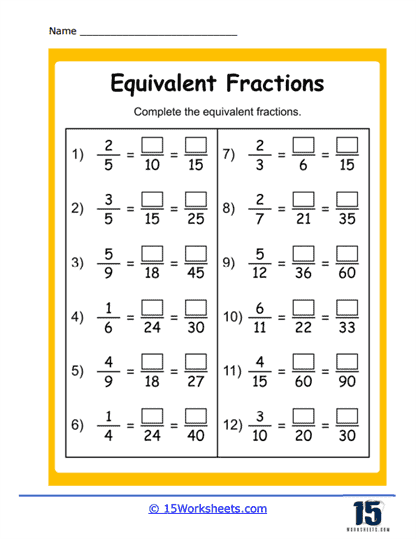
Tip 3: Convert Fractions to Equivalent Fractions

When denominators differ, we need to find a common denominator to compare:
- To compare 2⁄5 and 3⁄10, find the least common multiple (LCM) of 5 and 10, which is 10.
- Convert 2⁄5 to 4⁄10 (since 2⁄5 = (2 x 2)/(5 x 2) = 4⁄10).
- Now compare 4⁄10 to 3⁄10; since 4 is greater than 3, 2⁄5 is greater than 3⁄10.
⚠️ Note: The common denominator method works with any type of fraction, making it a versatile approach.
Tip 4: Cross-Multiplying
When converting fractions feels cumbersome, cross-multiplying can be a faster alternative:
- When comparing 2⁄3 and 3⁄4, cross-multiply as follows:
- 2 x 4 (top numerator x bottom denominator) and 3 x 3 (bottom numerator x top denominator).
- The results are 8 and 9. Since 9 is greater, 3⁄4 is greater than 2⁄3.
Tip 5: Use a Visual Approach

Visual aids can provide intuitive comparisons:
- Using bar models or pie charts, compare the fractions 3⁄4 and 5⁄8.
- Draw and shade 3⁄4 of one bar and 5⁄8 of another.
- From the visual representation, it’s clear that 3⁄4 occupies more space than 5⁄8.
Here’s how you could illustrate this comparison:

In summary, by following these five tips, you can confidently compare fractions:
- Using the same denominator or numerator simplifies comparison.
- Converting to equivalent fractions is reliable but can be time-consuming.
- Cross-multiplying offers a quicker method.
- Visual aids can make complex comparisons easier to grasp.
To help you practice these tips, we've prepared a free worksheet with exercises tailored to reinforce these techniques. Happy learning!
Why is it important to compare fractions?

+
Comparing fractions allows us to understand and use them effectively in real-life scenarios like measurements, financial calculations, and cooking, enhancing our mathematical literacy.
What’s the easiest way to compare fractions if the denominators are different?

+
Finding a common denominator or using visual aids might be the easiest ways, depending on your comfort level with the methods. Common denominators are more precise but visual comparisons can be faster for estimation.
Can fractions be compared without converting them?

+
Yes, you can compare fractions by cross-multiplying or by using visual representations, both of which provide a quick way to compare without conversion.
Related Terms:
- Comparing fractions worksheet free pdf
- Comparing fractions Worksheet with answers
- Comparing fractions Worksheet grade 4
- Comparing fractions Worksheet Grade 5