Comparing Fractions With Models Worksheet: Fun for Kids

If you're on the journey of teaching your kids how to understand and compare fractions, you've come to the right place. Understanding fractions is a fundamental math skill that lays the groundwork for more complex mathematical operations. While traditional methods have their place, bringing in a bit of creativity can make learning fractions a fun and engaging experience. Here’s how we can use models to compare fractions through a specially designed worksheet that’s enjoyable for kids.
Why Models Work for Teaching Fractions

Before diving into the worksheet, let’s explore why models are an excellent tool for teaching fractions:
- Visual Appeal: Kids are visual learners; models allow them to see what fractions represent.
- Concrete Understanding: Models make abstract numbers tangible, giving children something they can touch and manipulate.
- Engagement: It turns learning into a game, keeping children interested and involved.
Using models like fraction strips, pie charts, or fraction circles not only helps in visualizing the fractions but also in understanding their relative sizes.
Setting Up the Worksheet

Here’s how you can set up an engaging worksheet for comparing fractions using models:
Materials Needed

- Paper or a worksheet
- Fraction models (fraction strips, pie charts, etc.)
- Markers, crayons, or colored pencils
- A positive attitude!
Steps to Create the Worksheet

- Choose Your Models: Decide which type of models you’ll use for this activity. Popular options include:
- Fraction strips - great for linear comparison.
- Pie charts or circle models - excellent for part-to-whole relationships.
- Area models - can be used to show fractions as parts of a whole.
<li><strong>Design the Layout:</strong> Divide your worksheet into sections. Each section can have a problem where children need to compare two or more fractions using models.
<table>
<tr>
<th>Problem</th>
<th>Fractions</th>
<th>Model</th>
</tr>
<tr>
<td>Problem 1</td>
<td>1/2, 1/4</td>
<td>Fraction Strips</td>
</tr>
<tr>
<td>Problem 2</td>
<td>3/4, 2/3</td>
<td>Pie Chart</td>
</tr>
<tr>
<td>Problem 3</td>
<td>5/8, 3/5</td>
<td>Area Model</td>
</tr>
</table>
</li>
<li><strong>Instructions:</strong> Provide clear instructions for each problem. For example, "Color in the fractions on the pie chart and circle which fraction is larger."</li>
⚠️ Note: Make sure the models you choose are appropriate for the level of the student. For younger learners, use simple fractions; for older kids, you can include more complex comparisons.
Engaging with the Worksheet

Now that your worksheet is ready, here’s how to make the experience engaging:
Color Coding

Use different colors to represent different fractions. This not only makes the worksheet visually appealing but also aids in distinguishing between fractions easily.
Turn It Into a Game

Make comparisons competitive by turning the worksheet into a race or a treasure hunt. Kids could compete to see who can identify the larger fraction the fastest.
Practical Application

Encourage children to create their own models using everyday objects like slices of pizza, apples, or pieces of paper. This can help bridge the gap between theoretical and practical understanding.
Group Activity

Working in pairs or small groups can facilitate discussion and peer learning. Each child could be responsible for a part of the problem, promoting collaboration and teamwork.
Final Thoughts
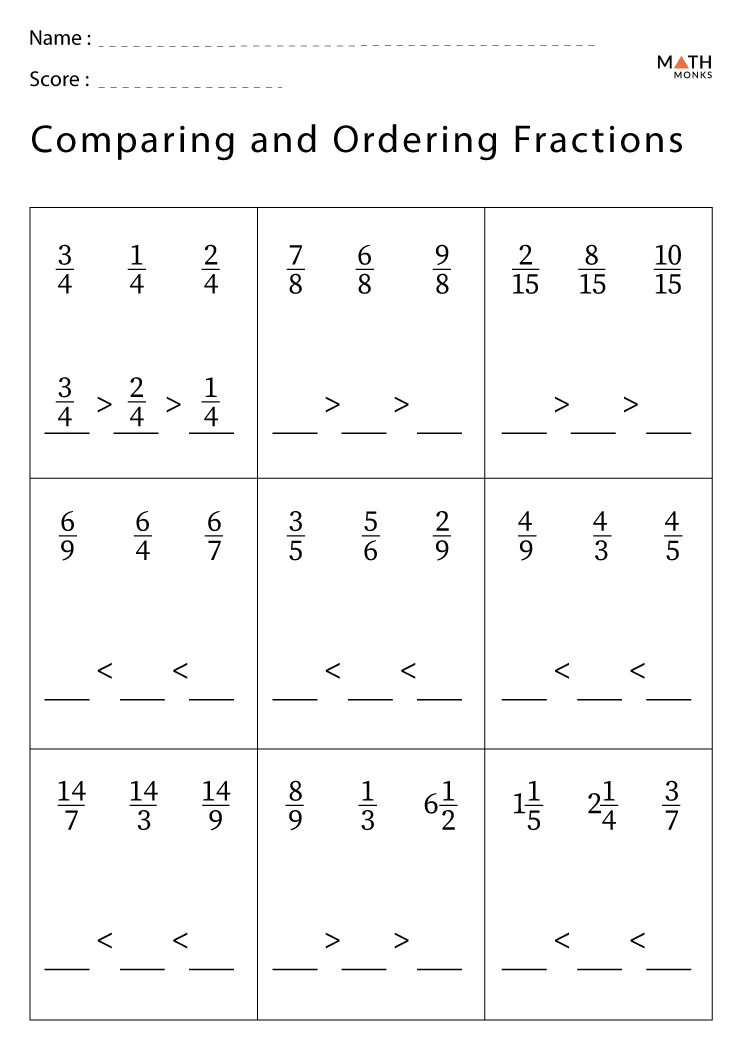
Using models in a comparing fractions worksheet not only simplifies the concept for kids but also embeds a sense of fun in learning. Through this approach, children can physically see the differences between fractions, which fosters a deeper understanding of how numbers relate to each other. The worksheet becomes more than just an academic tool; it’s a playground for curiosity, exploration, and learning. It’s about making math less intimidating and more accessible, allowing children to confidently tackle more complex problems as they grow.
Why are models better than traditional methods for teaching fractions?

+
Models provide a visual representation, which helps children who are visual or kinesthetic learners understand the concept of fractions more intuitively than numerical equations alone.
How can I make sure the models are age-appropriate for my students?

+
Consider the complexity of the fractions. Younger students might benefit from halves, thirds, and quarters, while older students can handle more intricate comparisons like sevenths and ninths.
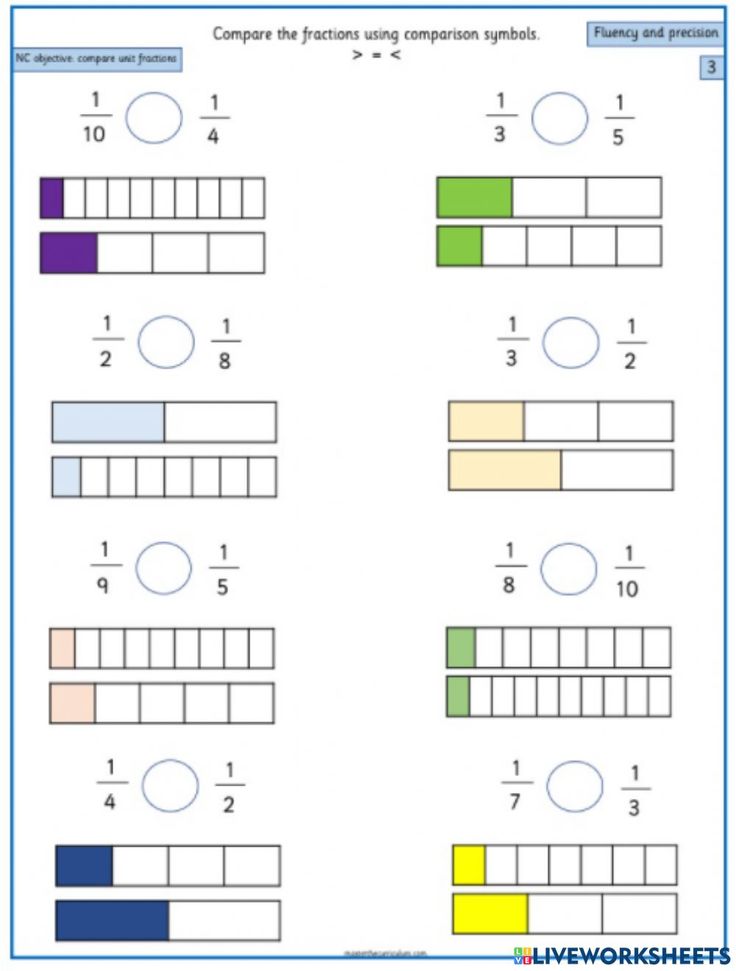
What are some common mistakes to avoid when using models to teach fractions?
+
Avoid using models where the visual representation might mislead; for example, don’t use pie charts for comparing fractions with different denominators if the sizes of the charts differ.
Related Terms:
- Comparing fractions Worksheet with answers
- Comparing fractions Worksheet PDF