Compare Fractions With Different Denominators

Introduction to Comparing Fractions

When dealing with fractions, it’s essential to understand how to compare them, especially when they have different denominators. Fractions are a way to represent a part of a whole, and comparing them is crucial in various mathematical operations. In this article, we will delve into the world of fractions and explore how to compare them when they have different denominators.
Understanding Fractions

Before we dive into comparing fractions, let’s first understand what fractions are. A fraction is a way to represent a part of a whole. It consists of two parts: the numerator and the denominator. The numerator represents the number of equal parts we have, while the denominator represents the total number of parts the whole is divided into. For example, in the fraction 3⁄4, the numerator is 3, and the denominator is 4.
Why Compare Fractions?

Comparing fractions is essential in various mathematical operations, such as adding, subtracting, multiplying, and dividing. When we compare fractions, we can determine which one is larger or smaller. This is particularly useful when dealing with real-world problems, such as measuring ingredients for a recipe or calculating the cost of materials for a project.
Comparing Fractions with Different Denominators

When comparing fractions with different denominators, we need to find a common denominator. A common denominator is a denominator that both fractions can share. To find a common denominator, we can use the following steps: * List the multiples of each denominator * Find the smallest multiple that both denominators share * Convert both fractions to have the common denominator
For example, let’s compare the fractions 1⁄2 and 1⁄3. To compare them, we need to find a common denominator. The multiples of 2 are 2, 4, 6, 8, 10,…, and the multiples of 3 are 3, 6, 9, 12, 15,…. The smallest multiple that both denominators share is 6. Therefore, the common denominator is 6.
Converting Fractions to Have a Common Denominator

Once we have found the common denominator, we can convert both fractions to have that denominator. To convert a fraction, we multiply the numerator and denominator by the same number. For example, to convert the fraction 1⁄2 to have a denominator of 6, we multiply the numerator and denominator by 3: 1⁄2 = (1 x 3) / (2 x 3) = 3⁄6
Similarly, to convert the fraction 1⁄3 to have a denominator of 6, we multiply the numerator and denominator by 2: 1⁄3 = (1 x 2) / (3 x 2) = 2⁄6
Now that both fractions have the same denominator, we can compare them: 3⁄6 > 2⁄6
Therefore, the fraction 1⁄2 is greater than the fraction 1⁄3.
Using a Table to Compare Fractions
We can use a table to compare fractions with different denominators. The table below shows the fractions 1⁄2, 1⁄3, and 2⁄3, along with their equivalent fractions with a common denominator of 6:
| Fraction | Equivalent Fraction |
|---|---|
| 1/2 | 3/6 |
| 1/3 | 2/6 |
| 2/3 | 4/6 |

By using a table, we can easily compare fractions with different denominators and determine which one is larger or smaller.
📝 Note: When comparing fractions, it's essential to find a common denominator to ensure accurate results.
Real-World Applications of Comparing Fractions
Comparing fractions has numerous real-world applications. For example, in cooking, we often need to measure ingredients in fractions. When comparing fractions, we can determine which ingredient is more or less than another. In construction, we may need to compare the cost of materials, which can be represented as fractions. By comparing fractions, we can determine which material is more cost-effective.
In conclusion, comparing fractions with different denominators is a crucial mathematical operation that has numerous real-world applications. By finding a common denominator and converting fractions, we can accurately compare them and determine which one is larger or smaller. Whether we’re measuring ingredients for a recipe or calculating the cost of materials for a project, comparing fractions is an essential skill that can help us make informed decisions.
What is a common denominator?

+
A common denominator is a denominator that both fractions can share. It’s the smallest multiple that both denominators have in common.
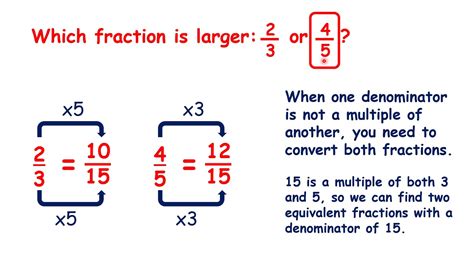
How do I convert a fraction to have a common denominator?
+
To convert a fraction, multiply the numerator and denominator by the same number. This will give you an equivalent fraction with the common denominator.
Why is comparing fractions important?

+
Comparing fractions is important because it allows us to determine which fraction is larger or smaller. This is useful in various mathematical operations, such as adding, subtracting, multiplying, and dividing, and has numerous real-world applications.


