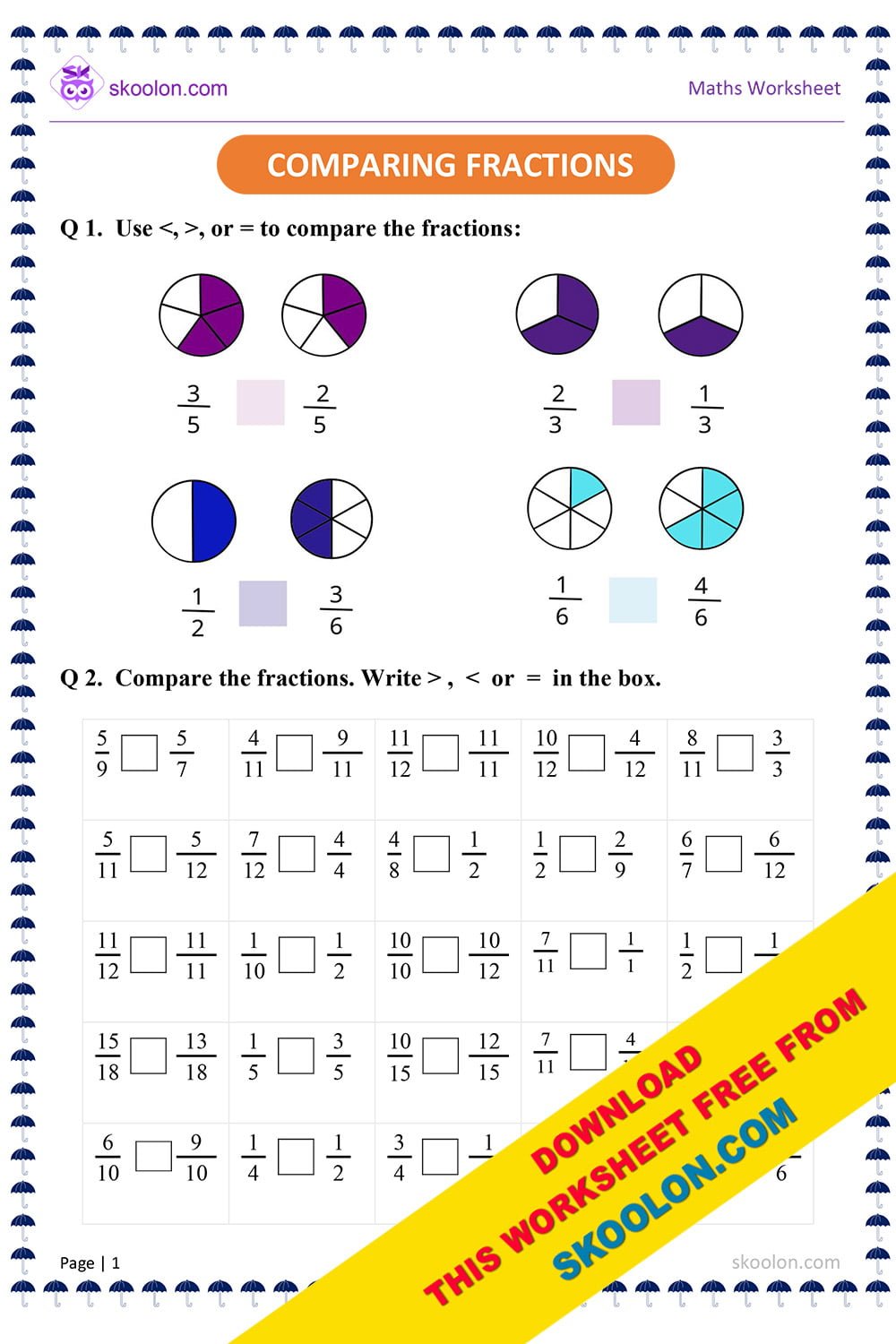
5 Ways Compare Fractions

Introduction to Comparing Fractions
Comparing fractions is a fundamental concept in mathematics that involves determining which of two fractions is larger or smaller. This can be achieved through various methods, each with its own advantages and applications. Understanding how to compare fractions is essential for solving problems in algebra, geometry, and other branches of mathematics. In this article, we will delve into five ways to compare fractions, exploring their step-by-step processes and providing examples to illustrate each method.
Method 1: Finding a Common Denominator
One of the most straightforward ways to compare fractions is by finding a common denominator. This involves converting both fractions so that they have the same denominator, making it easy to compare their numerators. The steps are as follows: - Identify the denominators of the two fractions. - Find the least common multiple (LCM) of these denominators. - Convert both fractions to have the LCM as their new denominator. - Compare the numerators; the fraction with the larger numerator is the larger fraction.
For example, to compare 1⁄4 and 1⁄6, we find the LCM of 4 and 6, which is 12. We then convert both fractions: (1⁄4) becomes (3⁄12) and (1⁄6) becomes (2⁄12). Since 3 is greater than 2, 1⁄4 is larger than 1⁄6.
Method 2: Cross Multiplication
Another method for comparing fractions is cross multiplication, also known as cross multiplying. This technique is useful when finding a common denominator is cumbersome. The process involves: - Multiplying the numerator of the first fraction by the denominator of the second fraction. - Multiplying the numerator of the second fraction by the denominator of the first fraction. - Comparing the products; the fraction with the larger product is the larger fraction.
For instance, to compare 2⁄3 and 3⁄4 using cross multiplication: - (2 * 4) = 8 - (3 * 3) = 9 Since 9 is greater than 8, 3⁄4 is larger than 2⁄3.
Method 3: Converting to Decimals

Converting fractions to decimals is a practical method for comparison, especially when dealing with fractions that have large or complex denominators. The steps are: - Divide the numerator by the denominator for each fraction to get their decimal equivalents. - Compare the decimals; the larger decimal corresponds to the larger fraction.
To compare 3⁄8 and 2⁄5: - 3⁄8 = 0.375 - 2⁄5 = 0.4 Since 0.4 is greater than 0.375, 2⁄5 is larger than 3⁄8.
Method 4: Comparing Fractions with the Same Numerator

When fractions have the same numerator but different denominators, the comparison is straightforward: - The fraction with the smaller denominator is the larger fraction.
For example, comparing 4⁄5 and 4⁄7: - Since 5 is less than 7, 4⁄5 is larger than 4⁄7.
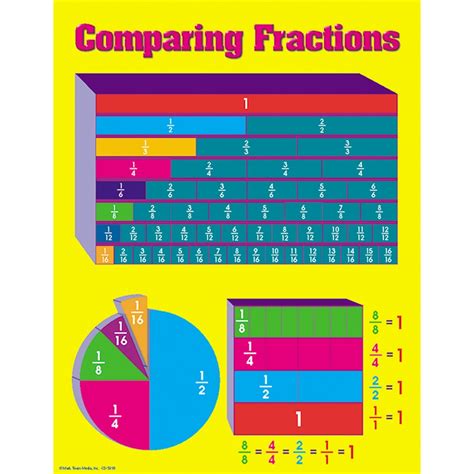
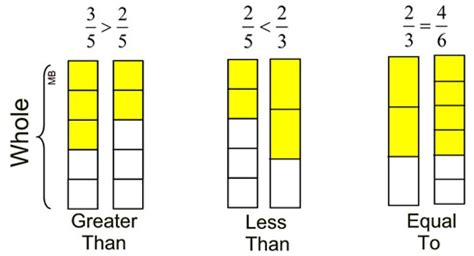
Method 5: Using Fraction Comparison Tools or Charts
For a more visual approach, fraction comparison charts or tools can be utilized. These resources provide a quick way to compare fractions by plotting them on a number line or using pre-calculated charts. However, this method may not be as commonly used or as straightforward as the others, especially for those who prefer algebraic or arithmetic solutions.
📝 Note: While visual tools can be helpful for an initial understanding, mastering the arithmetic methods (like finding a common denominator or cross multiplication) provides a deeper mathematical insight and is usually more efficient for complex problems.
To summarize, comparing fractions can be achieved through multiple methods, each with its unique approach and application. Whether it’s finding a common denominator, cross multiplying, converting to decimals, comparing fractions with the same numerator, or using visual tools, understanding these methods enhances one’s ability to solve mathematical problems with precision and confidence.
In the realm of mathematics, being adept at comparing fractions opens doors to more complex mathematical concepts and problem-solving strategies. It’s a fundamental skill that, once mastered, can significantly enhance one’s mathematical prowess and analytical thinking.
What is the easiest way to compare fractions?

+
The easiest way often involves finding a common denominator or converting fractions to decimals, as these methods are straightforward and easy to understand.
Why is comparing fractions important?
+
Comparing fractions is crucial for problem-solving in various mathematical disciplines, including algebra and geometry. It also enhances analytical and critical thinking skills.
Can fractions be compared without finding a common denominator?

+
Yes, fractions can be compared without finding a common denominator by using methods such as cross multiplication or converting fractions to decimals.



