Mastering Fraction Comparisons: Worksheet Wonders for Learning

Mastering Fraction Comparisons
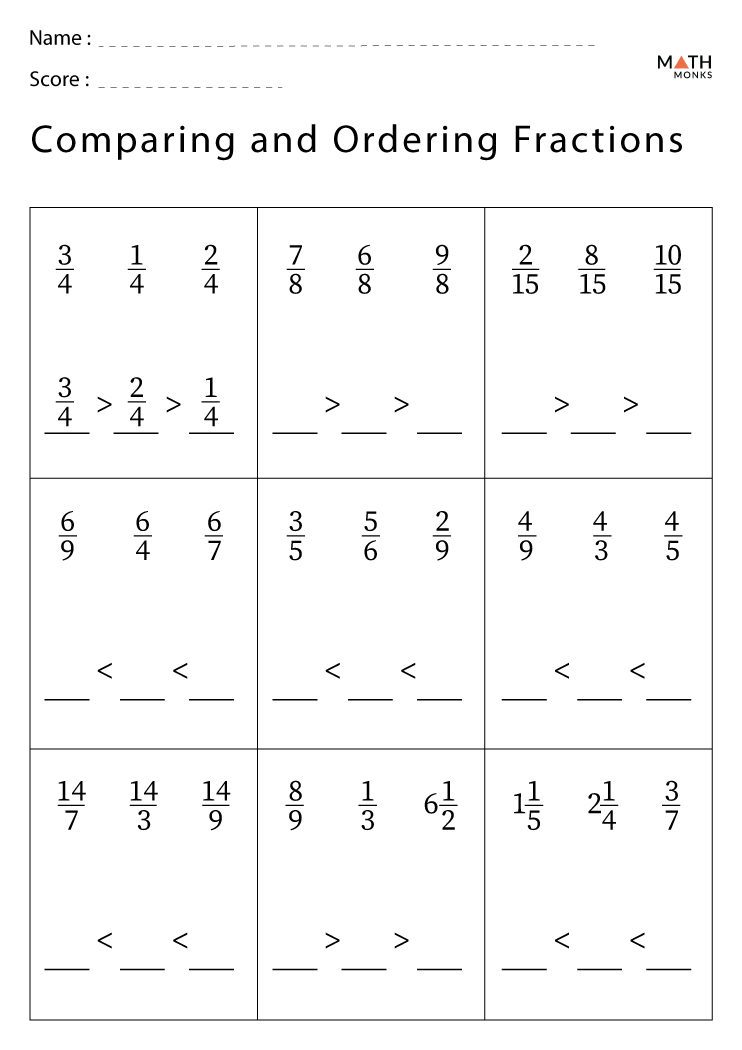
Fractions can be an intimidating topic for many students, especially when it comes to comparison. Understanding how to compare fractions lays a solid foundation for all future mathematics endeavors, including algebra and beyond. In this comprehensive guide, we’ll explore various methods to teach and practice fraction comparison through engaging worksheets, ensuring that the learning process is not only educational but also enjoyable.
The Basics of Fractions

Fractions consist of a numerator (the number above the line) and a denominator (the number below the line), representing a part of a whole. Here are some key aspects:
- Like Fractions: Have the same denominator.
- Unlike Fractions: Have different denominators.
- Proper Fractions: Where the numerator is smaller than the denominator.
- Improper Fractions: Where the numerator is equal to or greater than the denominator.
🍏 Note: Understanding the relationship between the numerator and the denominator is crucial for comparing fractions effectively.
Why Compare Fractions?

Comparison is essential for various mathematical operations like addition, subtraction, and even understanding ratios and proportions. It helps in:
- Making sense of proportions in real-life scenarios, like cooking or carpentry.
- Solving problems where quantities need to be understood relative to one another.
- Forming the basis for advanced algebraic concepts.
Worksheet Strategies for Comparison

Visual Comparison

Before diving into numerical methods, visual representations can be a powerful tool. Here are some worksheet ideas:
- Draw fractions as parts of a whole (pies, rectangles).
- Compare fractions by shading parts of a grid or bar.
- Use matching games where students pair equivalent fractions or compare fractions visually.

Converting to Like Denominators

The most common technique involves converting fractions to have like denominators, allowing direct comparison:
- Find the Least Common Denominator (LCD): The smallest number that both denominators can divide into.
- Convert: Multiply the numerator and denominator by the same number to get equivalent fractions with the LCD.
📘 Note: Always simplify fractions after conversion to keep them manageable for students.
Comparing to One-Half

A more intuitive method for some students is to compare fractions to one-half:
- If the numerator is less than half of the denominator, the fraction is less than one-half.
- If greater, then the fraction is more than one-half.
- Use this benchmark to compare two fractions by determining which is closer or further from one-half.
Worksheet Design Tips

Here are some considerations to keep worksheets effective and engaging:
- Use progressive difficulty levels to gradually increase challenge.
- Incorporate real-life scenarios to show practical applications.
- Encourage self-checking through cross-referencing or visual clues.
- Include games and puzzles to make learning fun.
| Type of Worksheet | Goals |
|---|---|
| Basic Comparison | Simple like-fraction comparisons using visual aids or one-half benchmark. |
| Advanced Comparison | Using LCD or cross-multiplying, comparing mixed numbers, or comparing fractions with different denominators. |
| Conceptual | Understanding place in number lines or through real-life scenario analysis. |

Using Worksheets for Assessment

Worksheets can serve as an excellent assessment tool:
- Track progress over time by revisiting earlier worksheets with slight modifications.
- Use worksheets for both formative and summative assessments, adjusting complexity accordingly.
Wrapping Up

Throughout this guide, we’ve explored how worksheets can become dynamic tools for teaching fraction comparisons. By blending visual methods with numerical techniques, educators can cater to different learning styles, ensuring students grasp this fundamental mathematical skill. From basic comparisons to advanced strategies, the key is to keep the learning process interactive and relatable. With practice and the right approach, students can demystify fractions and unlock the potential they hold for more complex math concepts.
Why are fraction comparisons important?

+
Fraction comparisons are crucial for understanding ratios, proportions, and performing basic arithmetic operations like addition and subtraction of fractions. They also form the foundation for algebraic concepts and problem-solving in various real-life scenarios.
How can I help students who struggle with comparing fractions?

+
Use visual aids to make abstract concepts concrete. Encourage practice through fun worksheets, games, and real-life applications. Breaking down the steps into smaller, manageable parts can also help students who find comparison challenging.
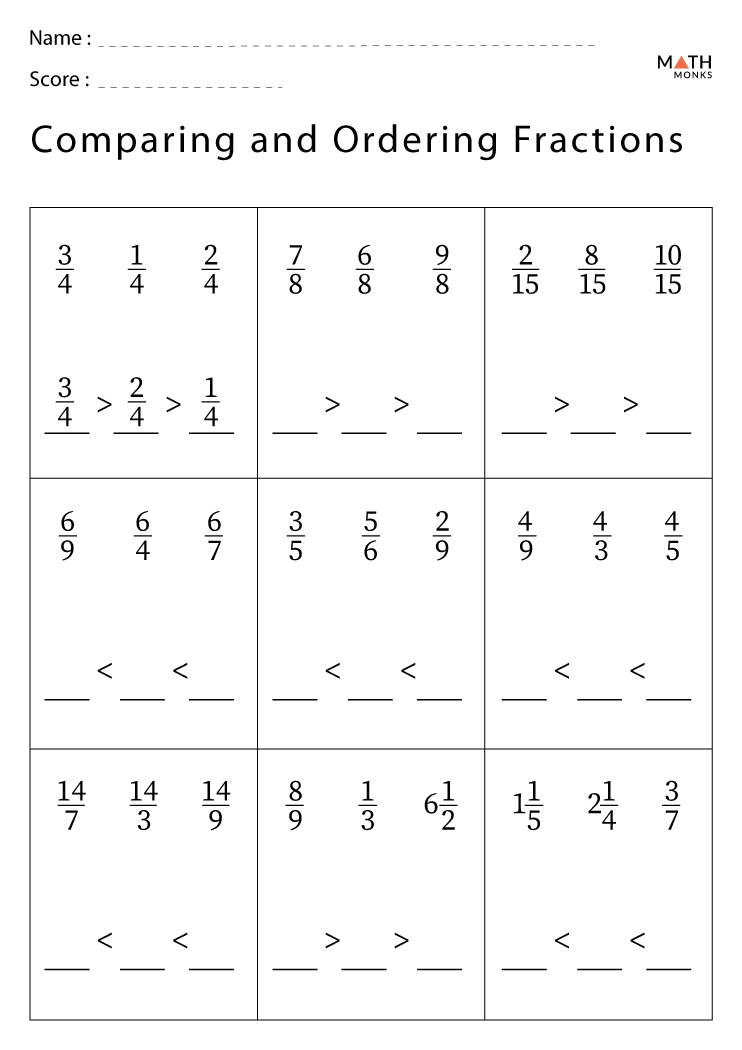
What are some common mistakes students make when comparing fractions?
+
Students often mistake comparing numerators or denominators independently, overlook finding the least common denominator, or forget to convert improper fractions to mixed numbers before comparison. Ensuring they understand the importance of context and equivalence can help avoid these pitfalls.