5 Ways to Compare Proportional Relationships Effectively

Understanding proportional relationships is fundamental across various disciplines, especially in mathematics and science. Whether you're a student tackling algebra, a business analyst evaluating data, or a cook adjusting recipes, knowing how to compare proportional relationships effectively can be incredibly beneficial. This blog post will explore five methods to do just that, ensuring accuracy and clarity in your assessments.
Graphical Analysis
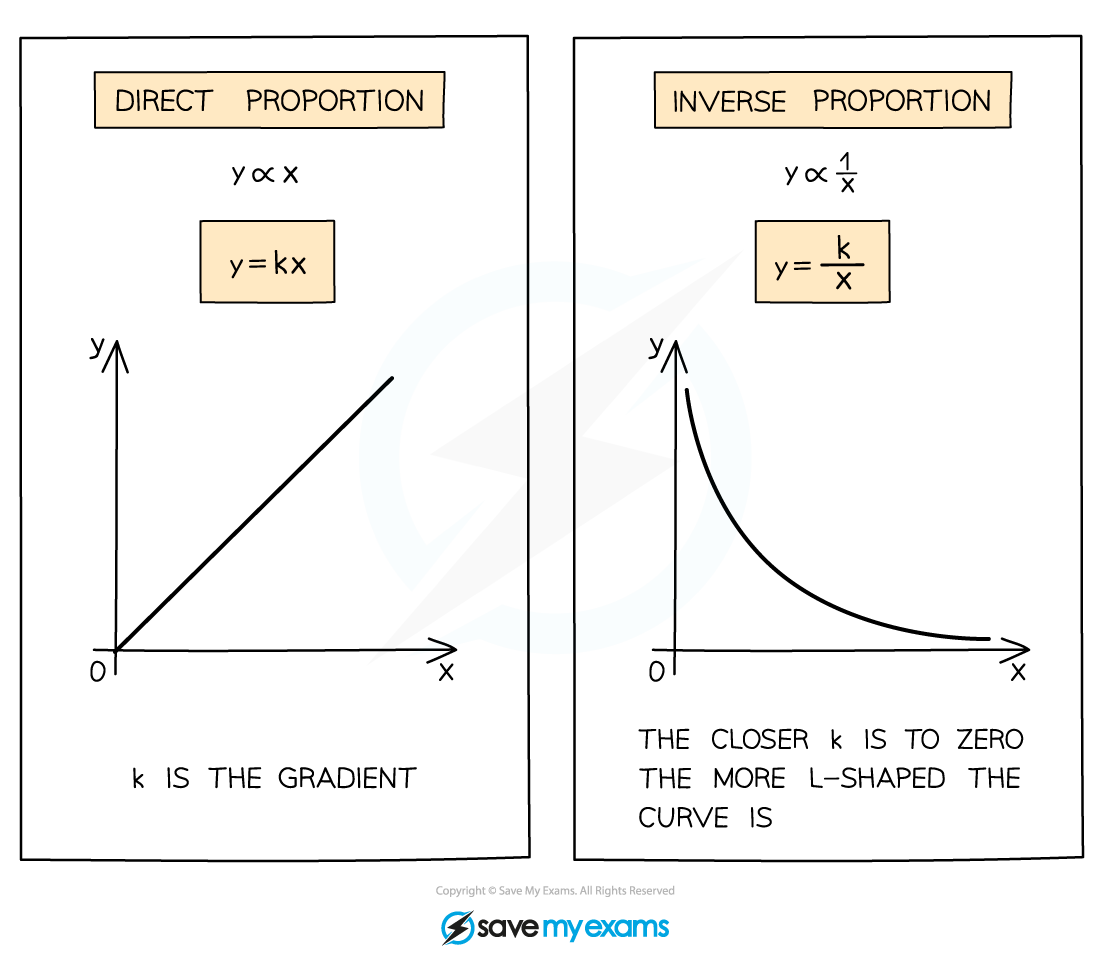

The first method involves visual representation through graphs. Here are some key points for effective graphical analysis:
- Line Graphs: Plot the quantities against each other or against a third variable if applicable. A straight line through the origin often indicates a direct proportional relationship.
- Slope: The slope of the line in a linear graph represents the constant of proportionality (k). Different relationships can be compared by examining the steepness or slope of their respective lines.
- Intercept: Ensure the lines pass through the origin. If they do not, the relationship might not be proportional or the data could be incorrect.
✅ Note: When comparing multiple sets of data, use the same scale on the axes for accurate comparison.
Setting Up Ratios

Another straightforward method is comparing ratios directly:
- Find the ratio of each set of data or variables.
- Compare these ratios. If the ratios are equal, the relationships are proportional. For example, if y=kx, then y/x=k for all data points.
| Variable | Value 1 | Value 2 | Ratio |
|---|---|---|---|
| Y | 40 | 60 | 20 |
| X | 2 | 3 | 20 |

✅ Note: Remember to check consistency in units when comparing ratios.
Unit Rate Analysis

When dealing with rates such as speed, cost, or production, unit rates provide a clear comparison:
- Calculate the unit rate for each proportional relationship.
- Compare these rates to determine the efficiency or effectiveness of each relationship.
For example, if a car travels 90 miles in 2 hours, its unit rate or speed is 45 mph (miles per hour).
Direct and Inverse Proportions

Proportional relationships can be either direct or inverse. Here’s how to distinguish:
- Direct Proportion: As one quantity increases, the other increases or decreases at the same rate.
- Inverse Proportion: As one quantity increases, the other decreases in a manner that their product remains constant.
🔍 Note: When comparing these, ensure you’ve correctly identified the nature of the relationship to avoid misinterpretation.
Using Cross Multiplication for Equations

If you have equations for each relationship:
- Set up proportion equations and solve by cross multiplication.
- Compare the results to determine if they align with proportionality.
E.g., for relationships of y = kx and y’ = k’x’, cross-multiplying would show if k = k’.
By employing these five techniques, you can ensure that you're comparing proportional relationships with precision and understanding. Each method has its strengths, and choosing the right one can depend on the context and the data available. For example, graphical methods are excellent for visual learners, while setting up ratios might be more straightforward in numerical analyses.
Ultimately, mastering these methods enhances your ability to interpret data, make predictions, and solve problems across various fields. Whether you're analyzing data in a lab, predicting future trends, or simply trying to scale a recipe, understanding and comparing proportional relationships opens up a world of logical and quantitative analysis. Keep in mind that the beauty of math lies not just in numbers but in the patterns and relationships they reveal, helping us to better understand and interact with the world around us.
What if my data doesn’t follow a straight line?

+
If the data does not form a straight line, it might not be directly proportional. Consider checking for an indirect or inverse relationship or if there are other influencing factors at play.
Can these methods work for non-linear relationships?

+
The methods discussed are primarily for linear or proportional relationships. However, some can be adapted for non-linear situations, especially when understanding growth patterns or rates.
How do I know if my data is proportional?

+
Check if the ratio of the dependent variable to the independent variable remains constant. If this ratio is consistent across all data points, then the relationship is likely proportional.