Unlocking the Mystery of Combined Volume for 5th Graders
Understanding volume in math can be a perplexing concept for students in the 5th grade, especially when they first encounter it. However, with the right approach, it can become an exciting adventure of exploration into geometry, leading them to comprehend how different shapes combine to form larger structures. This post will guide young learners through the essentials of combined volume and offer practical exercises to solidify their understanding.
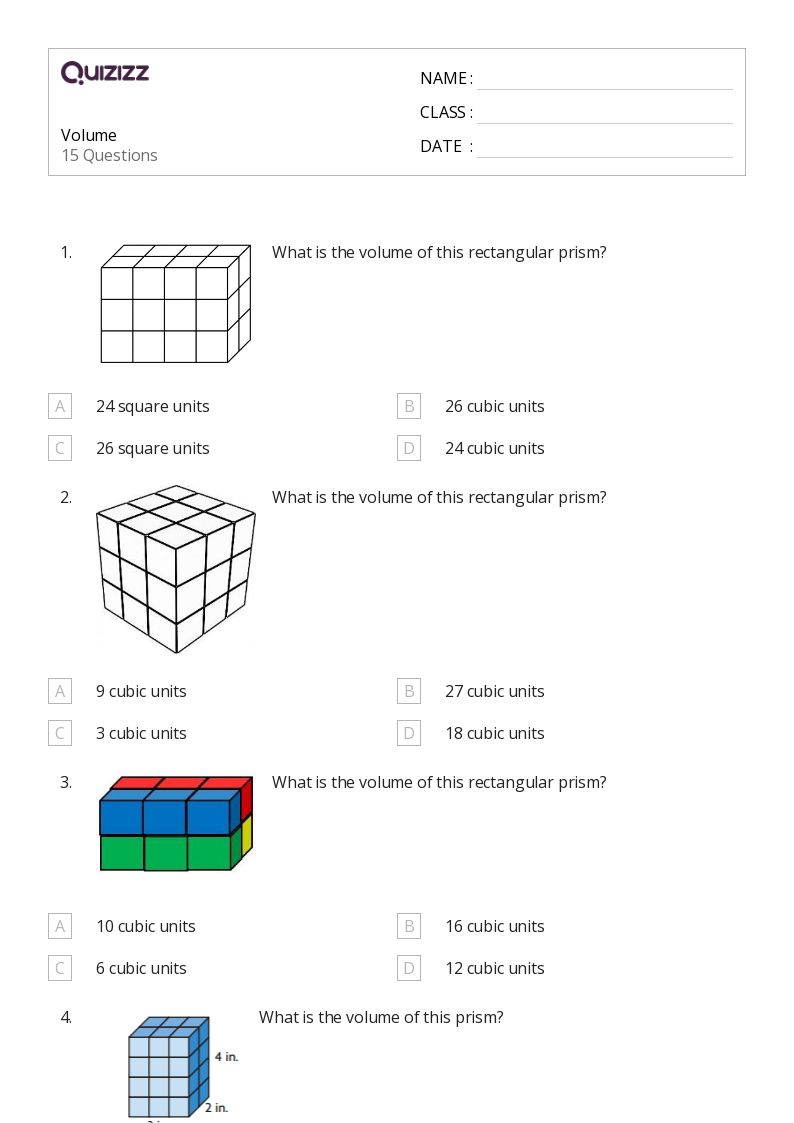
The Concept of Volume

Volume is the amount of space an object occupies in three dimensions, usually measured in cubic units. For 5th graders, introducing this as the space inside a box or room can make it more relatable:
- Think of volume as how many cubes you can fit inside a shape.
- Different shapes like cubes, rectangular prisms, and even more complex polyhedrons have unique formulas to calculate their volume.
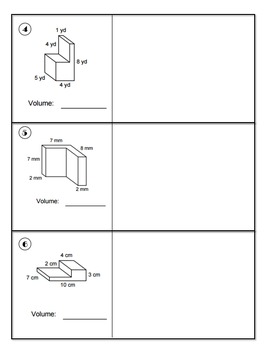
Combined Volume: Putting Shapes Together

When we talk about combined volume, we are looking at how volumes add up when we join different shapes. Here’s how to approach it:
- First, identify the individual shapes within the structure.
- Calculate the volume of each shape separately.
- Finally, add these volumes together to get the total volume.
Step-by-Step Guide to Calculate Combined Volume

Let’s break down the process:
- Identify the Shapes: Look at the complex object and identify smaller, simpler shapes it’s made of. For instance, a building might be a rectangular prism on top of a cylinder.
- Calculate Each Volume:
- Rectangular Prism: Use the formula (V = l \times w \times h).
- Cylinder: Use (V = \pi r^2 h), where (r) is the radius of the base, and (h) is the height.
- Pyramid: Use (V = \frac{1}{3} \times \text{Base Area} \times h).
- Sum the Volumes: Once you have the volumes, add them up to get the total volume.
Practical Exercises for 5th Graders

Here are some activities to practice calculating combined volumes:
- Building Block Puzzle: Provide students with interlocking building blocks. Ask them to create shapes and calculate the combined volumes.
- Sand or Water Measurement: Use small containers and measure the volume of sand or water they can hold, then combine different containers to understand volume addition.
- Drawing and Estimation: Sketch different combinations of 3D shapes and have students estimate and then calculate their total volume.
🧠 Note: Ensure that the blocks or materials used are appropriately sized for children’s hands and safety.
Using Math in Real Life

Connect these volume calculations to real-life scenarios:
| Shape | Real-Life Example | Volume Calculation |
|---|---|---|
| Rectangular Prism | A box or room | (V = l \times w \times h) |
| Cylinder | A can of soup | (V = \pi r^2 h) |
| Pyramid | A tent | (V = \frac{1}{3} \times \text{Base Area} \times h) |
Tips for Teaching Combined Volume to 5th Graders

Educating kids on combined volume requires patience and creativity. Here are some strategies:
- Use visual aids like 3D models or dynamic software to demonstrate how shapes fit together.
- Encourage collaborative learning, allowing students to work in pairs or small groups to solve volume problems.
- Make it fun with volume games or puzzles that involve stacking blocks or arranging different shapes.
When students grasp the concept of combined volume, they open up a world of possibility in understanding how everyday objects are constructed and how spaces can be utilized efficiently. Remember that the process should be engaging, encouraging students to explore, question, and enjoy the process of learning. This foundational knowledge not only helps in math but also fosters critical thinking and problem-solving skills, setting the stage for advanced learning in geometry and spatial relations in the future.
Why is learning about combined volume important for 5th graders?

+
Understanding combined volume helps students develop a spatial awareness that is crucial for solving real-life problems and prepares them for more complex geometry in higher grades.
Can real-life examples be used to teach combined volume?

+
Absolutely, using tangible objects like rooms, packaging boxes, or containers filled with different shapes can illustrate how volumes combine in everyday scenarios.
What are some common mistakes students make when calculating combined volume?

+
One common mistake is forgetting to add the volumes of all shapes together after calculating them individually. Another error is misidentifying the shapes or using incorrect dimensions in the volume formulas.
How can I make learning combined volume interactive and fun?

+
Interactive games, 3D modeling software, or even simple puzzles where students fit different blocks together can make learning this concept engaging and enjoyable.