5 Circular Motion Worksheet Answers You Need

If you're diving into the world of physics or preparing for a physics exam, mastering circular motion is essential. Understanding circular motion can be both challenging and intriguing, but with the right approach, you can excel. Here are five comprehensive answers to common circular motion worksheet questions, ensuring you grasp this fundamental concept:
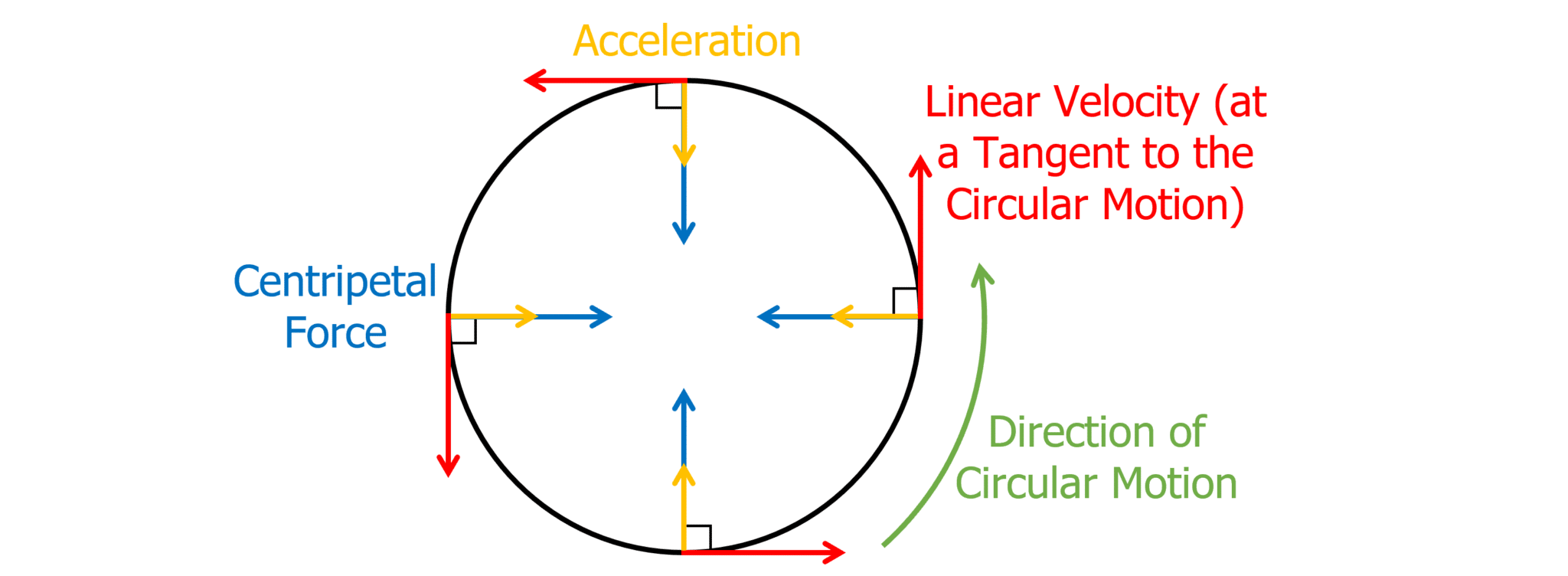
1. Understanding Uniform Circular Motion

Uniform circular motion refers to the motion of an object moving in a circular path at a constant speed. Here are key points to understand:
- Speed vs. Velocity: Although the object’s speed remains constant, its velocity changes due to the changing direction. Velocity is a vector quantity with both magnitude (speed) and direction.
- Acceleration: The acceleration in uniform circular motion points toward the center of the circle and is called centripetal acceleration. The formula for this is (a = \frac{v^2}{r}), where a is the centripetal acceleration, v is the speed, and r is the radius.
- Force: The centripetal force ((F_c)) is the resultant force causing the object to move in a circle. It can be expressed as (F_c = \frac{mv^2}{r}), where m is the mass of the object.
⚠️ Note: Centripetal acceleration and centripetal force are always directed towards the center of the circular path.
2. Application of Newton’s Second Law in Circular Motion

Applying Newton’s second law ((F = ma)) to circular motion involves understanding that the centripetal force must be equal to the product of the mass and the centripetal acceleration:
- Identify the forces acting on the object. For example, tension in a string or gravitational force.
- Resolve these forces into components if necessary. For instance, for a ball on a string swung in a vertical circle, the tension varies at the top and bottom of the path.
Here’s a simple example:
| Position in Circle | Force Equation |
| Top of the Circle | (T + mg = \frac{mv^2}{r}) |
| Bottom of the Circle | (T - mg = \frac{mv^2}{r}) |

🔧 Note: The tension force at different points in a vertical circle varies due to the gravitational force acting on the object.
3. Banked Curves and Friction
On a banked curve, the normal force and the friction force contribute to the centripetal force:
- Angle of Banking: The angle at which a road is tilted to increase the centripetal force and reduce reliance on friction.
- Friction: Friction helps in preventing the car from sliding outward or inward along the curve.
The relationship is:
- (tan(\theta) = \frac{v^2}{rg}) where (v) is velocity, (r) is the radius, and (g) is the acceleration due to gravity.
4. Vertical Loops and Roller Coasters

When analyzing motion in a vertical loop:
- Consider the changing speed due to gravitational potential energy at the top and kinetic energy at the bottom.
- Energy Conservation: At the top of the loop, the kinetic energy plus the potential energy must equal the kinetic energy at the bottom.
5. Non-Uniform Circular Motion

Not all circular motion is at a constant speed. Here are considerations for non-uniform circular motion:
- Total acceleration: It consists of both centripetal acceleration and tangential acceleration due to changes in speed.
- Force components: Apart from the centripetal force, there can be a tangential force causing changes in the object’s speed.
In the end, circular motion offers a fascinating look into how objects interact in space, whether it’s the Moon orbiting Earth, a car navigating a curve, or a roller coaster looping the loop. Grasping these principles not only prepares you for academic assessments but also helps in understanding real-world phenomena where circular motion is at play. Whether you’re tackling a physics problem or simply marveling at the stars, circular motion forms the backbone of many physical interactions.
What’s the difference between centripetal and centrifugal forces?

+
Centripetal force is a real force that points inward, causing an object to follow a curved path. Centrifugal force, often described as the “apparent” outward force, is a pseudo-force observed in a rotating frame of reference.
How can we reduce the friction needed on a banked curve?

+
By increasing the banking angle, you increase the vertical component of the normal force, which acts in the same direction as the centripetal force, thus reducing the reliance on friction.
Can circular motion exist without friction?

+
Yes, for example, a satellite orbits Earth due to gravity alone, and no friction is involved.