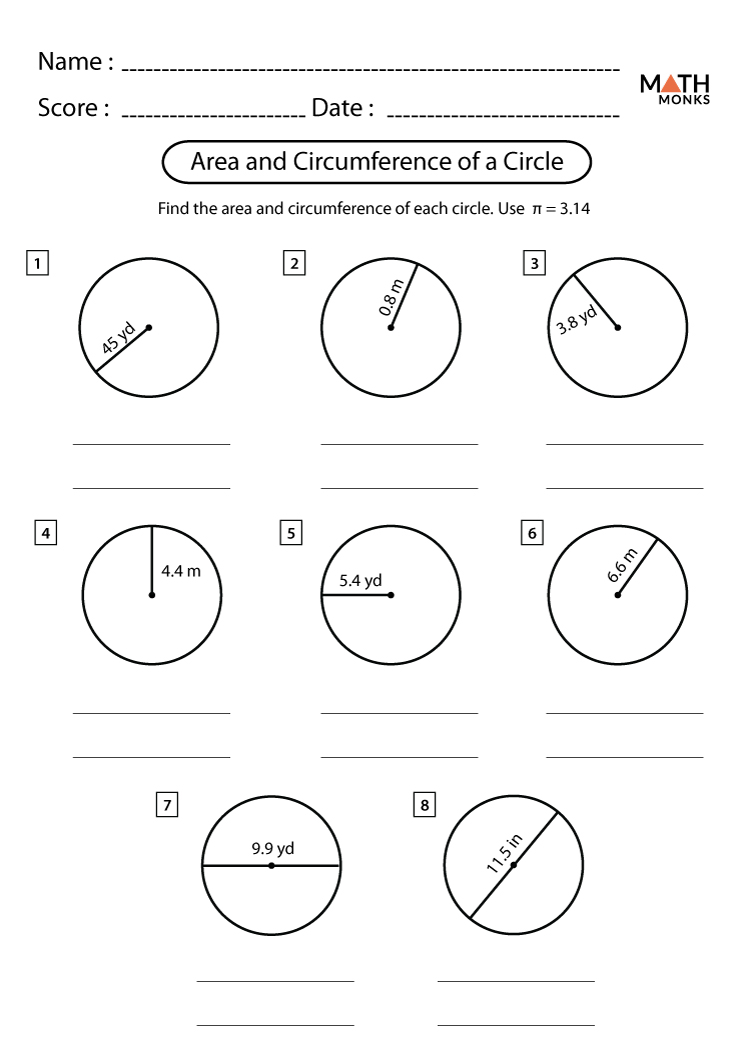
Welcome to our detailed guide on calculating the area of circles, an essential geometry topic for students at various levels of education. Calculating the area of a circle is a fundamental skill in understanding and solving more complex geometric problems. This guide will provide simple solutions and answers for circle area worksheets to help students grasp the concept more confidently.
Understanding the Basics of Circle Area
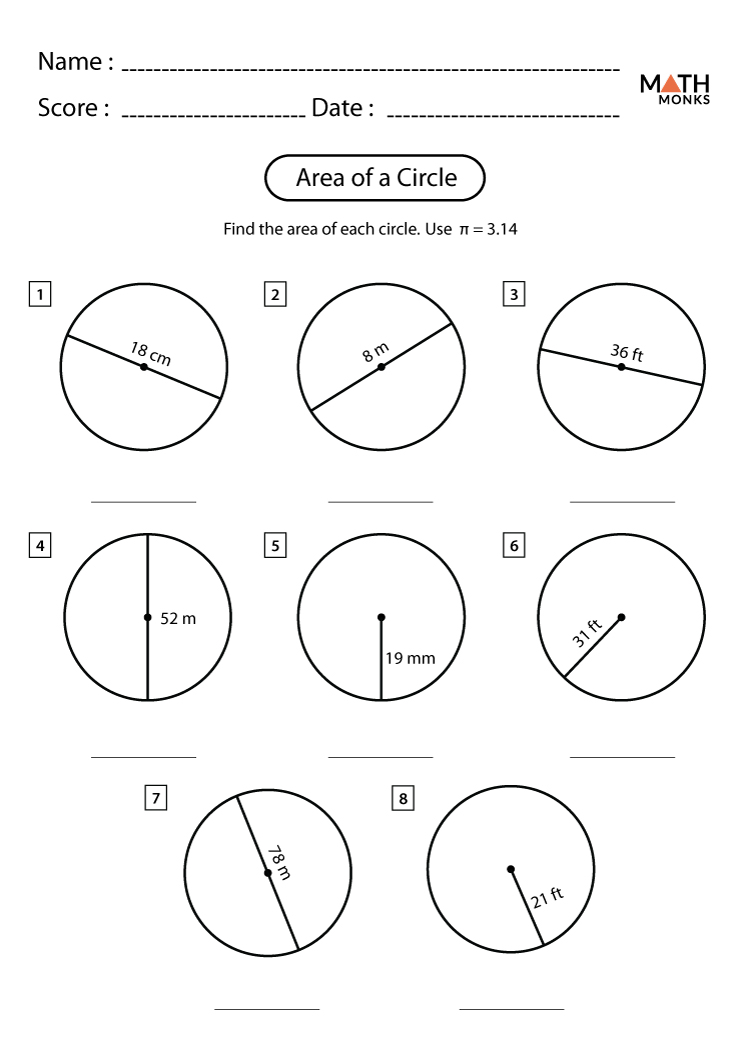
The area of a circle is given by the formula:
[A = \pi \times r^2]
Where:
- A is the area of the circle.
- \pi is the mathematical constant, approximately equal to 3.14159.
- r is the radius of the circle.
⚠️ Note: Be sure to keep track of the units; if the radius is in inches, the area will be in square inches.
Step-by-Step Guide to Find Circle Area
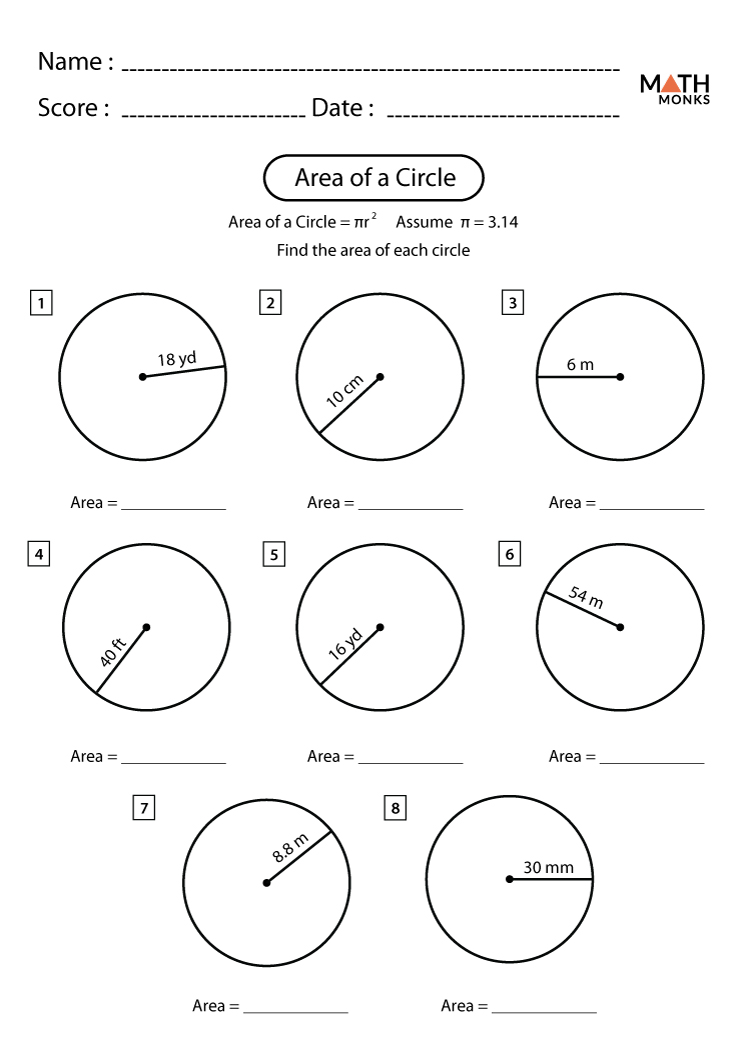
Let’s walk through the steps to find the area of a circle:
- Identify the radius - This is the distance from the center of the circle to any point on its edge.
- Plug the radius into the formula - Square the radius and multiply by π.
- Perform the calculation - Use a calculator if needed to get the exact or approximate value.
- Round your answer - Depending on how precise you need the result, round off to an appropriate number of decimal places.
🔍 Note: When solving circle area problems, it's common to approximate π as 3.14 for simplicity.
Practical Examples with Answers
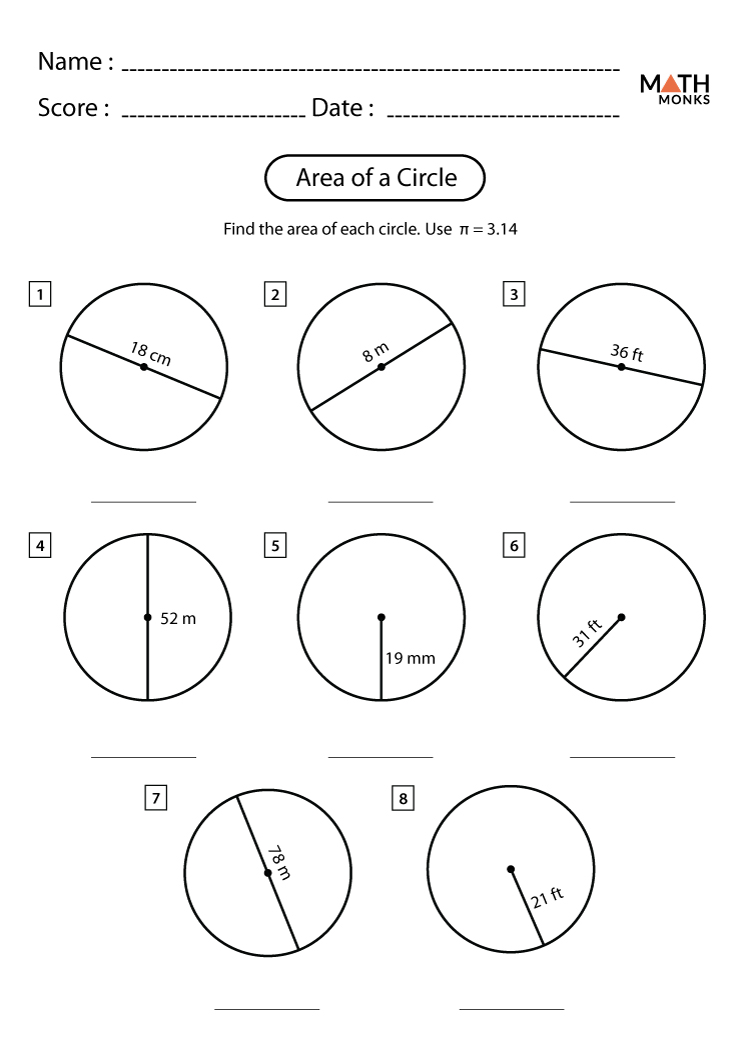
Here are some common worksheet problems with their answers:
Example 1:
Find the area of a circle with a radius of 5 cm.
| Radius (r) | 5 cm |
| Calculation | A = π × (5 cm)2 |
| Area (A) | A ≈ π × 25 cm2 ≈ 78.54 cm2 |
Example 2:
What’s the area of a circle if its diameter is 20 m?
| Diameter (d) | 20 m |
| Radius (r = d/2) | 10 m |
| Calculation | A = π × (10 m)2 |
| Area (A) | A ≈ π × 100 m2 ≈ 314.16 m2 |
Tips for Students
Here are some tips to make calculations easier:
- Memorize the area formula: A = πr2.
- Use a calculator for exact values when π is involved.
- Remember the relationship between diameter and radius: d = 2r.
- Practice converting between different units of measurement.
🔧 Note: It's helpful to use the diameter when the radius isn't provided directly; just divide it by 2 to find the radius.
In wrapping up this guide, it’s clear that understanding how to calculate the area of a circle not only equips you with a valuable mathematical skill but also builds a foundation for future studies in geometry and related fields. With the right approach, this topic becomes less intimidating and more manageable for students, enhancing their confidence in solving mathematical problems.
What if I only know the circumference of the circle?
+
If you know the circumference ©, you can find the radius using the formula (r = \frac{C}{2\pi}). Then use the area formula as usual.
How do I find the area when the radius is given in feet?
+
The process is identical; just ensure that your final answer is in square feet.
Can I use different approximations for π?
+
Yes, you can use different approximations like 3.14, 22⁄7, or even more precise values if needed.
