5 Essential Tips for Chords, Secants, Tangents Worksheet Solutions

Understanding chords, secants, and tangents is fundamental for students delving into the world of geometry. These geometric concepts are not only critical for academic success but also enrich one's grasp of spatial relationships. Whether you're a student grappling with these concepts for the first time or a teacher looking for effective ways to explain them, this guide provides detailed strategies and tips to master the chords, secants, and tangents worksheet solutions.
Identifying Key Geometric Properties

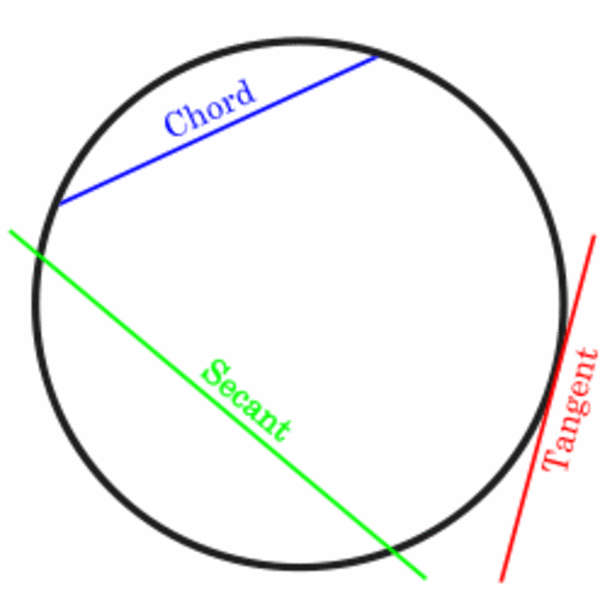
To effectively solve problems involving chords, secants, and tangents, it’s essential to first identify and understand their defining characteristics:
- Chords: A line segment with both endpoints on the circumference of the circle.
- Secants: A line that intersects the circle at two points.
- Tangents: A line that touches the circle at exactly one point, creating a right angle with the radius at the point of tangency.
Consider the following image to visualize these properties:

Tip 1: Use Definitions for Foundation

The definitions are more than just labels; they form the foundation for problem-solving:
- Know that the radius is perpendicular to the tangent at the point of tangency.
- Remember that a secant will intersect a tangent outside the circle at the square of the external segment equals the product of the secant and the whole external segment.
🔎 Note: Always start by drawing the circle and the chords, secants, or tangents to better visualize the problem.
Tip 2: Practice With Multiple Scenarios

Different problem sets can present various scenarios where:
- One chord intersects another chord inside the circle.
- A secant and a tangent intersect outside the circle.
- Secants intersect within or outside the circle.
Use these scenarios to:
- Practice calculating angles using the inscribed angle theorem or the tangent-secant theorem.
- Determine arc lengths or chord lengths based on given secant and tangent lengths.
Here’s how these scenarios might look in a table:
| Scenario | Problem Statement | Solution Method |
|---|---|---|
| Chord-Chord | Two intersecting chords | Use chord-chord power theorem |
| Secant-Tangent | External point, one secant, and one tangent | Apply the tangent-secant power theorem |
| Secant-Secant | Two secants intersecting outside the circle | Secant-secant power theorem |

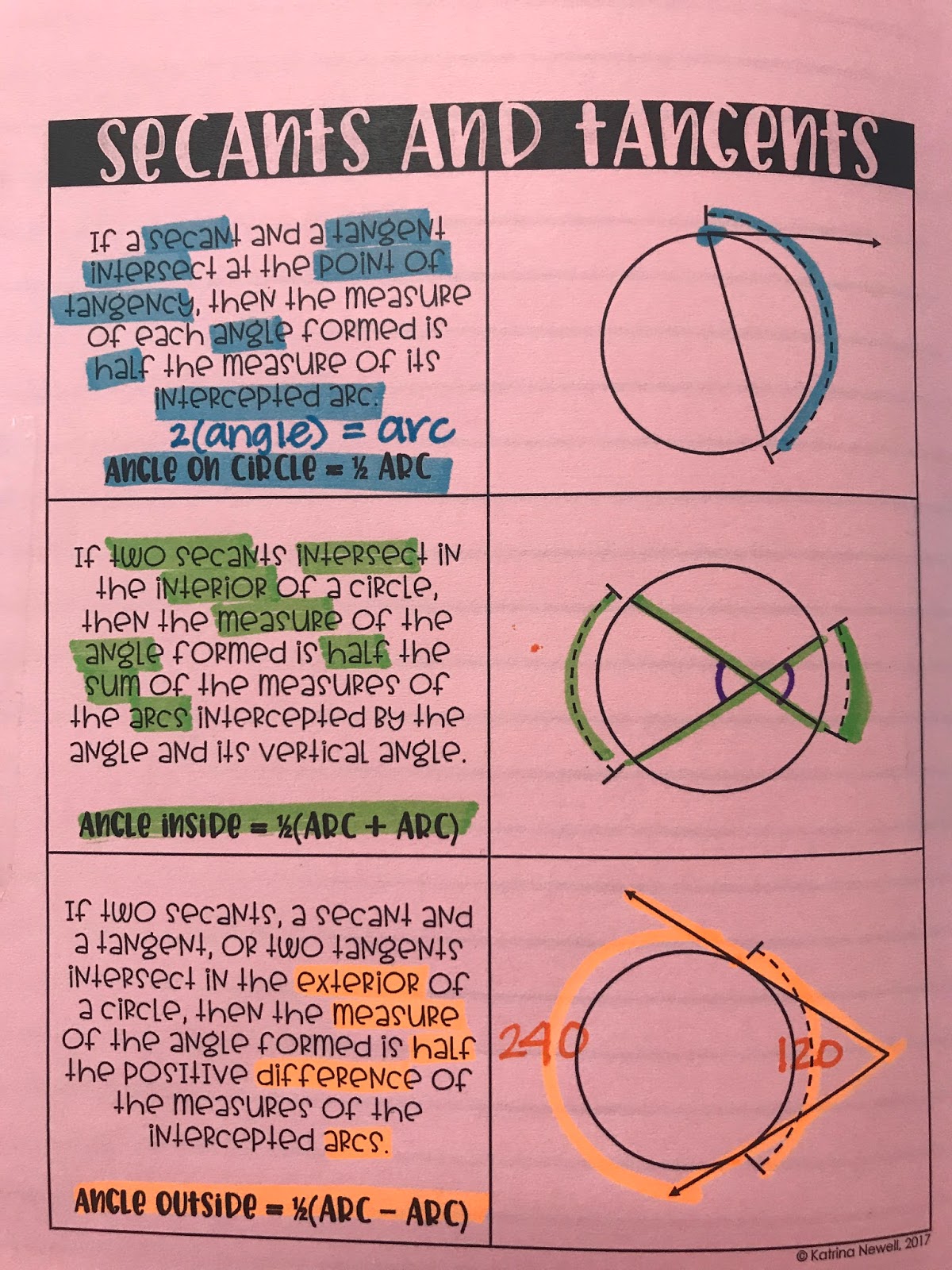
Tip 3: Apply Theorems Logically

Using the right theorem at the right time is key:
- Chord Theorem: When two chords intersect within a circle, the product of the segments of one chord equals the product of the segments of the other.
- Tangent-Secant Theorem: If a tangent and secant meet at an external point, the square of the tangent segment equals the product of the secant segment and its external segment.
These theorems help in finding lengths, angles, or even chord lengths within different problems.
Tip 4: Visualize Solutions
Visualization can greatly aid in solving problems:
- Sketch the circle and all given segments or angles.
- Identify if the problem requires direct application of theorems or if additional geometric constructions are needed.
- Use different colors or line styles to distinguish chords, secants, and tangents in your sketches.
🎨 Note: Visualization not only helps in solving the problem but also reinforces your understanding of the concepts.
Tip 5: Review Past Mistakes

Revisiting and analyzing past errors is a powerful learning tool:
- Identify common mistakes, like misinterpreting which theorem to apply.
- Look for patterns in errors related to angles or lengths.
- Revise the necessary theorems and properties to avoid repetition of the same errors.
In wrapping up, remember that mastering chords, secants, and tangents involves a combination of memorization, practice, and understanding. Start with the definitions, apply them in different scenarios, use appropriate theorems logically, and always visualize your solutions. Learning from past mistakes will guide you towards a deeper understanding, making complex geometry problems more manageable.
What is the difference between a chord and a secant?
+
A chord is a line segment with both endpoints on the circle, while a secant is a line that cuts through the circle at two points.
How do tangents and secants interact when they intersect outside a circle?

+
If a tangent and a secant intersect outside a circle, the square of the length of the tangent segment equals the product of the entire secant segment and its external part.
What are some common mistakes in chord, secant, and tangent problems?
+
Common mistakes include misapplying theorems, confusing which segment lengths to use, or overlooking geometric properties like the perpendicularity of a tangent to a radius at the point of tangency.
Related Terms:
- Tangents Worksheet answer Key



