5 Tips to Calculate Triangle Centroid Easily
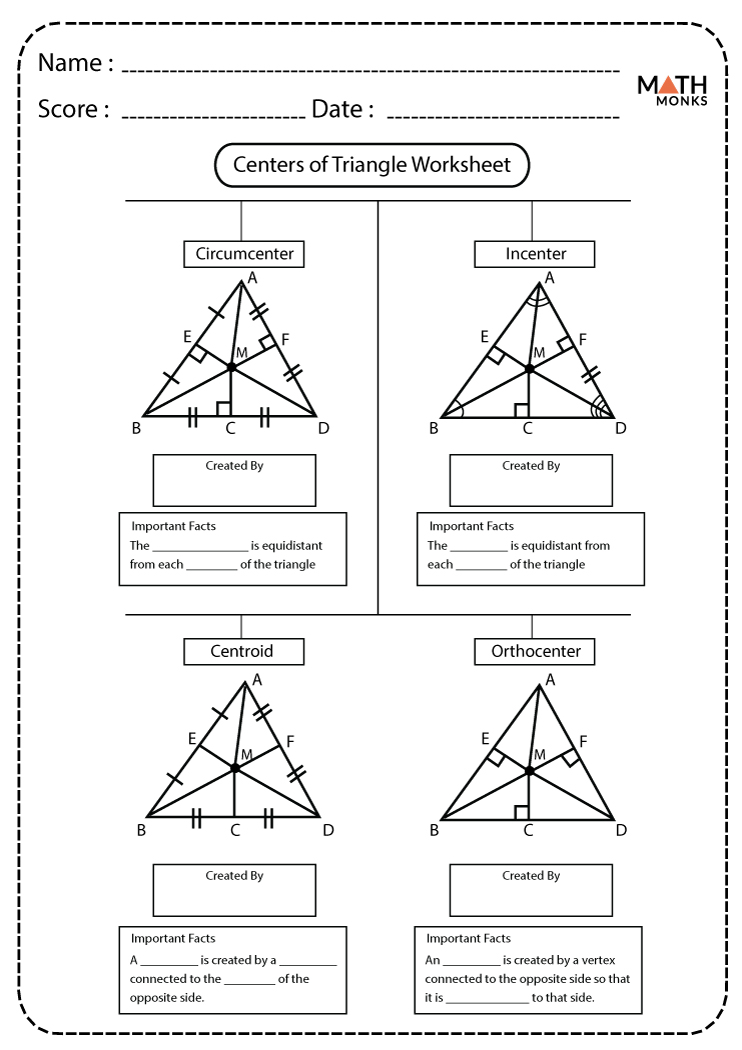
The centroid of a triangle is a crucial point of interest in geometry, representing the geometric center or the balance point where the triangle would balance if it were placed on a tip. This point is where the medians of the triangle intersect. A median is a line segment joining a vertex to the midpoint of the opposite side. Here are five tips to help you calculate the centroid easily:
1. Use the Formula for Coordinates

When dealing with a triangle in the coordinate plane, you can find the centroid using the formula:
Centroid (G) = ((\frac{x1 + x2 + x3}{3}, \frac{y1 + y2 + y3}{3}))
- Here, (x1, y1), (x2, y2), and (x3, y3) are the coordinates of the vertices of the triangle.
- This simple formula makes the calculation straightforward:
<p class="pro-note">🔖 Note: Ensure that you input the coordinates correctly to avoid calculation errors.</p>
2. Visualize the Triangle

Sketching the triangle on graph paper or using a coordinate geometry software can help visualize the medians and their intersection. This can:
- Reduce errors by confirming the geometric concept visually.
- Help understand how the centroid relates to other triangle properties like incenter and orthocenter.
3. Leverage Symmetry

Triangles often exhibit symmetry, which can simplify calculations:
- For an isosceles or equilateral triangle, draw a perpendicular from the base to the apex, and you’ll find that the centroid lies on this line of symmetry.
- This method leverages geometric properties to reduce the complexity of calculations:
<p class="pro-note">🌟 Note: Symmetry can often lead to simpler methods to calculate other geometric elements like circumcenter or orthocenter.</p>
4. Use Centroid Theorem

The Centroid Theorem states that each median of a triangle divides it into two segments such that the ratio of the longer segment to the entire median is 2:1:
- Knowing this ratio, you can calculate the position of the centroid along any median:
<p class="pro-note">📚 Note: This theorem applies universally to all triangles, whether scalene, isosceles, or equilateral.</p>
5. Apply Vector Calculus
For advanced users, vector calculus provides a powerful method for finding the centroid:
- Define vertices as vectors (\mathbf{a}, \mathbf{b},) and (\mathbf{c}).
- The centroid (\mathbf{G}) can be found using the vector equation:
- (\mathbf{G} = \frac{\mathbf{a} + \mathbf{b} + \mathbf{c}}{3})
This approach is particularly useful in 3D space or when dealing with complex coordinate systems: ```html
💡 Note: Vector methods can also be applied for finding centroids of polygons or polyhedrons.
```These tips provide an array of approaches tailored to different levels of understanding and complexity, ensuring that calculating the centroid of a triangle can be both accurate and insightful. Understanding these methods not only aids in geometry but also opens up applications in mechanics, physics, and engineering where the concept of balance is critical. By applying these tips, you can efficiently determine the centroid of any triangle, enhancing both your problem-solving skills and your appreciation of geometric principles.
What is the practical application of finding a triangle’s centroid?

+
The centroid is used in engineering to find the center of mass, in graphics to determine balance points for objects, and in mathematics to explore properties of triangles like stability and symmetry.
Can the centroid be outside of a triangle?

+
No, the centroid of a triangle is always located within the triangle, due to the property of medians intersecting at the centroid.
How does the centroid relate to other triangle centers?

+
The centroid, incenter (center of the incircle), circumcenter (center of the circumcircle), and orthocenter are all related by the Euler line. The centroid divides the Euler line in the ratio 2:1 between the orthocenter and circumcenter.
Why is knowing the centroid important in physics?

+
In physics, the centroid represents the point where the system’s mass or weight is considered to be concentrated, making it crucial for understanding the balance and stability of objects.
How does the centroid differ from the orthocenter?

+
The centroid is where the medians intersect, while the orthocenter is where the altitudes of the triangle meet. Unlike the centroid, the orthocenter can lie outside the triangle in an obtuse-angled triangle.



