Master Central Angles with Our Engaging Worksheet

Understanding Central Angles

Central angles are a fundamental concept in geometry, playing a crucial role in understanding circles and their properties. A central angle is an angle formed by two radii of a circle that have a common endpoint, which is the center of the circle. The measure of the central angle is equivalent to the arc it intercepts.
Importance of Central Angles

Understanding central angles has several practical applications in mathematics:
- Calculating the circumference or area of a circle.
- Solving for arc lengths or areas of sectors.
- Helping in various real-world applications like mechanical design, physics, and engineering.
🔖 Note: A central angle whose measure is 180° divides the circle into two equal halves, forming a semicircle.
Worksheet Overview
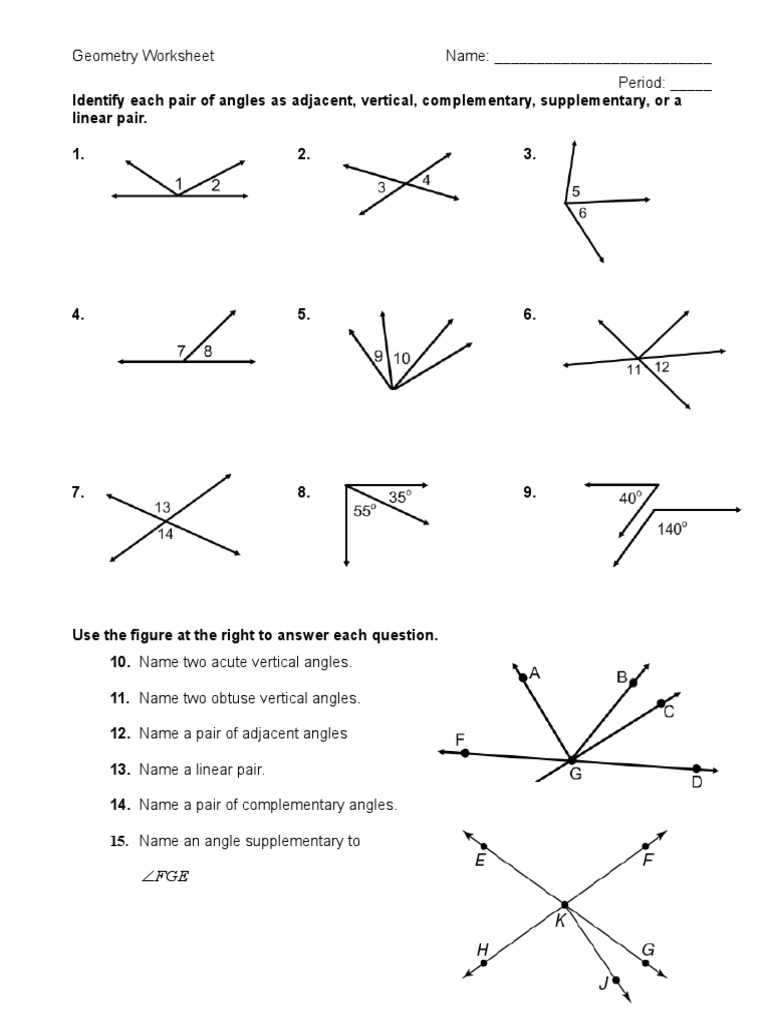
Our worksheet on central angles is designed to reinforce your understanding through a series of interactive exercises:
- Identifying central angles in various circle configurations.
- Measuring central angles with a protractor.
- Calculating arc lengths and sector areas based on central angles.
Exercise 1: Identifying Central Angles

In this exercise, students are asked to:
- Identify and name the central angles in given diagrams.
- Determine whether each angle is acute, right, obtuse, or reflex.
🔍 Note: Reflex angles are greater than 180° but less than 360°.
Exercise 2: Measuring Central Angles

The second part of the worksheet focuses on:
- Using a protractor to measure central angles accurately.
- Drawing and labeling central angles with specific measures.
📐 Note: Make sure your protractor is properly aligned with one of the radii when measuring angles.
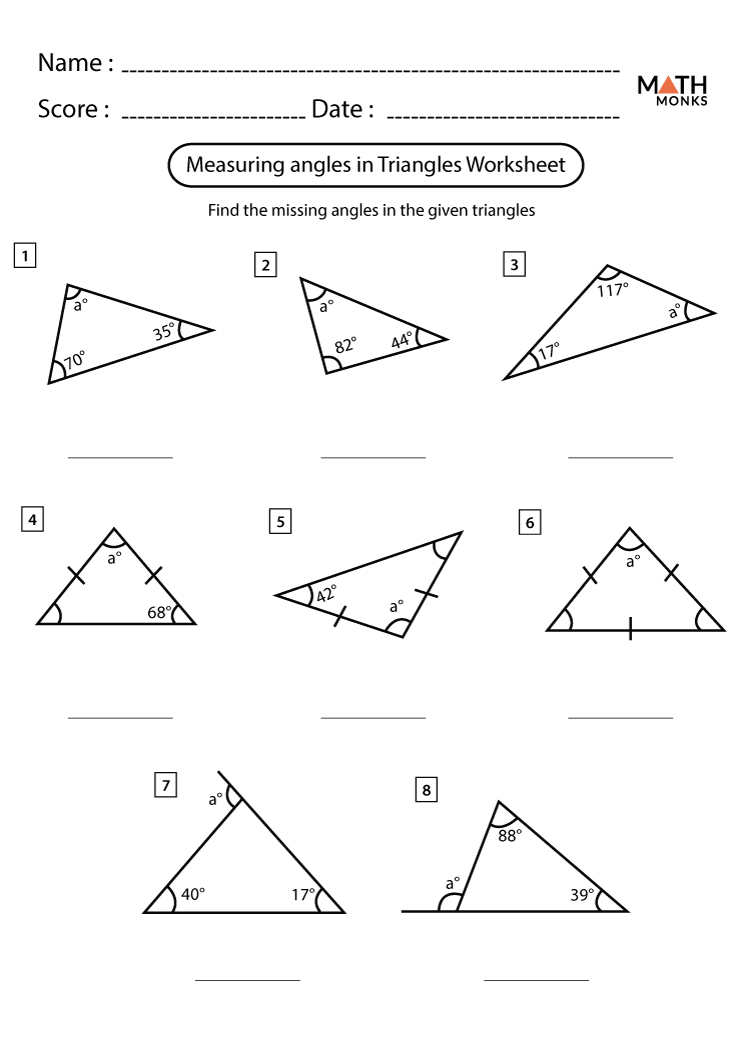
Exercise 3: Calculation Exercises

This section tests students' ability to:
- Calculate the arc length given the radius and central angle.
- Find the area of sectors when central angles and radii are known.
How to Use the Worksheet

- Preparation: Ensure you have a protractor, ruler, pencil, and the worksheet.
- Study Examples: Review the examples provided for each exercise type to understand the approach.
- Do the Exercises: Work through each problem systematically, checking your answers with the provided solutions or keys.
- Ask for Help: If you're stuck, don't hesitate to ask for clarification from your teacher or peers.
Benefits of Practicing with This Worksheet

Engaging with this worksheet will help students:
- Develop visual intuition about angles within circles.
- Improve precision in measurements.
- Gain confidence in applying geometric principles.
- Prepare for exams or assessments on geometry.
📚 Note: Regular practice using such worksheets can significantly enhance your understanding and retention of geometric concepts.
Final Thoughts
By working through the various exercises in our central angles worksheet, you not only bolster your grasp of this essential geometric concept but also sharpen your problem-solving skills. Engaging with these problems in a structured manner helps in not just memorizing facts, but truly understanding the relationships between angles, radii, and arcs in circles. This practical application ensures a thorough understanding, making geometry both fun and intellectually rewarding.
What makes an angle a central angle?

+
A central angle is formed by two radii of a circle sharing a common endpoint at the circle’s center. The measure of this angle is the same as the arc it intercepts.
Can a central angle be greater than 180°?

+
Yes, central angles can be up to 360°, making them reflex angles when greater than 180°.
How does the central angle relate to the circle’s circumference?

+
The arc length intercepted by a central angle is proportional to the circumference of the circle; specifically, the arc length is (angle/360) * circumference.