5 Key Insights: Central and Inscribed Angles Worksheet Answers

Understanding Central and Inscribed Angles: A Deep Dive into Key Insights

Geometry, as a branch of mathematics, offers a variety of concepts and principles that are not only fascinating but also immensely useful in understanding spatial relationships. Among these, central angles and inscribed angles stand out due to their fundamental roles in circle geometry. In this blog post, we will explore five key insights into these angles, helping you grasp their properties and applications with clarity and precision.
Key Insight #1: Definition and Relation

A central angle is an angle whose vertex lies at the center of a circle, and its sides are two radii of the circle. Conversely, an inscribed angle has its vertex on the circle and its sides passing through the endpoints of an arc.
🌟 Note: The measure of an inscribed angle is half that of a central angle intercepting the same arc.
- Central Angle: The angle formed by two radii that meet at the center of the circle.
- Inscribed Angle: The angle formed by two chords that meet on the circumference of the circle.
Key Insight #2: Angle Measurement Formulas

The relationship between central and inscribed angles can be summarized with the following formulas:
- Central Angle: \text{Central Angle} = 2 \times \text{Inscribed Angle}
- Inscribed Angle: \text{Inscribed Angle} = \frac{1}{2} \times \text{Central Angle}
💡 Note: These formulas hold true when the arcs intercepted by these angles are the same.
Key Insight #3: Types of Arcs and their Angles

There are two types of arcs on a circle: minor arc and major arc. Here’s how they relate to central and inscribed angles:
| Type of Arc | Relation to Angle |
|---|---|
| Minor Arc | Its length is less than half the circumference, associated with the central angle less than 180 degrees. |
| Major Arc | Its length is more than half the circumference, associated with a central angle greater than 180 degrees. |
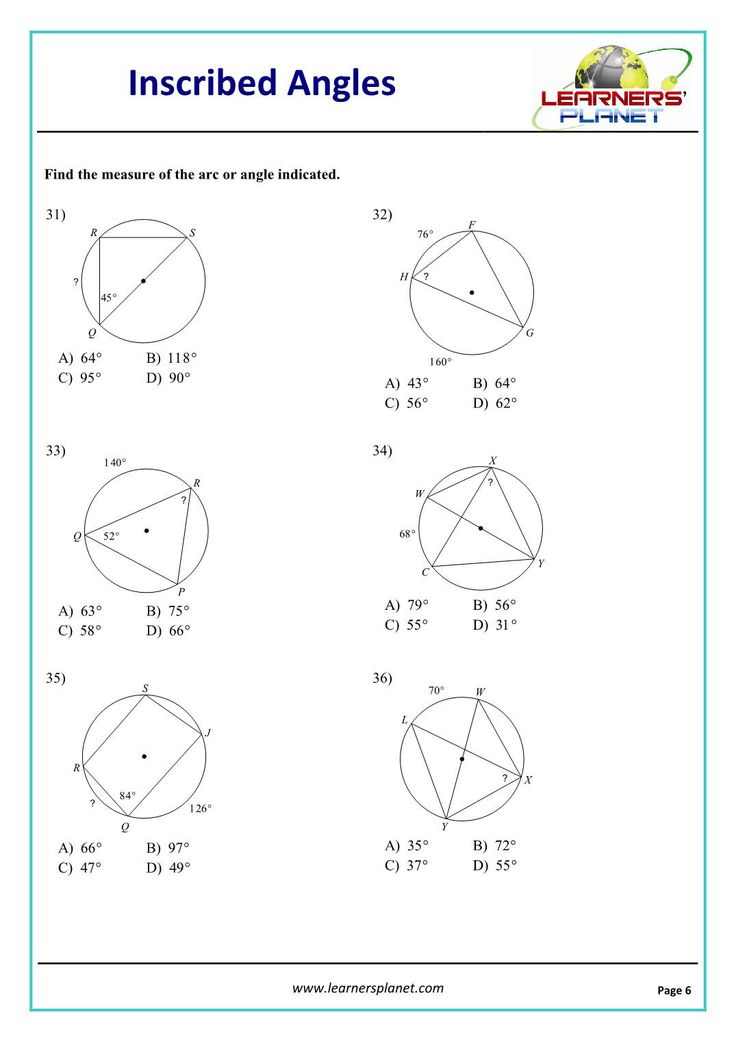
Key Insight #4: Properties of Inscribed Angles
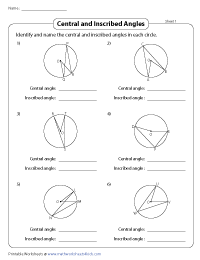
Inscribed angles have some unique properties that are important for understanding circle geometry:
- Inscribed Angle Theorem: An inscribed angle that subtends the same arc will always have the same measure.
- Opposite Angles: Opposite angles in an inscribed quadrilateral are supplementary, meaning they add up to 180 degrees.
- Tangent-Secant Angles: The angle formed by a tangent and a secant line at the point of tangency is half the angle formed by the secant and the chord that creates the same arc.
📍 Note: The angle between a tangent and a chord through the point of tangency equals the inscribed angle on the opposite side of the same arc.
Key Insight #5: Practical Applications

Understanding central and inscribed angles goes beyond theoretical geometry; it has practical implications in various fields:
- Architecture: Determining the arc of a building's curve or dome.
- Navigation: Calculating bearings and headings with angle subtended by a known arc.
- Computer Graphics: Rendering circles and curves in 2D or 3D space, where these angles help in defining curves and ellipses.
In wrapping up, central and inscribed angles are not just foundational to circle geometry; they are instrumental in understanding many spatial relationships in our world. By exploring these key insights, we’ve covered definitions, formulas, properties, and practical applications, allowing us to appreciate the depth and utility of these geometric concepts.
What’s the difference between a central angle and an inscribed angle?
+
A central angle has its vertex at the center of the circle, with its sides being radii, while an inscribed angle has its vertex on the circumference, with its sides being chords or secants.
Can an inscribed angle ever be larger than the central angle?
+
No, by the definition and formula provided, an inscribed angle is always half the measure of the central angle that intercepts the same arc.
How does knowing these angles help in real-world scenarios?

+
They help in architecture for designing curved structures, in navigation for calculating distances and bearings, and in computer graphics for rendering accurate shapes and curves.