Central Angles and Arcs Worksheet Answer Key Revealed

In the fascinating realm of geometry, understanding angles and their relationships with arcs plays a crucial role. Central angles and arcs are fundamental concepts that help us analyze and measure circular parts of objects, from the intricacies of machinery to the aesthetics of architecture. This blog post aims to unveil the Central Angles and Arcs Worksheet Answer Key, providing insight into how these concepts are interwoven to create a clearer picture of geometric understanding.
Understanding Central Angles

A central angle is defined as the angle whose vertex is the center of a circle, and its sides intersect the circle at two distinct points. The size of a central angle determines the length of the arc it intercepts and the area of the sector it forms:
- Degree Measure: A central angle can be measured in degrees, where 360 degrees make up a full circle.
- Radian Measure: Alternatively, radians are used for measurement. Here, one full circle equals 2π radians.
Here are key points to remember about central angles:
- If the central angle is 90 degrees, it is known as a right angle, forming a quarter of a circle.
- A central angle of 180 degrees is known as a straight angle, creating a semicircle or half of a circle.
- Angles less than 180 degrees but greater than 0 degrees are known as acute or obtuse angles depending on whether they are less than or greater than 90 degrees.

📏 Note: Radian measure offers a natural unit for angle measurement because it relates directly to the length of the arc that the angle subtends.
The Concept of Arcs

An arc is a part of the circumference of a circle, and its length depends on the central angle subtended by it. Here’s what you need to know:
- The length of an arc is proportional to the central angle and the radius of the circle.
- When an arc is a segment of a circle where the central angle is less than 180 degrees, it is known as a minor arc.
- Conversely, when the central angle exceeds 180 degrees, we have a major arc.
Here's an illustrative example:
| Central Angle | Arc Length |
|---|---|
| 60 degrees | π/3 * r (where r is the radius) |
| 90 degrees | π/2 * r |
| 180 degrees | π * r |

📝 Note: The formula to calculate the length of an arc is (θ/360°) * 2πr, where θ is the measure of the central angle in degrees and r is the radius of the circle.
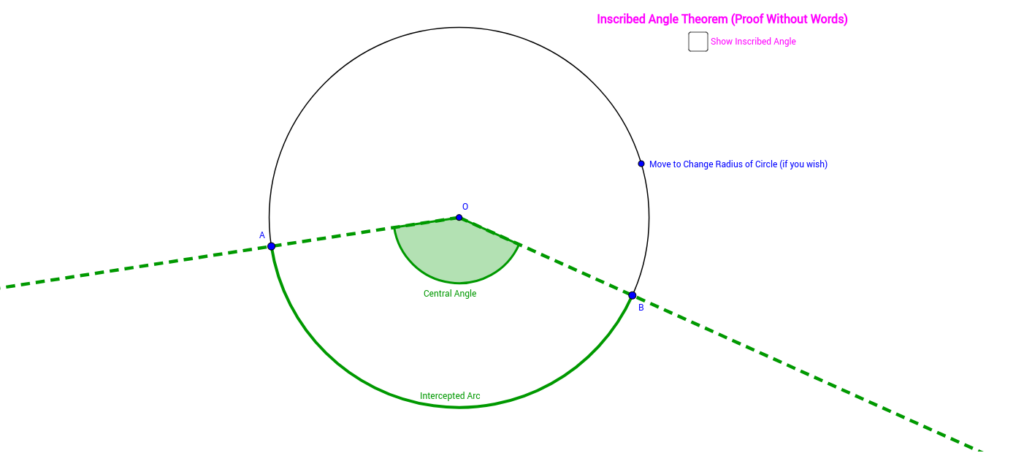
Relating Central Angles to Inscribed Angles

The relationship between central angles and inscribed angles, where the vertex lies on the circumference of the circle, is a fascinating aspect:
- An inscribed angle measures half the central angle that intercepts the same arc.
- This relation is extremely useful for solving problems and calculating arc lengths without always having to measure the central angle directly.
Central Angles and Arcs Worksheet Answer Key
Let’s delve into the worksheet and reveal the answers:
- Question 1: Find the length of the arc intercepted by a central angle of 72 degrees in a circle with a radius of 5 cm.
- Question 2: If the measure of the central angle is 250 degrees, what type of arc does it form?
- Question 3: Determine the area of the sector defined by a central angle of 45 degrees in a circle with a diameter of 10 cm.
Answer: Using the formula mentioned earlier, the arc length = (72⁄360) * 2π * 5 = 2π/5 * 5 = 2π cm ≈ 6.28 cm.
Answer: This central angle subtends a major arc.
Answer: The radius r = 5 cm, and the sector area = (θ/360) * πr² = (45⁄360) * π * 5² = (1⁄8) * π * 25 = 25π/8 cm² ≈ 9.82 cm².
The detailed understanding of central angles and arcs allows students to solve such problems confidently. As we've explored, central angles provide the pivot point around which arcs are calculated and sectors are formed, enhancing the geometrical analysis of circular properties.
In wrapping up, the essence of central angles and their relation to arcs goes beyond the numbers and formulas. They teach us about the inherent beauty in the symmetry and unity of a circle, the simplest yet most profound shape in geometry. The precise relationship between angles and arcs, both in terms of measurement and conceptual understanding, forms the backbone of many advanced geometric and trigonometric applications, from engineering designs to everyday applications in the field.
What are the different types of arcs?

+
There are primarily two types of arcs based on the central angle they subtend: minor arc (less than 180 degrees) and major arc (more than 180 degrees but less than 360 degrees).
Why are inscribed angles always half the measure of central angles?

+
This relationship stems from the circle’s symmetry. The measure of an inscribed angle is half the measure of the central angle that intercepts the same arc because the circle can be divided into two equal halves by the diameter, leading to this consistent ratio.
How can understanding central angles and arcs be useful in real life?

+
Central angles and arcs play crucial roles in fields like architecture, engineering, astronomy, and even art, where symmetry and proportions are key. For instance, understanding the distribution of light around a light source or calculating the exact curvature of roads or tracks can be simplified with this knowledge.



