Central Angles And Arc Measures Worksheet

Understanding Central Angles and Arc Measures

When dealing with circles, it’s essential to comprehend the relationship between central angles and arc measures. This concept is crucial in geometry and trigonometry, and it has numerous practical applications. In this article, we’ll delve into the world of central angles and arc measures, exploring their definitions, properties, and uses.
What are Central Angles?

A central angle is an angle whose vertex is at the center of a circle, and its sides pass through the endpoints of an arc. The measure of a central angle is equal to the measure of its intercepted arc. Central angles can be acute, right, or obtuse, depending on the measure of the arc they intercept.
What are Arc Measures?
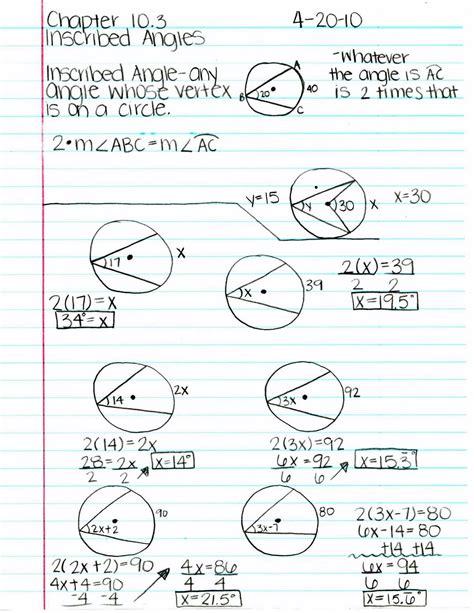
An arc measure is the measure of the arc intercepted by a central angle. Arc measures can be expressed in degrees or radians. When a central angle measures θ degrees, its intercepted arc measures θ degrees as well. Arc measures are used to calculate the length of an arc, the circumference of a circle, and the area of a sector.
Relationship Between Central Angles and Arc Measures

The relationship between central angles and arc measures is straightforward: the measure of a central angle is equal to the measure of its intercepted arc. This means that if a central angle measures 60 degrees, its intercepted arc also measures 60 degrees.
| Central Angle Measure | Arc Measure |
|---|---|
| 30° | 30° |
| 90° | 90° |
| 180° | 180° |

Properties of Central Angles and Arc Measures

Here are some essential properties of central angles and arc measures:
- The sum of the measures of two central angles that intercept the same arc is equal to the measure of the arc.
- If two arcs are congruent, their corresponding central angles are congruent.
- If two central angles are congruent, their corresponding arcs are congruent.
📝 Note: When solving problems involving central angles and arc measures, it's essential to consider the properties listed above.
Real-World Applications of Central Angles and Arc Measures

Central angles and arc measures have numerous practical applications in various fields, including:
- Architecture: When designing circular structures, architects need to calculate the measure of central angles and arc measures to ensure stability and symmetry.
- Engineering: Central angles and arc measures are used in the design of circular motion systems, such as gears and pulleys.
- Navigation: Understanding central angles and arc measures is crucial for navigation, as it helps calculate distances and directions between locations.
Worksheet: Central Angles and Arc Measures
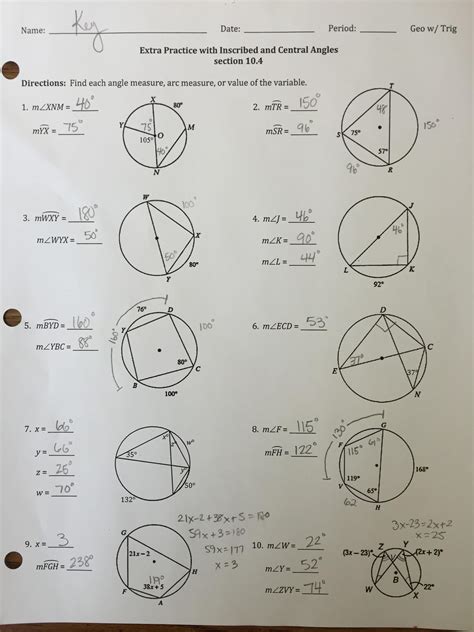
Now that we’ve covered the basics of central angles and arc measures, it’s time to practice with a worksheet. Here are five problems to help you reinforce your understanding:
- If a central angle measures 45°, what is the measure of its intercepted arc?
- If an arc measures 120°, what is the measure of its central angle?
- In a circle, two central angles intercept the same arc. If one angle measures 30°, what is the measure of the other angle?
- If two arcs are congruent, what can be concluded about their corresponding central angles?
- In a circular motion system, a gear has a central angle of 90°. What is the measure of the arc intercepted by this angle?
📝 Note: Take your time to solve each problem, and make sure to apply the properties and concepts discussed in this article.
What is the relationship between central angles and arc measures?

+
The measure of a central angle is equal to the measure of its intercepted arc.
What are some real-world applications of central angles and arc measures?

+
Central angles and arc measures have applications in architecture, engineering, navigation, and more.
How do I solve problems involving central angles and arc measures?

+
Use the properties listed in this article, such as the sum of central angle measures equaling the arc measure, and apply them to the problem.
In conclusion, understanding central angles and arc measures is vital for success in geometry and trigonometry. By mastering these concepts, you’ll be able to tackle complex problems and apply your knowledge to real-world situations.
Related Terms:
- central angles worksheet pdf
- inscribed angle theorem worksheet pdf
- central and inscribed angles practice
- arcs and angles worksheet pdf
- worksheet inscribed angles and arcs
- central and inscribed angles pdf