5 Key Tips for Solving Angle Problems in Geometry
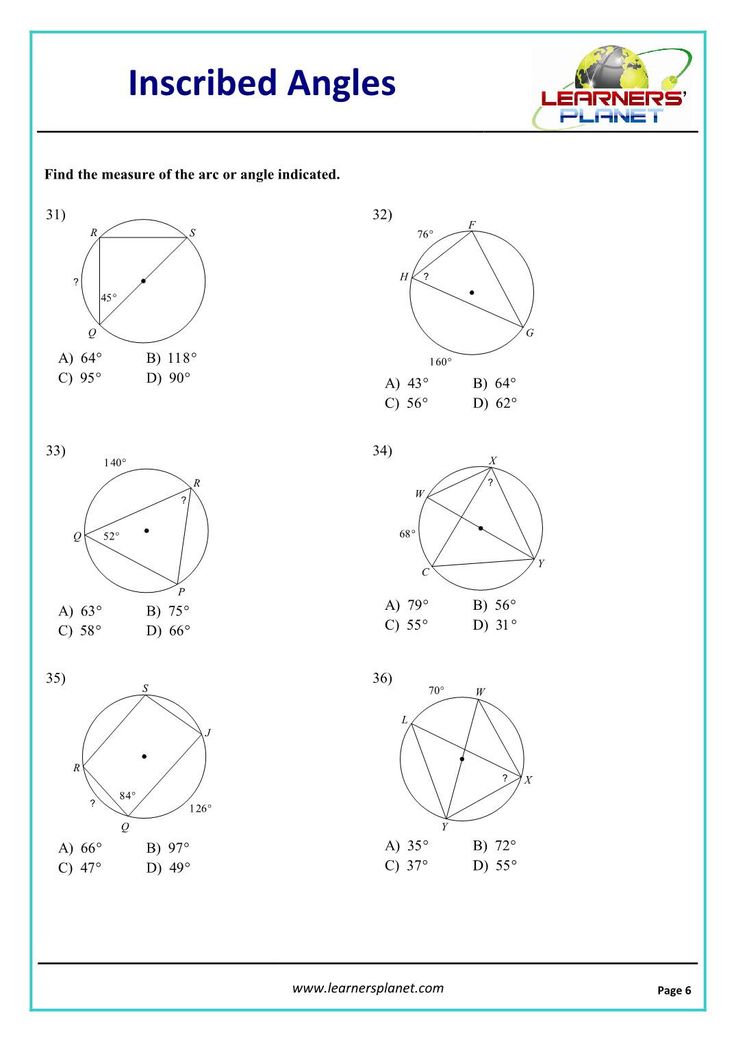
Are you struggling with solving angle problems in geometry? Whether you're a high school student or someone just looking to brush up on their geometry skills, mastering the art of solving angle problems is crucial for success in mathematics. Here, we'll explore five key strategies to help you tackle these problems with confidence.
Understanding Fundamental Angle Properties
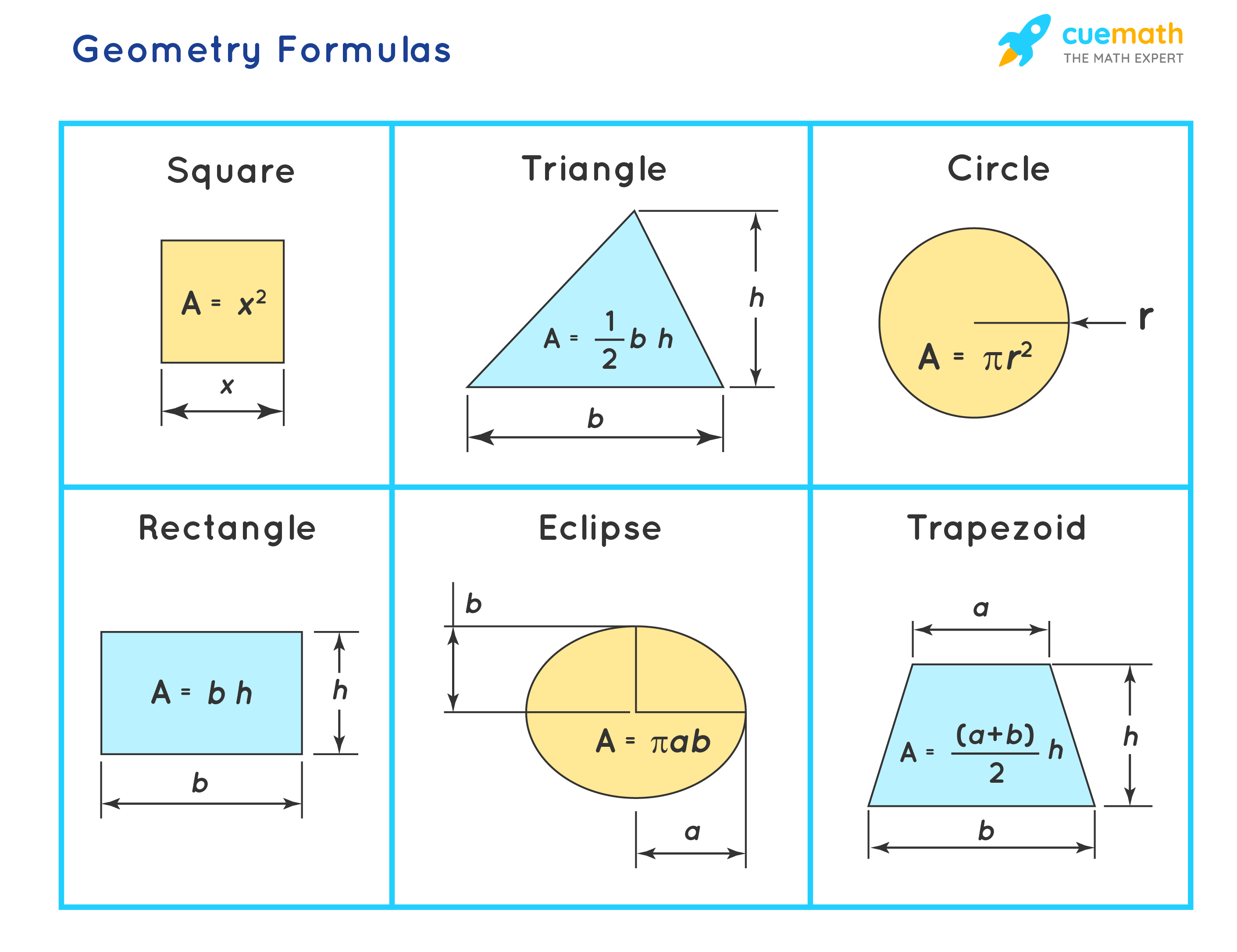
Before diving into complex problems, it’s essential to understand the basic properties of angles:
- Types of angles: Acute, obtuse, right, straight, and reflex angles.
- Sum of angles in a triangle: The total is always 180 degrees.
- Vertical angles: These are equal when two lines intersect.
- Adjacent angles: These share a common vertex and side but no interior points.
- Complementary and supplementary angles: Angles that add up to 90° and 180°, respectively.
Mastery of these properties will provide a solid foundation for solving more intricate angle problems.
Use Geometry Theorems and Postulates

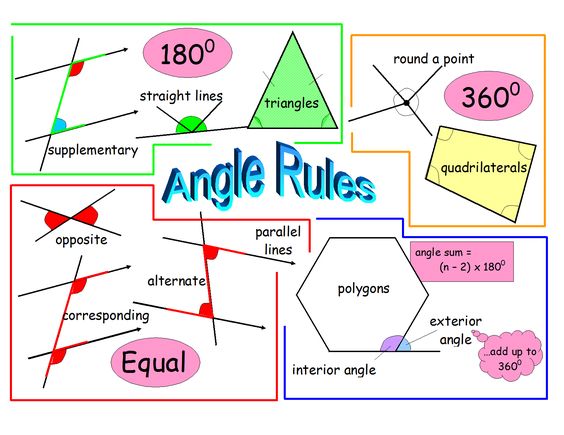
Geometry is built on theorems and postulates that help us understand angle relationships:
- The Angle Sum Theorem: The sum of the interior angles of a polygon can be calculated with (n - 2) × 180° where n is the number of sides.
- The Exterior Angle Theorem: An exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles.
- The Alternate Interior Angle Theorem: When a transversal cuts through two parallel lines, the alternate interior angles are congruent.
By applying these theorems, you can simplify problems that might initially seem unsolvable.
Practice with Real-World Scenarios
To make learning more engaging, relate angles to everyday scenarios:
- Architecture: Angles in buildings, bridges, and houses.
- Navigation: Angles used in finding directions or determining distances.
- Sports: Angles in snooker, billiards, or even golf shots.
💡 Note: Use your imagination to create or find scenarios that illustrate these angle problems.
Creating Visual Diagrams

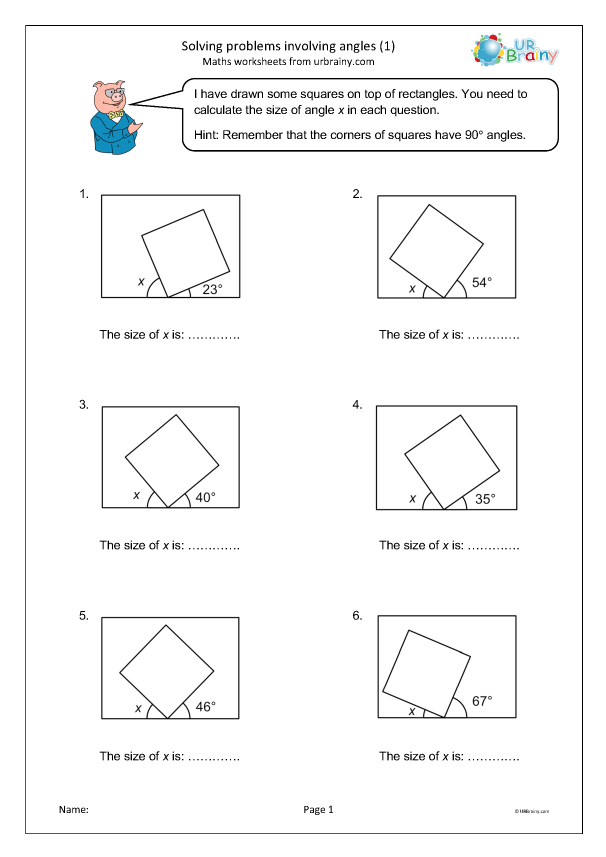
Always draw diagrams when working on geometry problems:
- Accurately sketch all known angles and lines.
- Label each part of the diagram with corresponding variables or values.
- Mark angles you need to find with question marks or letters.
This visual representation helps to conceptualize the problem and identify applicable geometric principles.
| Step | Description |
|---|---|
| 1 | Draw the geometric figure |
| 2 | Label all known angles and sides |
| 3 | Identify and mark unknown angles |
| 4 | Apply relevant theorems to find angles |

🚧 Note: Practice sketching as you solve; this builds muscle memory and improves spatial awareness.
Working Backwards from Given Angles
When direct solution paths are elusive, working backwards can be effective:
- Start with the angle you need to find.
- Identify what other angles must be known to find it.
- Work backward step-by-step until you reach known values or initial given information.
Here’s an example:
- If you know that ∠A + ∠B + ∠C = 180°, and ∠A is given, you can determine ∠B or ∠C by working backwards from the sum.
As we wrap up this exploration into mastering angle problems, remember that persistence and practice are key. These strategies not only help in solving individual problems but also in understanding the underlying geometry that governs them. Each problem is an opportunity to apply and reinforce your understanding of geometric principles.
What are vertical angles and why are they important?
+
Vertical angles are formed when two lines intersect, creating pairs of opposite angles. They are important because they are always congruent, providing a quick method to solve for unknown angles.
How can geometry problems be applied to real life?

+
Geometry has numerous real-life applications in fields like architecture, navigation, computer graphics, robotics, and even in daily activities like measuring distances or designing spaces.
What is the importance of sketching in geometry?

+
Sketching helps in visualizing complex geometric problems, allowing you to identify relationships between angles and sides, which is crucial for solving problems accurately.