Boyle's Law Worksheet Answers: Quick Guide for Students

Understanding Boyle's Law is fundamental for students studying chemistry, particularly in the fields of gas laws and thermodynamics. This law, named after the Irish scientist Robert Boyle, describes the inversely proportional relationship between the pressure and volume of a gas, when temperature and the amount of gas remain constant. This guide provides detailed answers to common Boyle's Law worksheet problems, helping students to solidify their understanding of this principle.
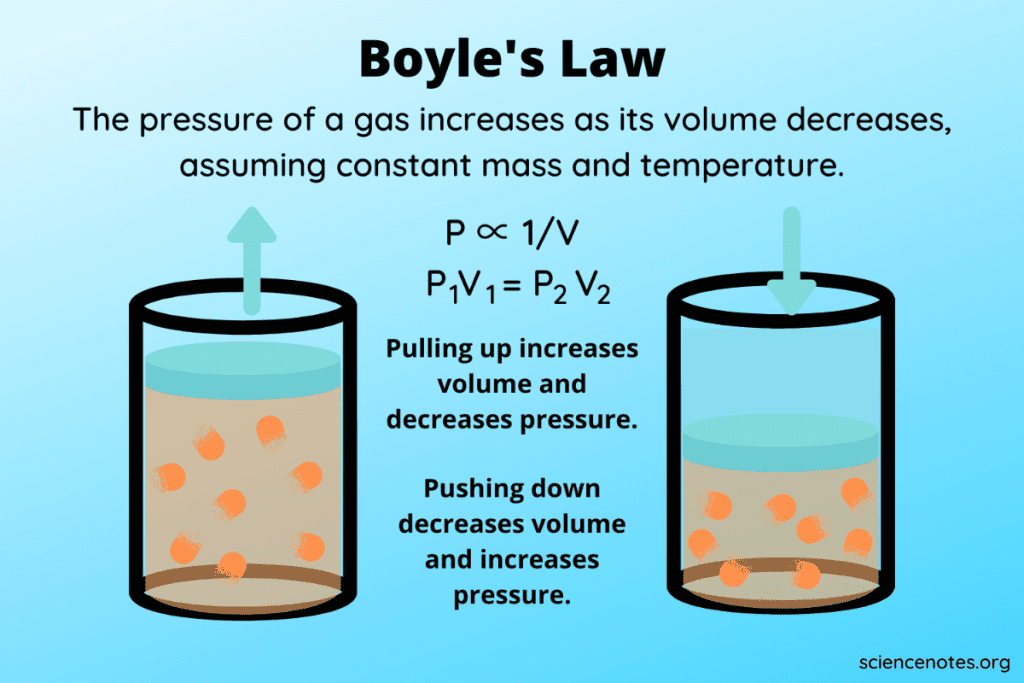
What is Boyle's Law?


Boyle's Law states that for a given mass of gas at constant temperature, the product of the pressure and volume is a constant:
\[P_1V_1 = P_2V_2\]
Boyle's Law Calculations

Example Problem 1: Basic Pressure-Volume Change

A container of gas has a volume of 2 liters at a pressure of 3 atmospheres. If the volume is reduced to 1 liter, what will be the new pressure?
- Initial Volume (V1) = 2 L
- Initial Pressure (P1) = 3 atm
- New Volume (V2) = 1 L
Using Boyle's Law:
\[P_1V_1 = P_2V_2\]
\[(3 \text{ atm}) (2 \text{ L}) = P_2 (1 \text{ L})\]
\[6 \text{ atm} \cdot \text{L} = P_2 (1 \text{ L})\]
\[P_2 = 6 \text{ atm}\]
🌡️ Note: Remember, the temperature is constant in this problem, which is a critical assumption for Boyle's Law to apply.
Example Problem 2: Changing Volume with Pressure

A gas with a pressure of 4 atm has a volume of 5 L. If you increase the pressure to 10 atm, what will be the new volume?
- Initial Pressure (P1) = 4 atm
- Initial Volume (V1) = 5 L
- New Pressure (P2) = 10 atm
Applying Boyle's Law:
\[4 \text{ atm} \cdot 5 \text{ L} = 10 \text{ atm} \cdot V_2\]
\[20 \text{ atm} \cdot \text{L} = 10 \text{ atm} \cdot V_2\]
\[V_2 = \frac{20}{10} \text{ L} = 2 \text{ L}\]
📌 Note: When pressure increases, the volume decreases proportionally, ensuring the product of pressure and volume remains constant.
Example Problem 3: Complex Scenario

Consider a gas at 600 mmHg with a volume of 300 cm³. If the volume is decreased to 150 cm³, what is the new pressure in mmHg?
- Initial Pressure (P1) = 600 mmHg
- Initial Volume (V1) = 300 cm³
- New Volume (V2) = 150 cm³
Using Boyle's Law:
\[(600 \text{ mmHg}) (300 \text{ cm}^3) = P_2 (150 \text{ cm}^3)\]
\[180000 \text{ mmHg} \cdot \text{cm}^3 = P_2 (150 \text{ cm}^3)\]
\[P_2 = \frac{180000}{150} \text{ mmHg} = 1200 \text{ mmHg}\]
Understanding the Implications

Boyle’s Law not only helps students solve numerical problems but also provides insights into real-world applications:
- Scuba Diving: Divers need to understand how pressure changes affect the volume of air in their lungs and equipment.
- Medical Use: In medical settings like spirometry, Boyle’s Law is used to measure lung capacity and function.
- Industrial Applications: Compressing gases in industrial processes or storage.
In this exploration of Boyle's Law, we've covered:
- The principle behind Boyle's Law.
- Solving typical Boyle's Law problems.
- Practical applications where this law is relevant.
Remember, mastering Boyle's Law involves more than just the calculations; it's about understanding the behavior of gases under changing conditions. This understanding extends beyond academic exercises into practical applications in various fields, making it a cornerstone in the study of physical sciences.
Why is Boyle’s Law important in medical fields?

+
In medicine, Boyle’s Law is crucial for diagnosing respiratory issues through spirometry, where the volume and pressure of air exhaled by a patient is measured to assess lung function.
Can Boyle’s Law be applied to liquids?
+
Boyle’s Law applies specifically to gases. Liquids have much less compressibility due to their molecular structure, making the law less relevant for liquid behavior.
How does temperature affect Boyle’s Law?

+
Boyle’s Law assumes constant temperature. Changes in temperature would affect the behavior of gas, introducing variables like Charles’s Law into the equation.