Box and Whiskers Plot Mastery: Learn Effectively

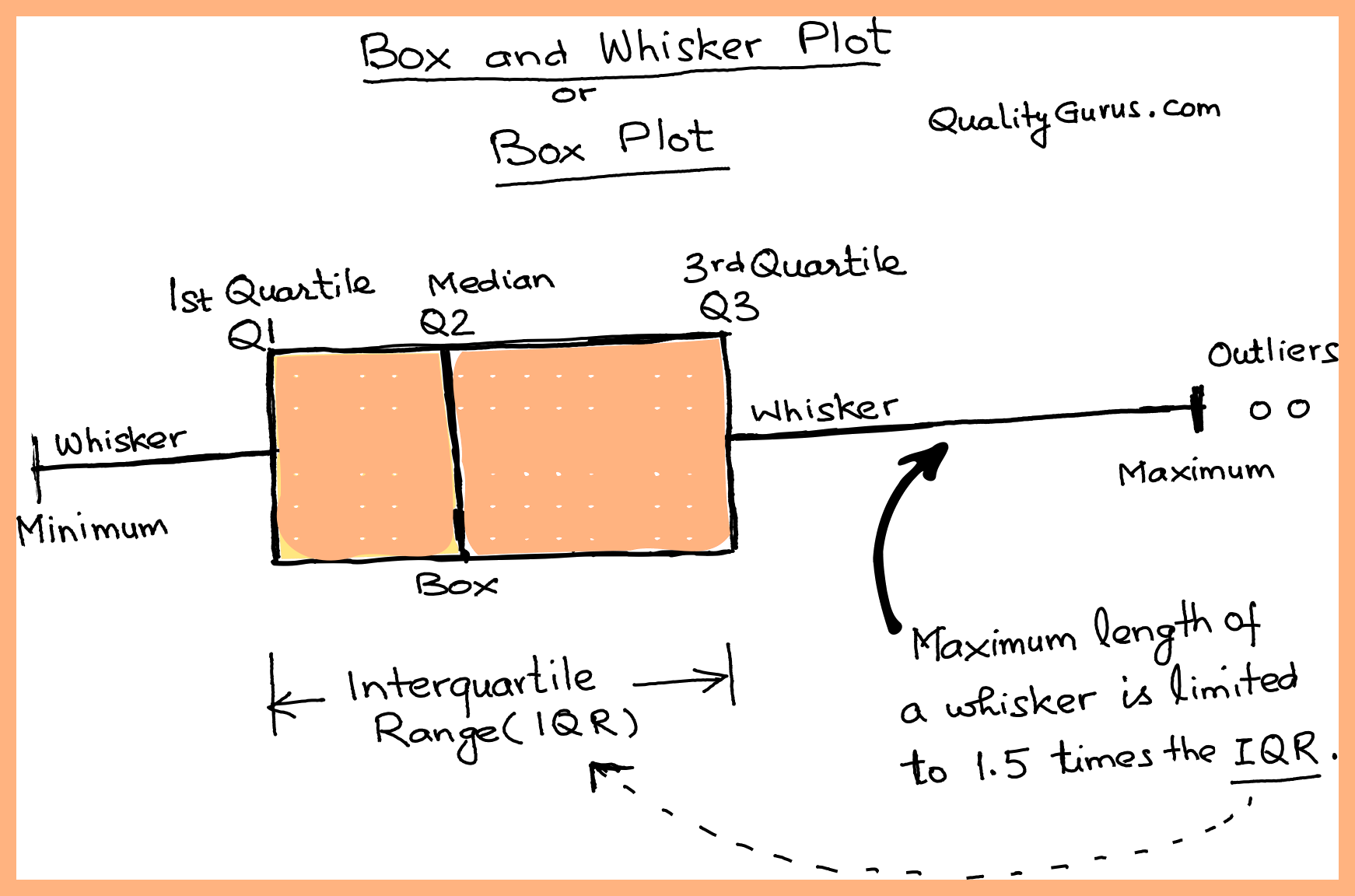
The box and whiskers plot, commonly known as a box plot, is an essential tool in the field of statistics for visualizing the distribution of data through its five-number summary: minimum, first quartile (Q1), median (Q2), third quartile (Q3), and maximum. This graphical representation not only displays the spread and skewness but also helps in identifying outliers in a dataset. In this article, we will delve into how to master box plots, understand their creation, interpretation, and application in various contexts.
Understanding Box and Whiskers Plots

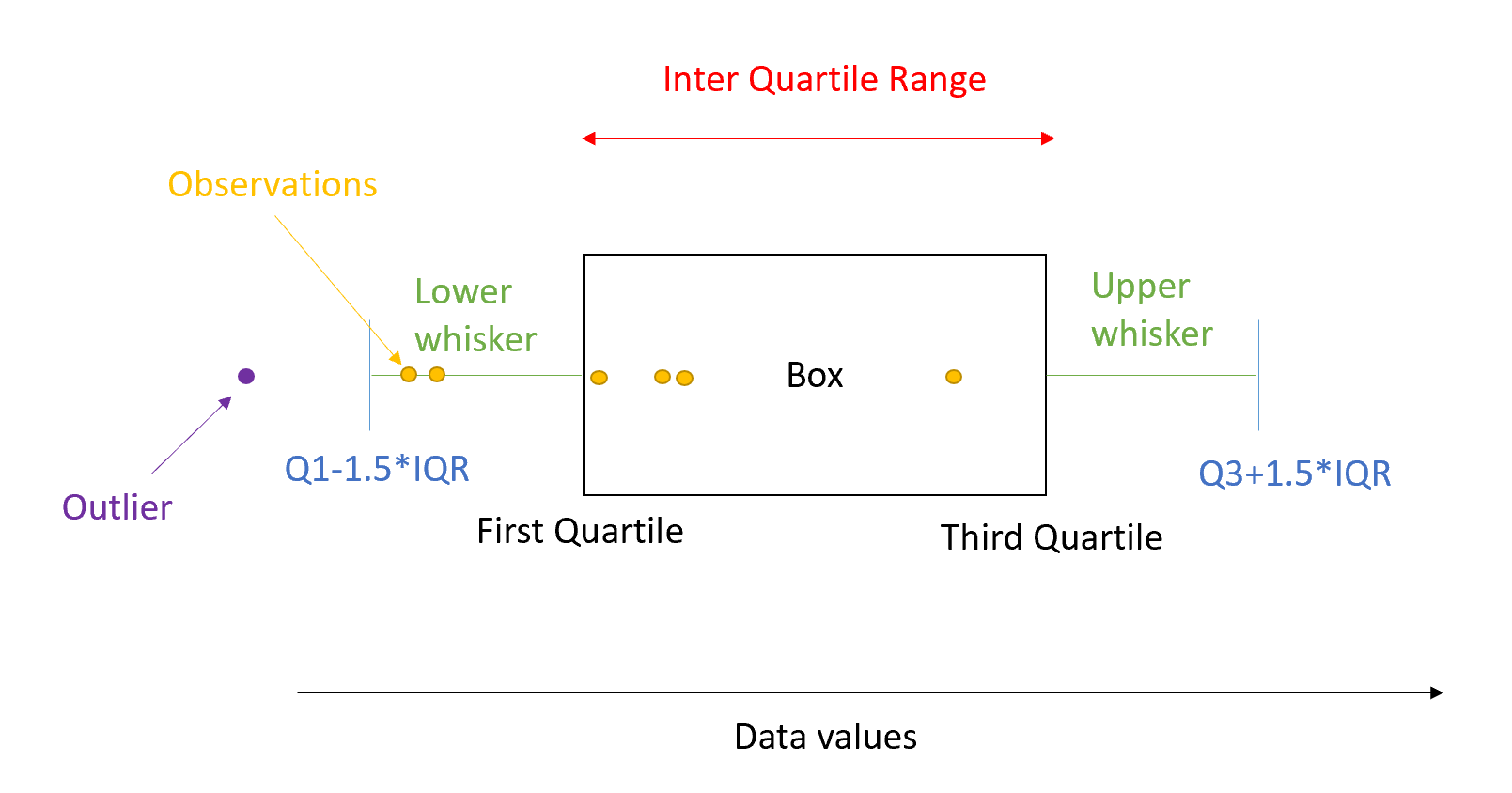
A box plot encapsulates a wealth of statistical information in a compact format:
- The Box: This represents the interquartile range (IQR) between Q1 and Q3.
- The Median (Q2): A line inside the box indicates the median, which is the middle value of the dataset.
- The Whiskers: These extend from the box to show the range of the data outside of the middle half. They generally end at the smallest and largest data points, excluding outliers.
- Outliers: Points beyond the whiskers are potential outliers, usually marked with dots or asterisks.

Steps to Create a Box Plot

To effectively craft a box plot, follow these steps:
- Data Collection: Gather your data. Ensure it’s clean and suitable for analysis.
- Sorting: Arrange the data in ascending order to facilitate finding quartiles.
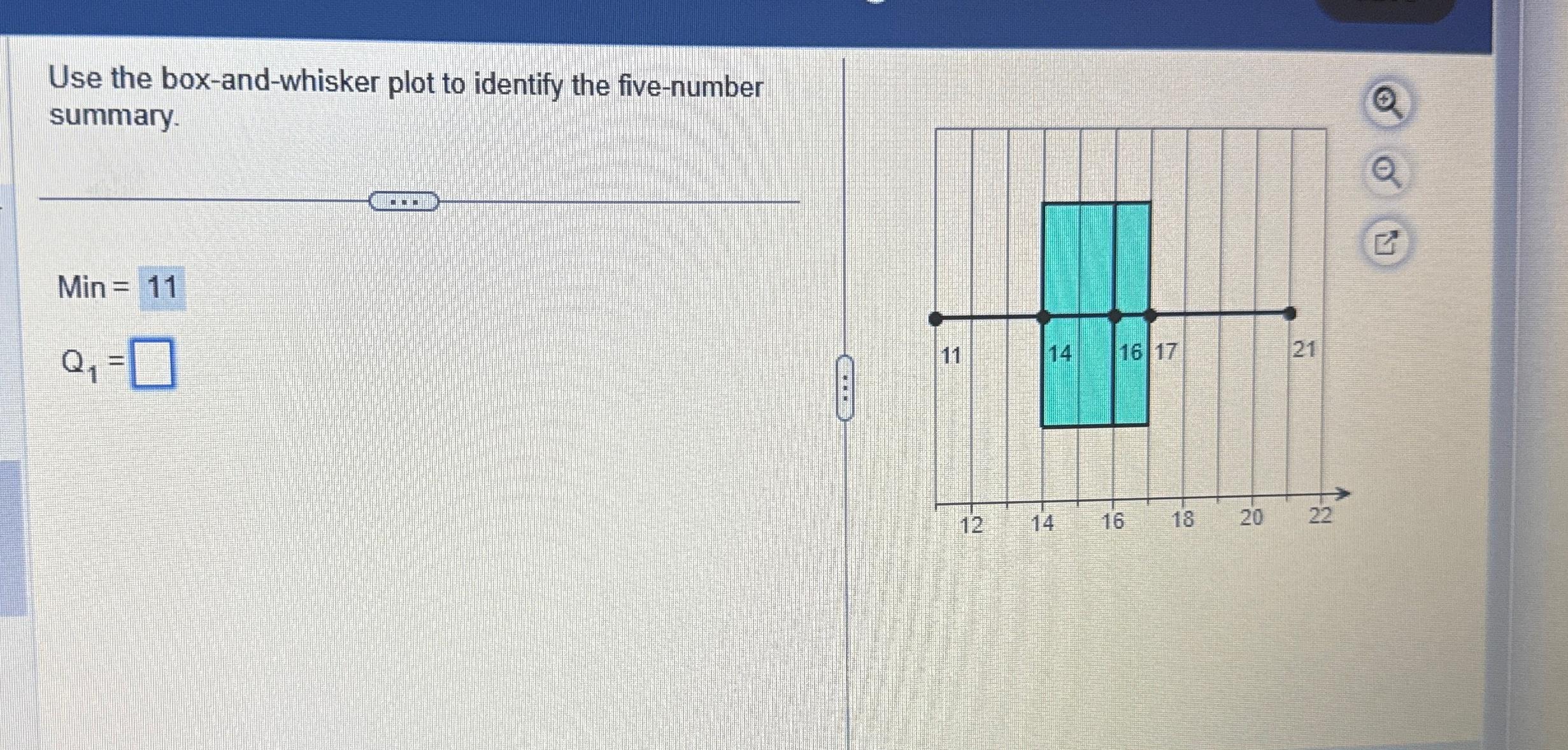
- Five-Number Summary: Calculate:
- Minimum: The smallest value in the dataset.
- Q1: The median of the lower half of the data.
- Median: The overall median value.
- Q3: The median of the upper half of the data.
- Maximum: The largest value in the dataset.
- Draw the Plot:
- Plot a horizontal or vertical line for each of the five summary statistics.
- Draw the box from Q1 to Q3.
- Place the median line inside the box.
- Extend whiskers from the box to the minimum and maximum values or to the furthest point within 1.5 times the IQR from the box edges, whichever is smaller.
- Identify and plot any outliers.
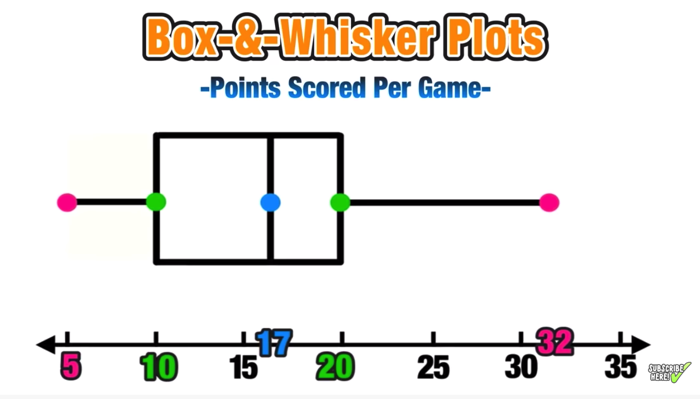
Example Calculation
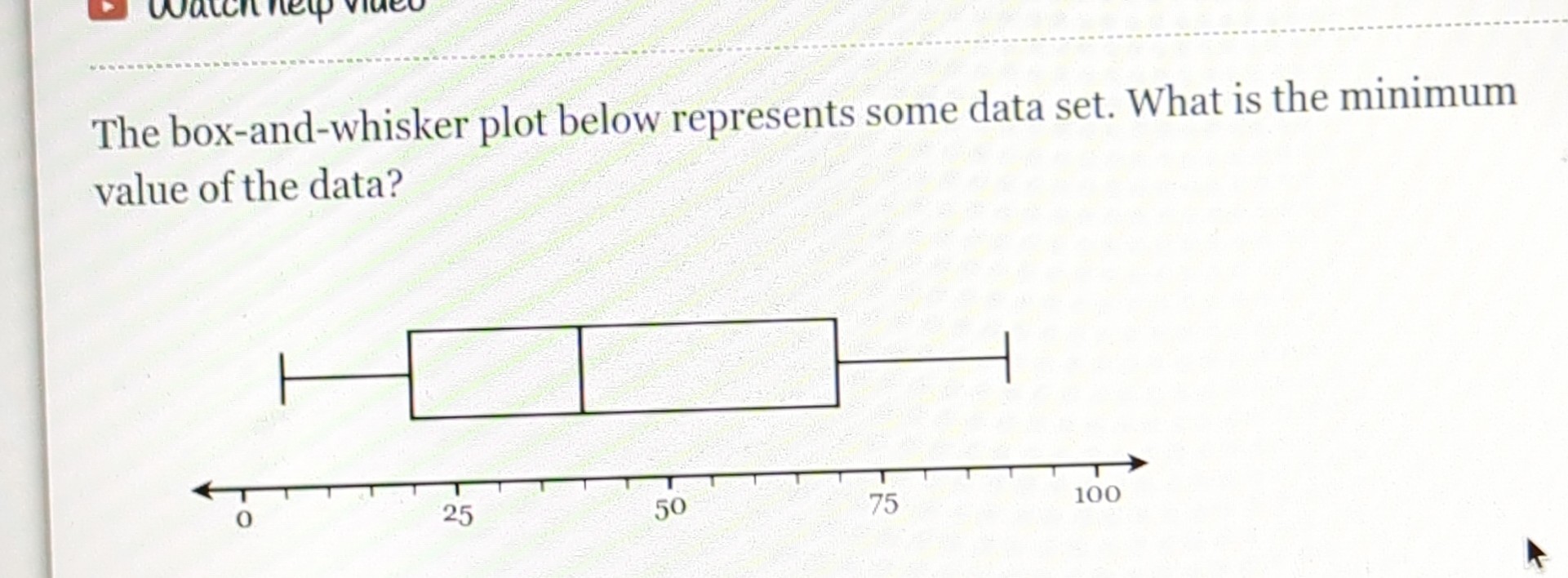
| Data | Value |
|---|---|
| Minimum | 5 |
| Q1 (First Quartile) | 12 |
| Median (Q2) | 18 |
| Q3 (Third Quartile) | 25 |
| Maximum | 30 |
🌟 Note: Remember to check for outliers when calculating the whiskers; outliers are values that fall beyond Q3 + 1.5 * IQR or Q1 - 1.5 * IQR.
Interpreting a Box Plot
- Median Position: The position of the median line within the box can reveal skewness. If it’s towards the lower end, the data skews left; if towards the upper end, it skews right.
- Box Width: A wider box indicates a larger IQR, meaning greater variability in the middle 50% of the data.
- Whisker Length: Longer whiskers suggest more spread in the data, potentially indicating a wider range of values or outliers.
- Outliers: These can suggest anomalies or errors in data collection but can also indicate natural variance or external factors affecting the data.
Each element of a box plot provides insight into the data's distribution, making it a powerful tool for descriptive statistics.
Applications of Box Plots
- Comparing Distributions: Box plots are excellent for comparing multiple groups or distributions side by side to understand differences in medians, quartiles, and spread.
- Data Analysis: They help in identifying the central tendency, dispersion, skewness, and any potential outliers or data anomalies.
- Data Visualization in Reporting: Box plots summarize complex datasets effectively, making them useful in reports, presentations, and publications where space is limited.
Advanced Box Plots

Beyond the basics, there are variations of box plots:
- Notched Box Plots: These have a notch or narrowing around the median, which provides a visual representation of the confidence interval around the median.
- Variability Box Plots: These show the variance or standard deviation inside the box, providing more detailed information on data spread.
- Bi-directional Box Plots: These display two sets of data on the same plot, often to compare pre-post conditions or paired data.
Understanding these variations expands the versatility of box plots in data analysis.
Creating Advanced Box Plots

The process for creating advanced box plots involves the same initial steps as creating basic box plots but includes:
- Statistical Adjustments: For notched box plots, calculate the width of the notch based on the median’s confidence interval.
- Additional Data Visualization: Incorporate additional statistical measures like mean or variance.
- Customization: Utilize different colors, line styles, and symbols to differentiate between multiple data sets on the same plot.
📌 Note: Notched box plots can be misleading if the sample size is small, as the notches will be wide, indicating less precision in median estimation.
Practical Examples

Here’s a quick look at how a box plot might help in different scenarios:
- Quality Control: Comparing the distribution of product dimensions from different manufacturing batches to identify consistency issues.
- Medical Research: Analyzing the spread of blood pressure readings across different patient groups to assess treatment effects.
- Financial Analysis: Visualizing the performance of stocks or funds over time, highlighting outliers or unusual market conditions.
In the above context, mastering box plots not only enhances your statistical toolkit but also sharpens your ability to interpret data with clarity and precision.
The power of box and whiskers plots lies in their ability to provide a snapshot of data distribution at a glance. Whether you're a student, a researcher, or a professional in data-driven fields, understanding and effectively using box plots will undoubtedly enrich your analytical capabilities. They offer a clear and concise way to communicate statistical findings, compare groups, and make data-driven decisions. With practice, you can unlock the full potential of these plots, making them an indispensable part of your data analysis repertoire.
What does the width of the box in a box plot represent?
+
The width of the box in a box plot represents the interquartile range (IQR), which is the distance between the first (Q1) and third quartiles (Q3). A wider box indicates greater variability in the middle 50% of the data.
Can box plots be used for ordinal data?

+
Yes, box plots can be used to visualize ordinal data, although they are most commonly used for interval or ratio data. The plot still provides insights into distribution, spread, and outliers.
How do you handle outliers in a box plot?
+
Outliers in box plots are typically defined as any data points that are more than 1.5 * IQR below Q1 or above Q3. They are often marked with a symbol (e.g., asterisk or dot) to indicate they are outside the expected range. Analysts can choose to exclude these from analysis, investigate them further, or adjust their methodology to account for them.