5 Ways to Master Box and Whisker Plots

When it comes to visualizing data distributions, box and whisker plots (or box plots) are indispensable tools in statistics. These plots offer a clear, concise way to understand the central tendency, variability, and outliers within your dataset. Mastering box and whisker plots not only enhances your ability to analyze data but also allows you to communicate complex statistical insights effectively. Let's explore five essential techniques to become proficient in using and interpreting these plots:
1. Understanding the Components of a Box Plot


Before diving into creating and analyzing box plots, it's crucial to understand what each part signifies:
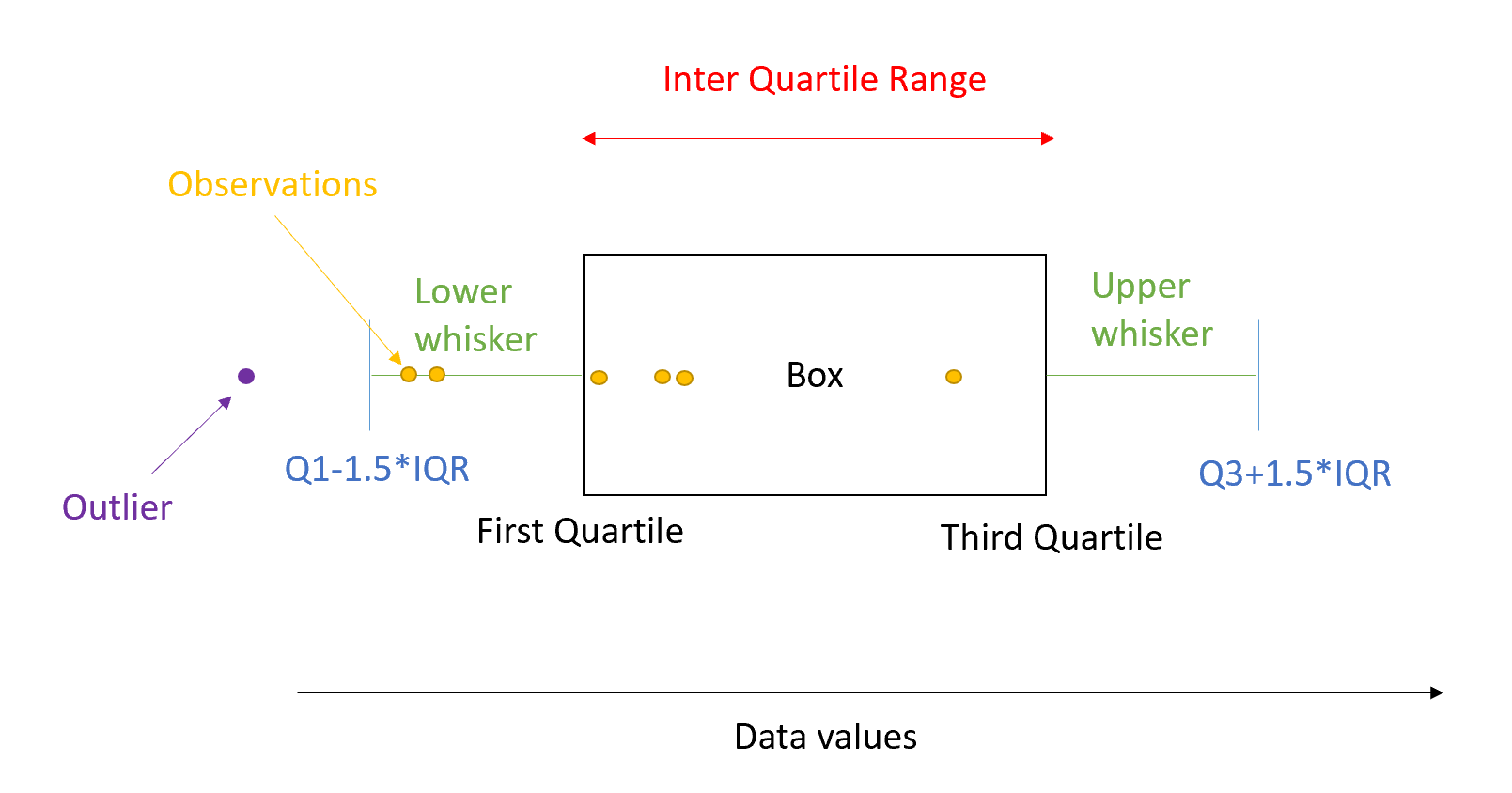
- Minimum (Min): The smallest data point within 1.5 * IQR (Interquartile Range) from the lower quartile.
- First Quartile (Q1): Represents the 25th percentile of the dataset.
- Median (Q2): The middle value, dividing the data into two halves.
- Third Quartile (Q3): Marks the 75th percentile, 75% of the data falls below this point.
- Maximum (Max): The largest data point within 1.5 * IQR from the upper quartile.
- Outliers: Data points outside the lower or upper whiskers.
- Interquartile Range (IQR): The distance between Q1 and Q3, indicating the spread of the middle 50% of the data.
- Whiskers: Extend from Q1 and Q3 to the smallest and largest non-outlier values.
🔍 Note: Understanding these components will make it easier to analyze and interpret data distributions.
2. Constructing a Box Plot
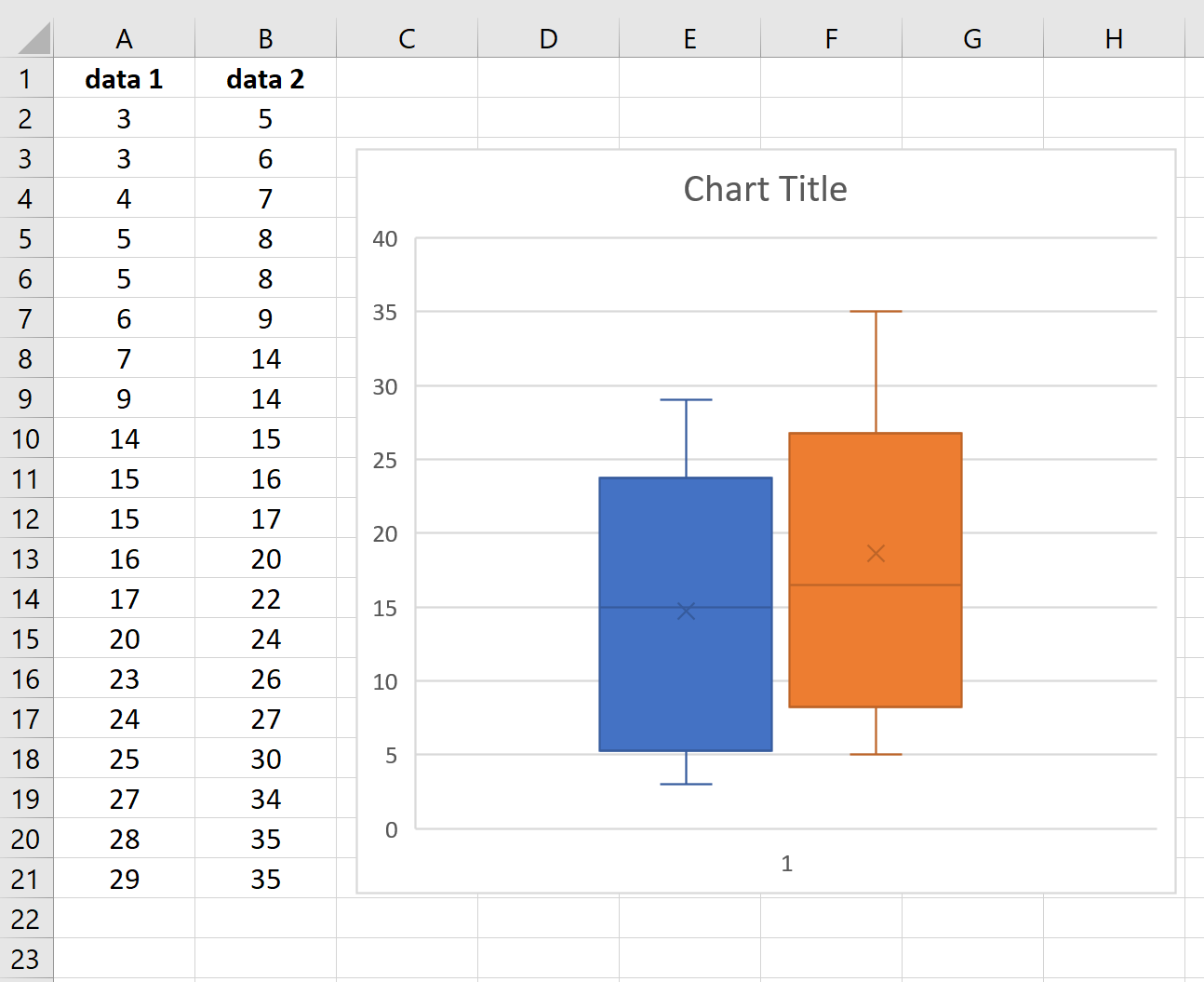

To construct a box plot, follow these steps:
- Data Collection: Gather or generate your dataset.
- Data Sorting: Arrange the data in ascending order.
- Find Quartiles: Determine Q1, median (Q2), and Q3.
- Identify the IQR: Subtract Q1 from Q3 to find the interquartile range.
- Calculate Whiskers: Use Q1 - 1.5 * IQR and Q3 + 1.5 * IQR to define the whisker endpoints.
- Identify Outliers: Any data point beyond the whiskers' range is considered an outlier.
- Draw the Box: Draw a rectangle (box) with the lower edge at Q1 and upper edge at Q3.
- Place the Median: Draw a line inside the box to represent the median.
- Extend Whiskers: Extend lines (whiskers) from the edges of the box to the smallest and largest data points within the calculated range.
- Mark Outliers: Plot outliers as individual points outside the whiskers.
💡 Note: Use software like R, Python (with libraries like matplotlib or seaborn), or even Excel to automate box plot construction for accuracy and speed.
3. Analyzing Skewness with Box Plots
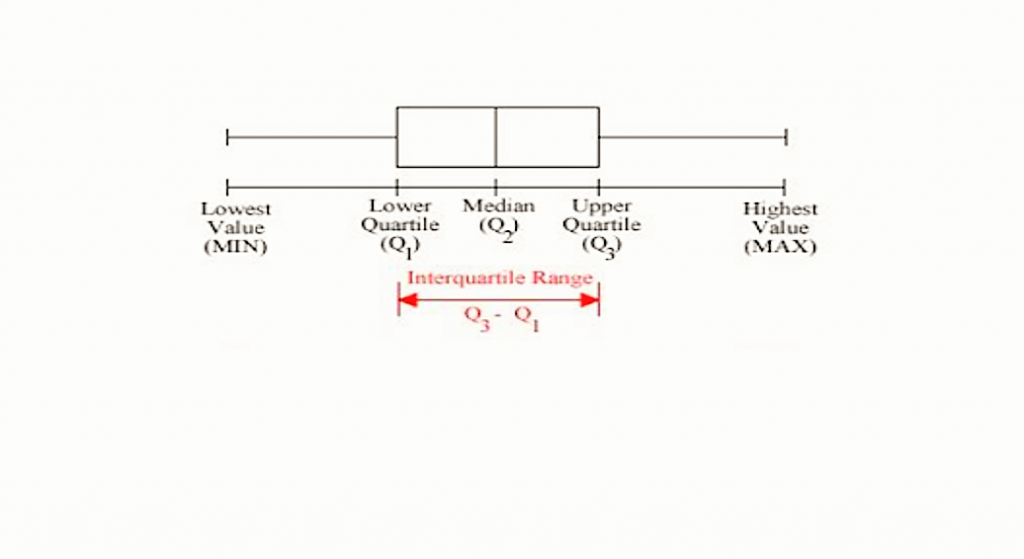

Box plots can quickly reveal the skewness of your data:
- Symmetric Distribution: The median is centrally located, and both whiskers extend equally.
- Right-Skewed (Positive Skew): The median is closer to Q1, and the right whisker is longer than the left one.
- Left-Skewed (Negative Skew): The median is nearer to Q3, with the left whisker being more extended.
Looking at the box's shape, length, and location of outliers, you can determine if the data is:
- Normally distributed.
- Positively skewed with potential right-tail outliers.
- Negatively skewed with left-tail outliers.
4. Comparing Multiple Datasets


Box plots shine when comparing two or more datasets:
- Visualize Variance: Compare the spread (IQR) between different groups.
- Identify Medians: Quickly determine which group has the higher median.
- Assess Outliers: Determine if some groups have more or different types of outliers.
- Observe Overlap: Check for data overlap, which might suggest homogeneity between groups.
| Dataset | Median | IQR | Outliers |
|---|---|---|---|
| A | 25 | 10 | 2 outliers above |
| B | 35 | 15 | 1 outlier below |

👀 Note: Use side-by-side or overlaid box plots for better comparison.
5. Beyond the Basics: Enhancements and Variations


To further master box plots, explore these enhancements:
- Notched Box Plots: Adding notches helps in visually assessing if the medians of two groups differ significantly.
- Violin Plots: Combine box plots with kernel density plots for a fuller picture of data distribution.
- Error Bars: Add error bars to indicate variability and confidence intervals.
- Categorical Variables: Use box plots within facets or split by categorical variables for group-specific insights.
- Adjust for Outliers: Modify whiskers or show separate data points to handle outliers differently.
🌟 Note: Each enhancement can provide additional layers of information, but use them judiciously to avoid clutter.
By mastering these five techniques, you can go beyond mere creation and delve into the interpretation of box plots. Whether you're comparing datasets, assessing distribution characteristics, or presenting complex statistical insights, box plots provide a graphical summary that can be instantly comprehended. From understanding basic components to employing advanced variations, these methods equip you with the tools needed to unlock the full potential of your data analysis efforts. Remember, the key to effective data visualization and interpretation lies not just in the construction of the plot, but also in its thoughtful application to reveal underlying patterns and anomalies in your data.
What is the difference between Q1, median, and Q3?

+
Q1, or the first quartile, represents the 25th percentile of the data, meaning 25% of the data points fall below this value. The median (Q2) is the middle value, dividing the dataset into two equal parts. Q3, the third quartile, marks the 75th percentile, with 75% of the data falling below this point. Essentially, Q1 and Q3 define the lower and upper bounds of the middle 50% of the dataset, respectively, while the median is its central point.
How can box plots help in detecting outliers?

+
Box plots are excellent for identifying outliers because any data point outside of the whiskers’ range (which is defined as 1.5 * IQR from Q1 or Q3) is considered an outlier. These points are often plotted as individual dots outside the box and whiskers, making it visually apparent when extreme values exist in the dataset.
Why is the Interquartile Range important in box plots?

+
The Interquartile Range (IQR) is crucial because it defines the spread of the middle 50% of the data, providing a measure of statistical dispersion that is less affected by outliers than the standard deviation or range. It helps to determine the length of the box in the plot, indicating the variability of the data. Additionally, IQR is used to calculate the position of the whiskers and to identify outliers.
Can you use box plots for time series data?
+
Yes, you can use box plots to visualize time series data, especially if you’re looking to analyze how the distribution of data changes over time. For example, you could plot monthly or yearly data to see shifts in central tendency, variability, and outliers over time. Each box plot would represent the distribution for a specific time period.
Are there any alternatives to box plots for showing data distribution?

+
Yes, some alternatives include:
- Violin Plots: Combine a box plot with a kernel density plot to show distribution shape and variability.
- Histograms: Binned frequency distributions to visualize data spread and shape.
- Density Plots: Similar to histograms but smoother, showing the probability density function.
- Q-Q Plots (Quantile-Quantile Plots): Compare your data to a theoretical distribution like the normal distribution.
Each has its strengths, and choosing the right one depends on what aspect of the data distribution you want to highlight.



