Mastering Basic Probability: Free Worksheet Inside

Understanding the basic concepts of probability is essential for anyone venturing into statistics, data analysis, or even for those who enjoy strategic games like poker or betting on sports. Whether you are a student trying to grasp the fundamentals or a professional refining your analytical skills, this guide aims to provide you with a deep dive into the fascinating world of probability.
What is Probability?

Probability can be defined as the measure of the likelihood that an event will occur. It's all about predicting the chances of an event, ranging from 0 to 1 where:
- 0 signifies that the event is impossible.
- 1 means the event is certain to happen.
Here's how you calculate probability:
P(E) = Number of Favorable Outcomes / Total Number of Possible Outcomes
Why is Understanding Probability Important?

Mastering the basics of probability:
- Aids in decision-making in various life scenarios.
- Enhances your skills in fields like finance, gambling, weather forecasting, and health analysis.
- Forms the foundation for advanced statistical concepts.
Key Terms in Probability
Here's a table to help you understand some of the key terminology:
| Term | Definition |
|---|---|
| Event | An outcome or set of outcomes of an experiment or trial. |
| Sample Space | The set of all possible outcomes or results from a probability experiment. |
| Outcome | A single result from the sample space of an experiment. |
| Probability | The numerical measure of the chance of an event happening. |

🤔 Note: Remember that probability does not deal with certainty; it gives us a measure of likelihood, which can sometimes be misleading if not understood correctly.
How to Calculate Simple Probabilities

Here's how you can calculate the probability for different types of events:
Single Event Probability

If you roll a fair six-sided die, what’s the probability of rolling a 4?
P(rolling a 4) = 1 / 6 = 0.1667 or about 16.67%
Mutually Exclusive Events

When events can’t occur at the same time, you add their probabilities:
P(E1 or E2) = P(E1) + P(E2)
Non-Mutually Exclusive Events

When events can happen simultaneously, you subtract the overlap:
P(E1 or E2) = P(E1) + P(E2) - P(E1 and E2)
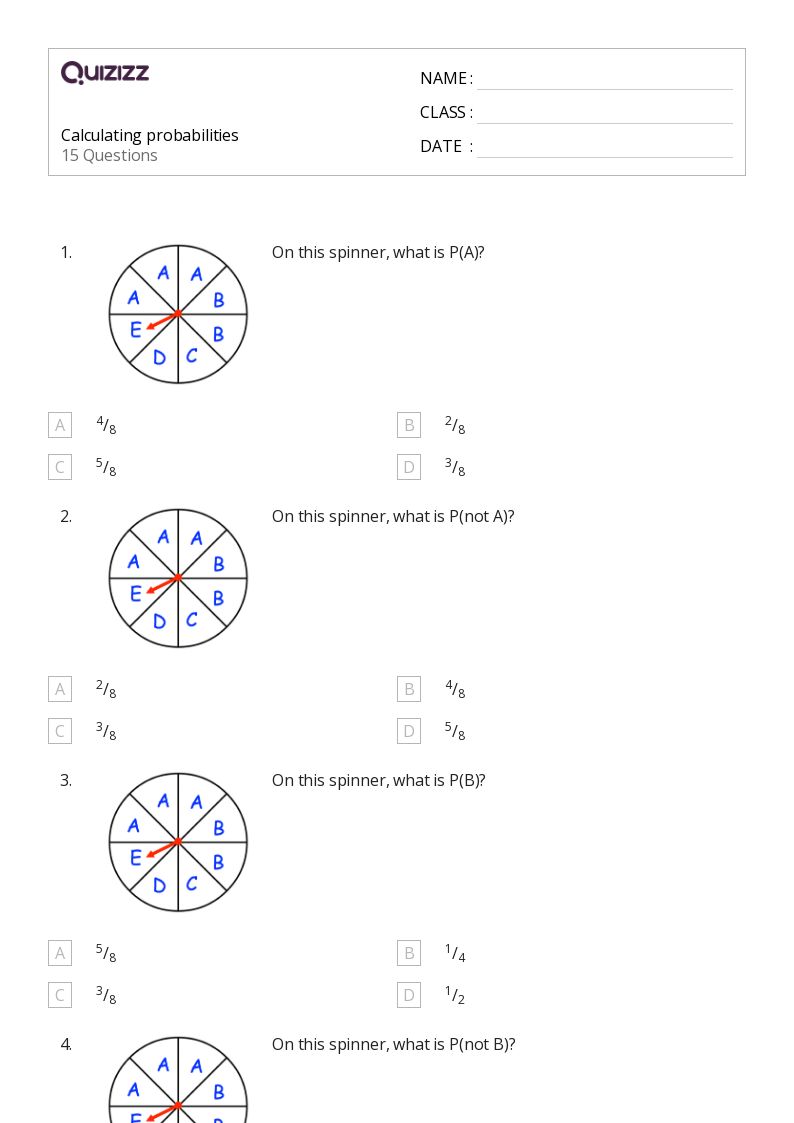
Downloadable Probability Worksheet

Enhance your understanding with our free probability worksheet:
Advanced Concepts in Probability

Let's delve into some more complex probability concepts:
Conditional Probability

This is the probability of an event occurring given that another event has already happened:
P(A given B) = P(A and B) / P(B)
Bayes’ Theorem

Bayes’ Theorem helps update the probability of a hypothesis based on new evidence:
P(A | B) = [P(B | A) * P(A)] / P(B)
Independence

Two events are independent if the occurrence of one doesn’t affect the other:
P(A and B) = P(A) * P(B)
🧠 Note: Independence can be a tricky concept. Always test for independence before assuming two events are independent.
Real-World Applications of Probability

Here are some scenarios where probability shines:
Gambling

- Casinos use probability to manage risk and profitability.
- Gamblers calculate odds to make strategic bets.
Health

- Probabilities help in calculating the likelihood of disease or survival rates.
- Used in diagnostics for interpreting test results.
Business and Finance
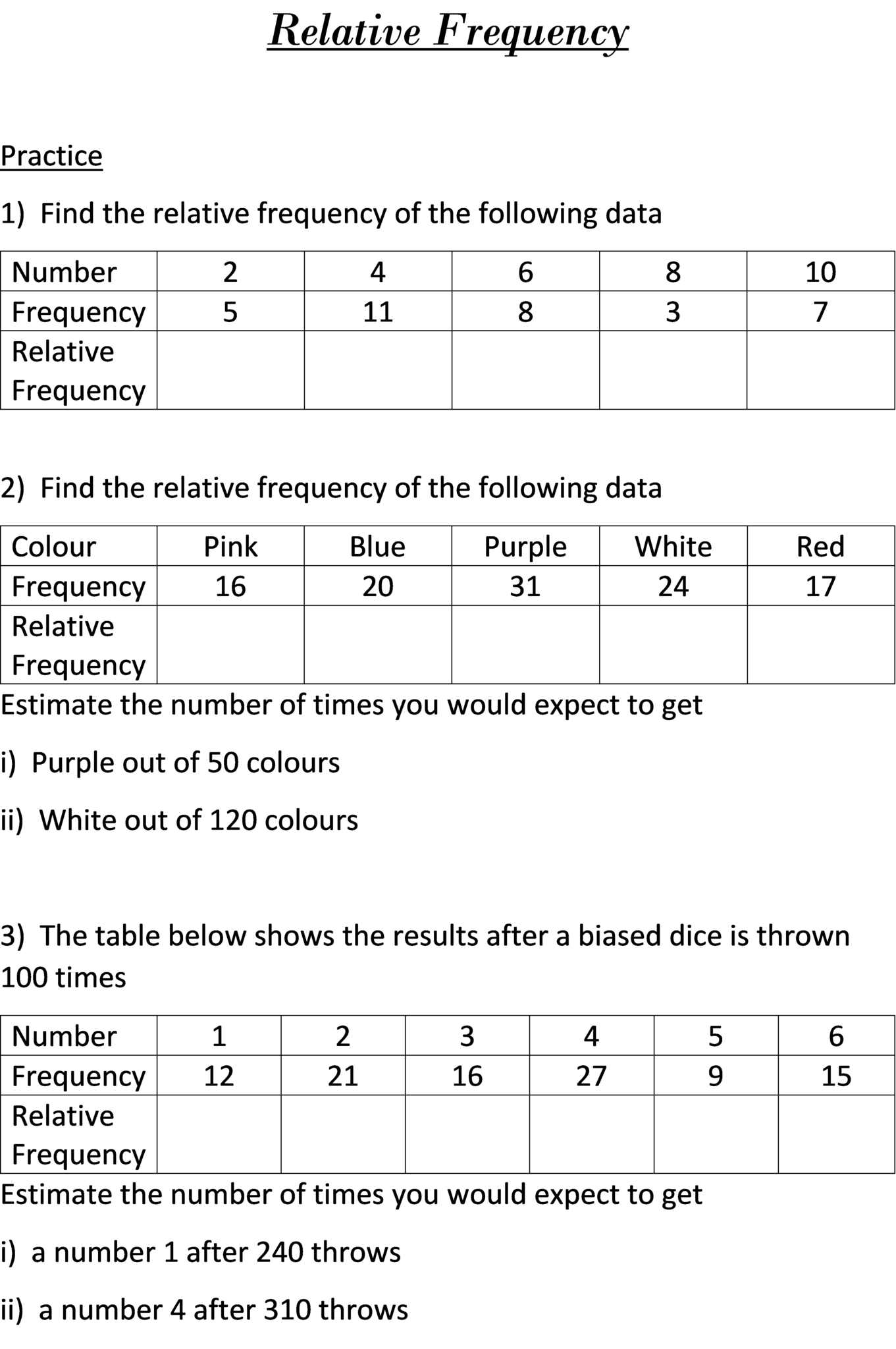
- Probability models are used for stock market forecasting.
- Helps in making risk assessments.
Final Thoughts

Understanding probability not only makes you better at predicting outcomes but also enriches your decision-making process in daily life. From the simple coin toss to the complex weather forecasting models, probability is all around us. As you continue to explore this fascinating field, remember that probability is a tool to aid understanding, not a guarantee of future events. Each step in learning probability equips you with better insight into how the world functions at a fundamental level.
What is the difference between probability and odds?

+
Probability is the likelihood of an event occurring, expressed as a fraction or decimal between 0 and 1. Odds, on the other hand, compare the likelihood of an event to the likelihood of it not happening. For example, the probability of flipping heads on a coin is 0.5 or 1/2, whereas the odds would be 1 to 1 or simply "even" odds.
How can one improve their understanding of probability?
+Practice is key. Work through probability problems, understand real-world applications, and use tools like probability calculators or simulations to visualize concepts. Also, learning probability through practical exercises like games of chance can make the subject more intuitive.
Can probability tell us what will definitely happen?
+No, probability provides a measure of the likelihood, not certainty. Even with a 99% chance, an event can still not happen, and with a 1% chance, it can occur. Probability deals with chances, not absolute outcomes.