Mastering Basic Fractions: Free Worksheet and Tips

Understanding fractions is a fundamental skill in mathematics that is crucial for progressing in more advanced areas of study, like algebra and calculus. Despite their basic appearance, fractions form the backbone of many mathematical concepts and real-life scenarios, from cooking to financial planning. In this detailed exploration, we will delve into what fractions are, how they work, and provide a free worksheet that you can use to practice and master basic fraction skills.
What Are Fractions?
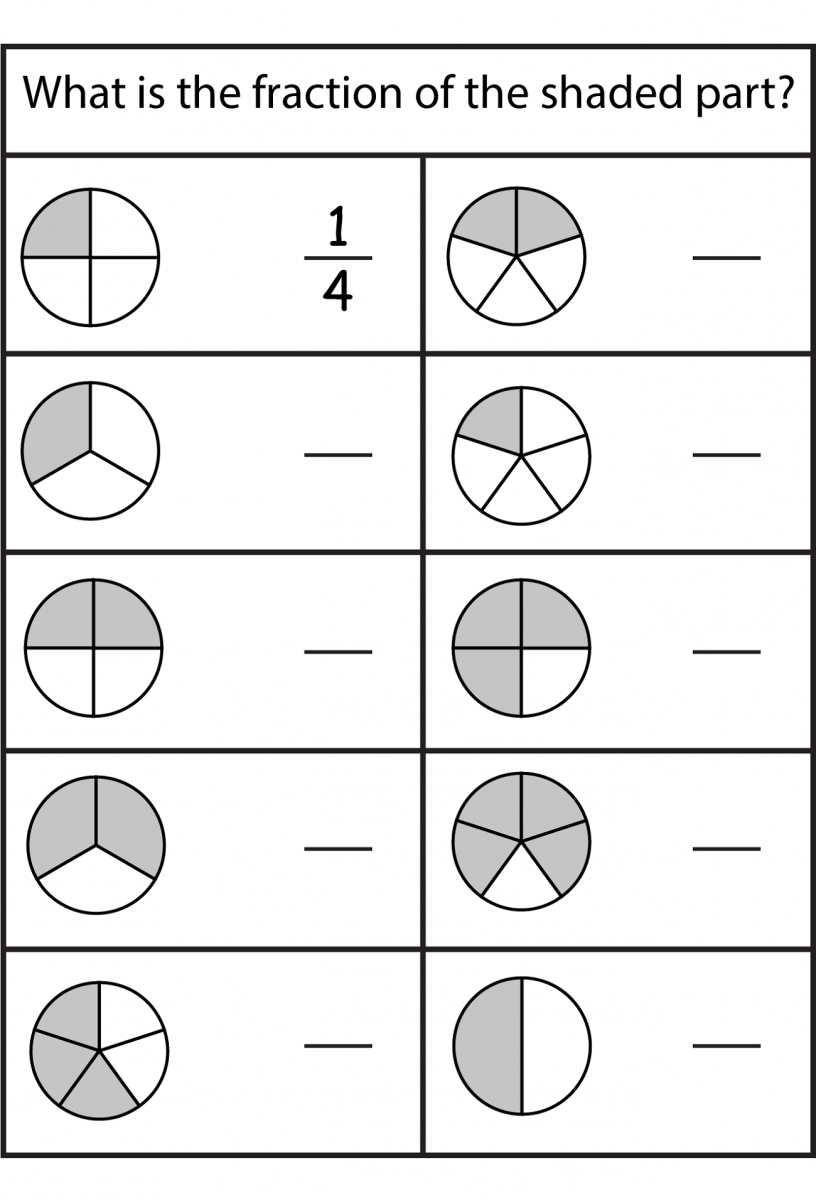
A fraction represents a part of a whole. It consists of two numbers separated by a horizontal or diagonal line, known as the numerator and the denominator:
- Numerator: The top number, indicating the number of parts you have.
- Denominator: The bottom number, indicating the total number of equal parts into which the whole has been divided.
Types of Fractions

Proper Fractions

These are fractions where the numerator is less than the denominator, like 3⁄4 or 2⁄5.
Improper Fractions

In these, the numerator is equal to or greater than the denominator, for example, 5⁄4 or 12⁄7.
Mixed Numbers

A mixed number combines a whole number with a proper fraction, like 1 3⁄4. Here, the 1 is a whole number, and 3⁄4 is a fraction.
The Importance of Fractions

Fractions are not just an academic exercise; they appear in many practical applications:
- Cooking and Baking: Recipes often require you to measure ingredients in fractions.
- Finance: Understanding ratios, interest rates, and financial planning often involves working with fractions.
- Time: Telling time using an analog clock involves fractional understanding of hours and minutes.
- Statistics: Analyzing data frequently requires understanding fractions and percentages.
How to Work with Fractions
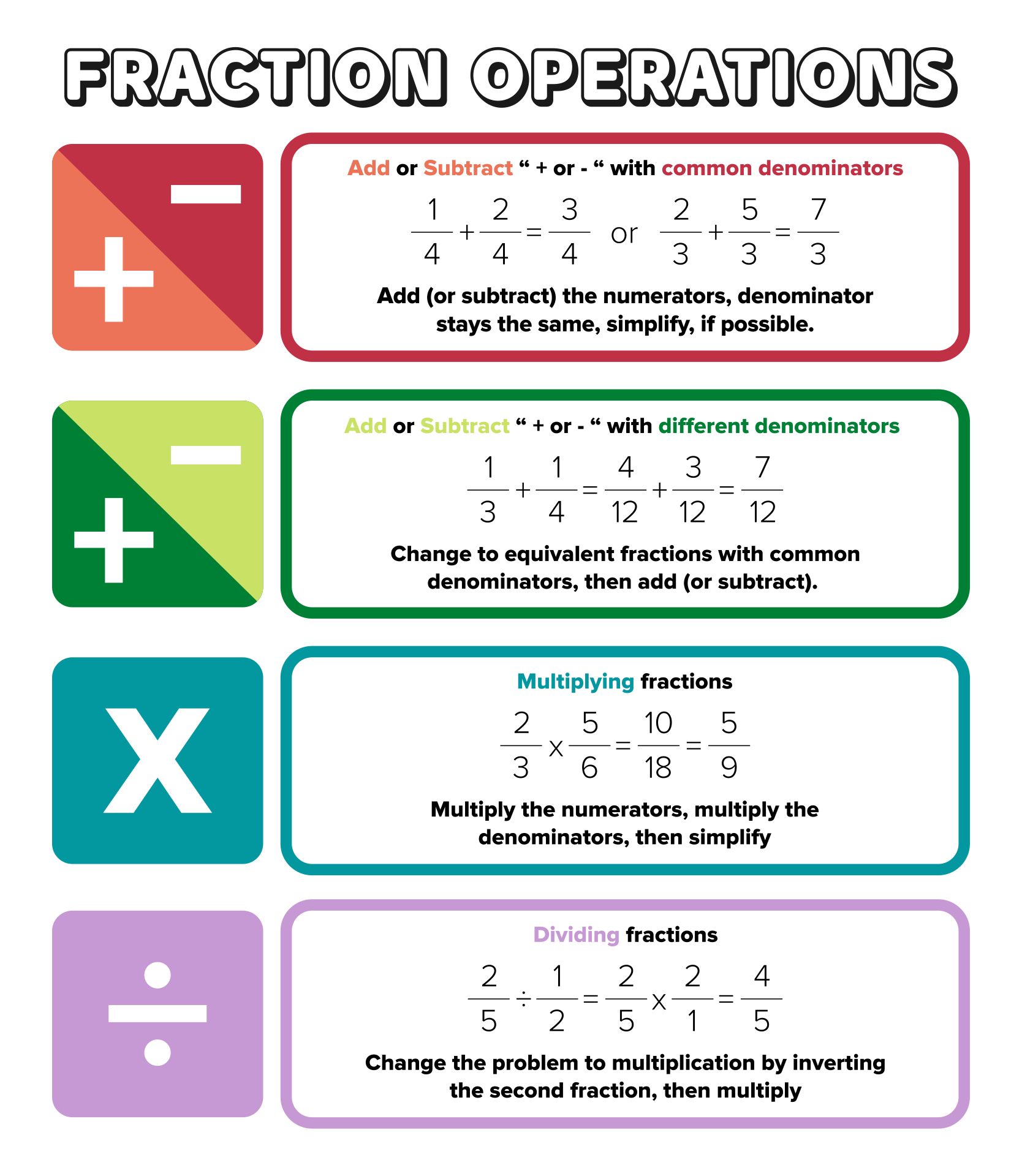
Adding and Subtracting Fractions

Adding or subtracting fractions involves the following steps:
- If the denominators are different, find the least common multiple (LCM) of these denominators.
- Convert each fraction to have this common denominator.
- Add or subtract the numerators as necessary.
- Reduce the fraction if possible.
Multiplying and Dividing Fractions

These operations are simpler:
- Multiplication: Multiply the numerators together, then the denominators, and reduce if possible.
- Division: Multiply by the reciprocal of the second fraction (flip the second fraction).
Converting Between Fractions and Mixed Numbers

To convert an improper fraction to a mixed number:
- Divide the numerator by the denominator.
- The quotient is the whole number part, and the remainder becomes the numerator of the fraction, with the same denominator.
Conversely, to convert a mixed number to an improper fraction:
- Multiply the whole number by the denominator.
- Add the result to the numerator.
- Place this over the original denominator.
Practical Applications
Division as Fractions
Any division problem can be expressed as a fraction. For example, 5 divided by 3 is written as 5⁄3. This simple trick helps in quickly converting between division and fractional representations.
Fractions in Measurements
When dealing with measurements, especially in areas like construction or sewing, understanding how to add, subtract, or simplify fractions can be invaluable. Here’s an example:
| Wood Lengths | Original | Converted |
|---|---|---|
| Cut 1 | 2/3 ft | 8/12 ft |
| Cut 2 | 3/4 ft | 9/12 ft |
| Total Cut | 5/12 ft | 5/12 ft |

⚠️ Note: Always simplify fractions before using them in practical applications for clarity and simplicity.
How to Learn and Master Fractions

Learning fractions can seem daunting at first, but with the right approach, anyone can master them:
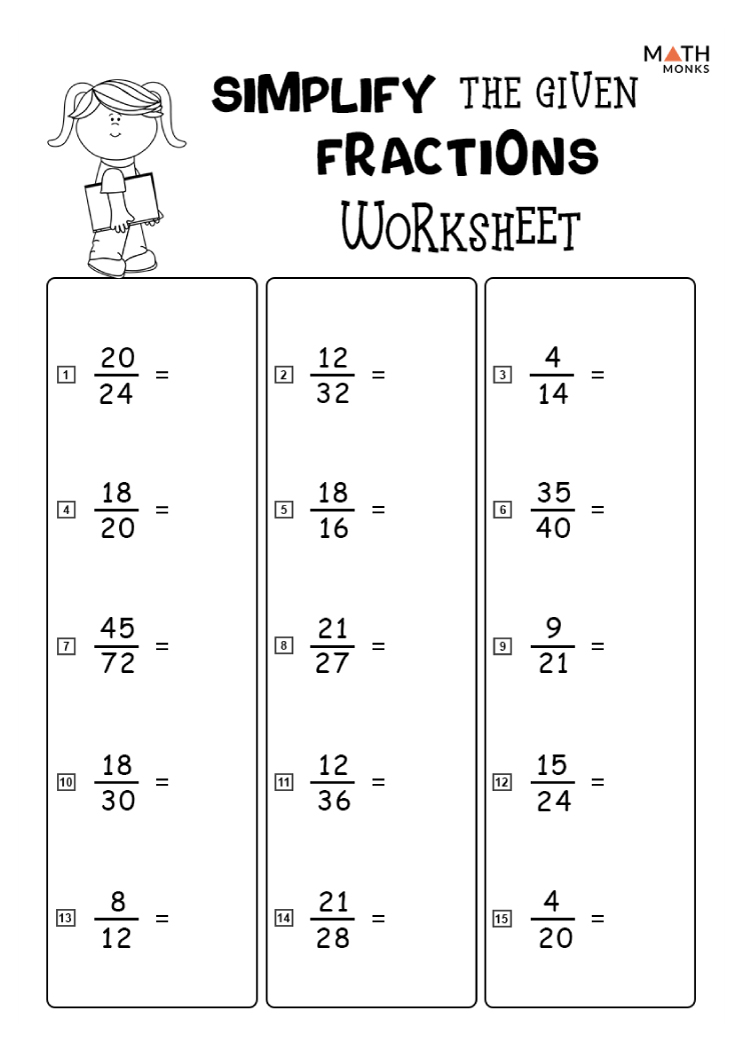
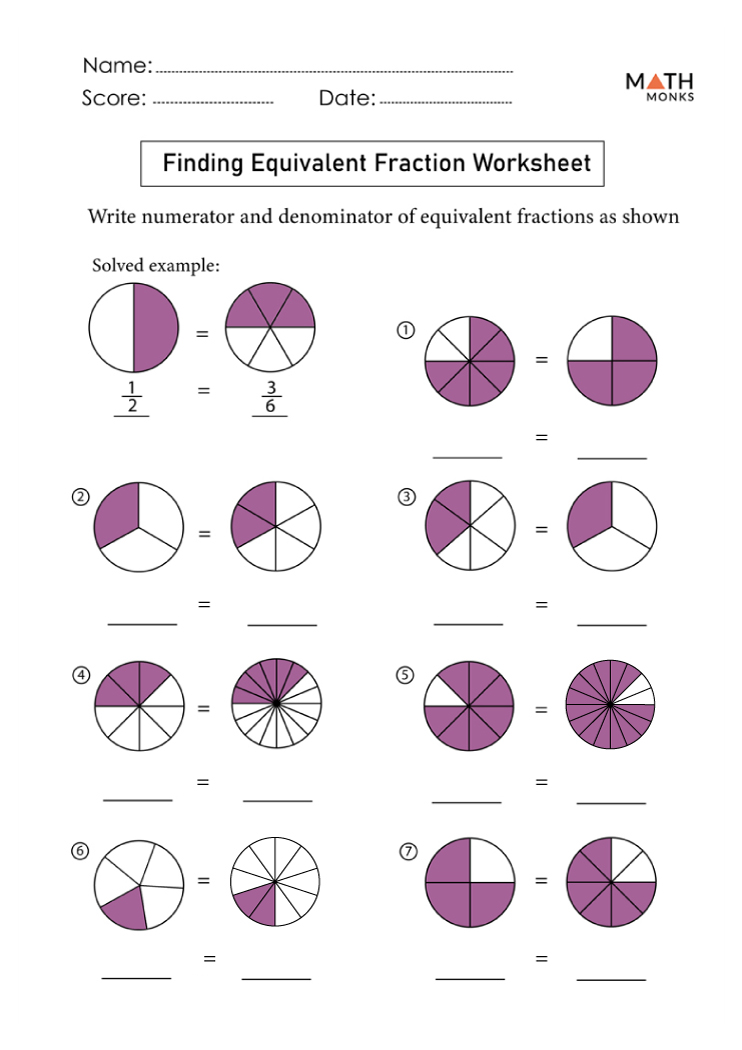
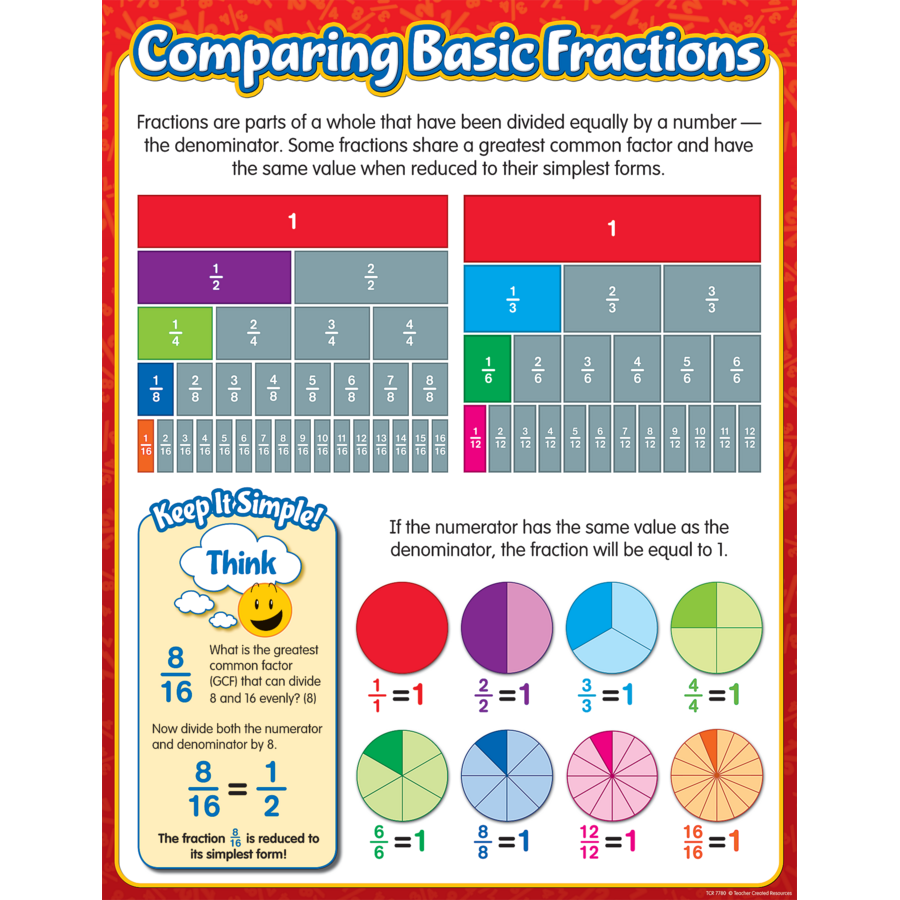
- Use Visual Aids: Fraction bars, number lines, and pie charts can be incredibly helpful in understanding fractions visually.
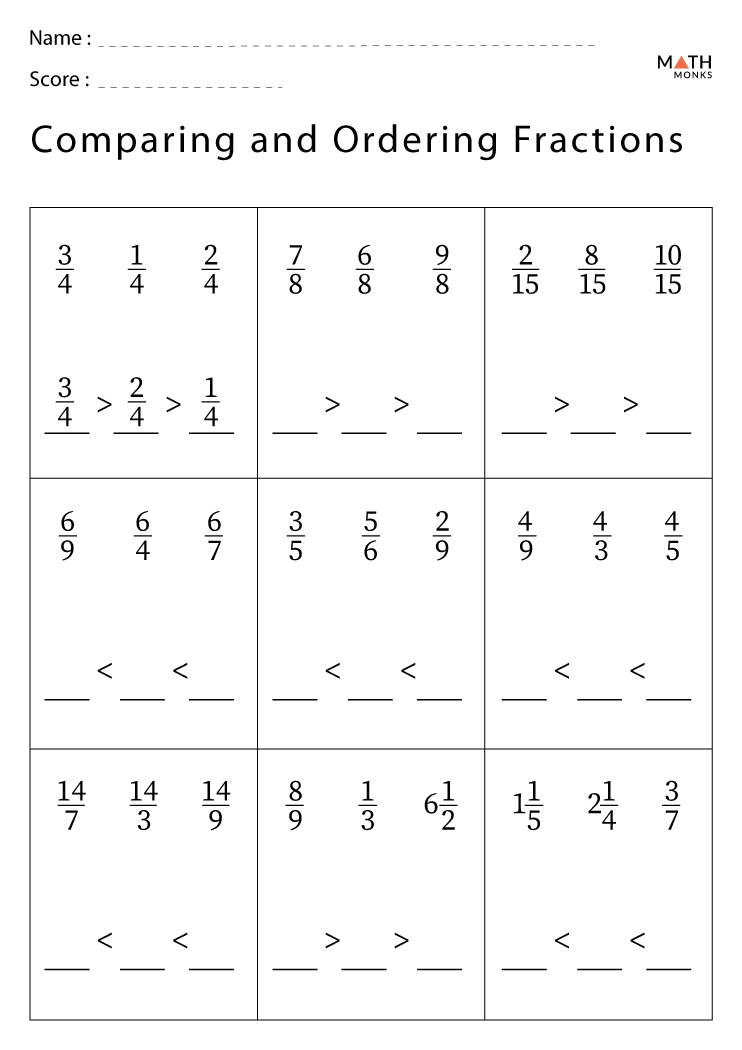
- Practice: Use worksheets or practice problems that focus on real-life scenarios.
- Games and Activities: Incorporating learning into games or fun activities can make the learning process engaging.
- Understand Concepts: Grasp the meaning behind operations; for example, multiplying fractions means taking a part of a part.
Final Thoughts

Understanding fractions is not just about mastering a part of mathematics; it’s about equipping oneself with the tools to navigate through daily life more effectively. By understanding how to manipulate fractions, you open up a world of practical applications, from cooking to financial management. Remember, practice makes perfect, and with the provided worksheet, you have an opportunity to cement your understanding of fractions. Keep refining your skills, and you’ll find that fractions are not only manageable but incredibly useful in enhancing your mathematical acumen and real-world problem-solving abilities.
What is the difference between a proper and improper fraction?
+
A proper fraction has a numerator smaller than its denominator, whereas an improper fraction has a numerator equal to or larger than its denominator. A mixed number, which combines a whole number with a proper fraction, is another way to represent the improper fraction.
Why do we need fractions?

+
Fractions are essential in a wide range of applications, including mathematics, finance, measurements, cooking, and even time management. They help us represent and work with quantities that are not whole numbers.
How can I simplify my life using fractions?
+By understanding fractions, you can manage recipes, budgets, time, and measurements more efficiently. It simplifies complex division problems, allows you to deal with partial quantities, and provides a foundation for understanding more complex math concepts like ratios and proportions.