5 Easy Worksheets to Master Basic Area Calculations

Understanding how to calculate the area of different shapes is fundamental not just in mathematics but in numerous practical applications, from architecture to interior design. Whether you're a student, teacher, or simply an enthusiast looking to refresh your skills, mastering basic area calculations can provide both utility and satisfaction. In this blog post, we'll explore five easy worksheets designed to help you or your students master the concept of area calculations.
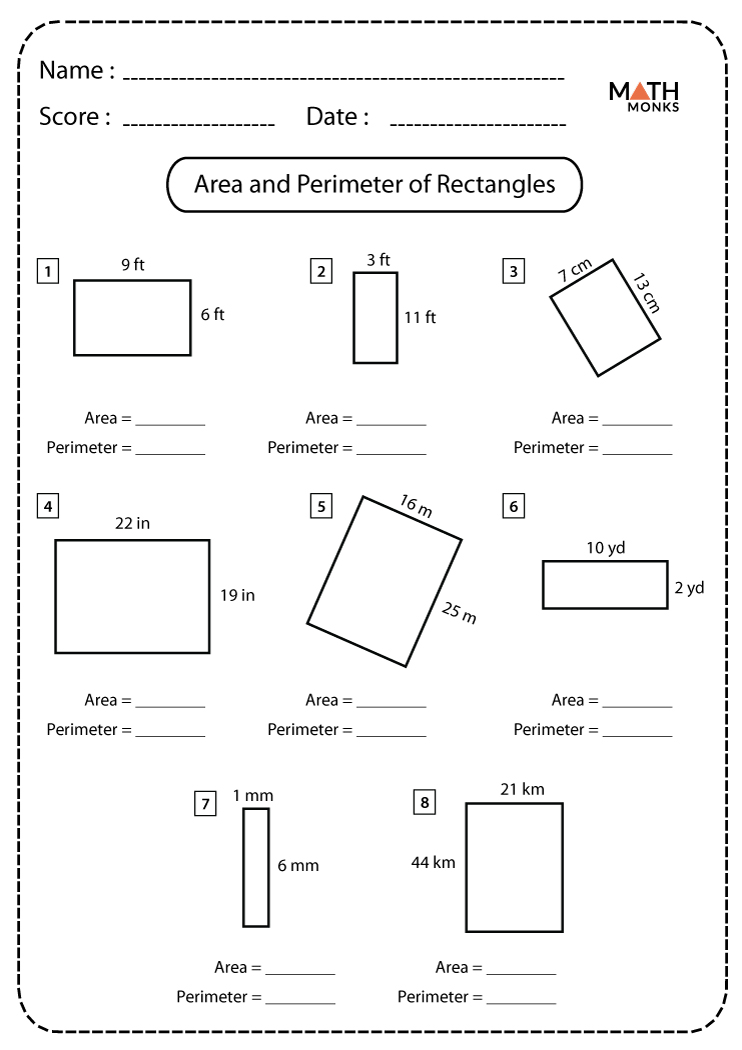
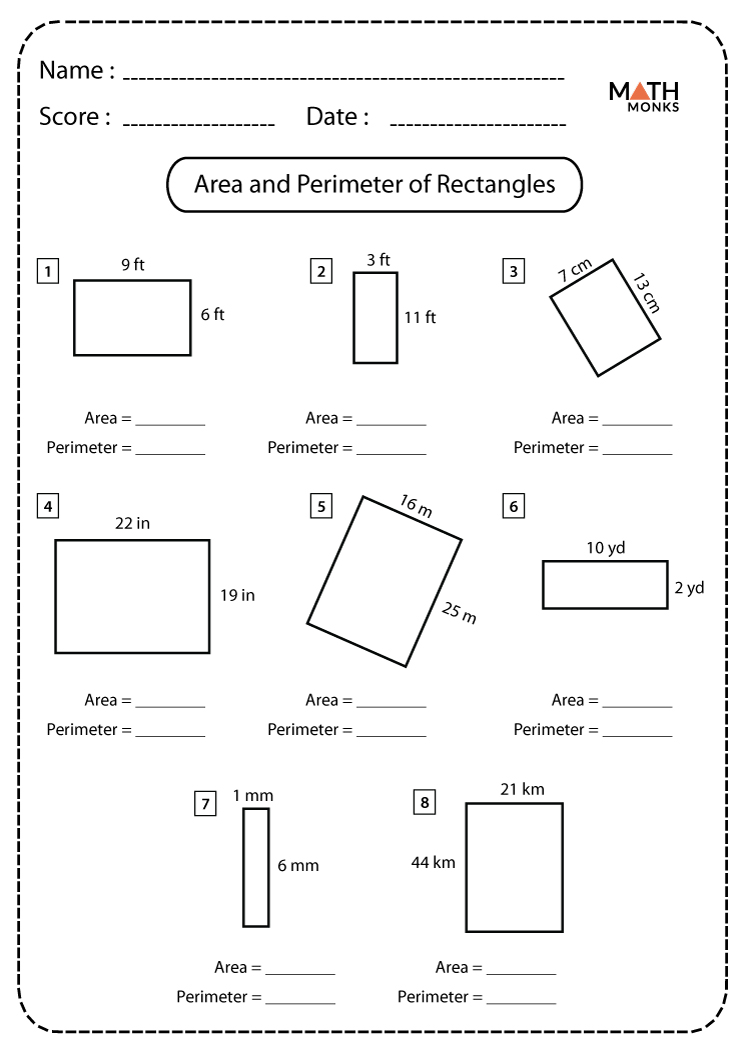
Worksheet 1: Understanding Rectangles and Squares


Objective: Familiarize with the simplest shapes where area calculation is straightforward.
- Calculate the area of given rectangles and squares.
- Fill in missing sides with the given area.
- Create shapes with specific areas.
Understanding that the area of a rectangle or square is calculated as length times width is crucial. This worksheet starts with easy examples where all dimensions are provided, moving to more complex problems where only the area or some sides are known.
📘 Note: The formula for area of a square is A = s², where s is the side length. For rectangles, it's A = l × w.
Worksheet 2: Triangles and Parallelograms


Objective: Expand knowledge to shapes with slightly more complex area formulas.
- Identify base and height.
- Calculate area using the formula A = (b × h) / 2 for triangles and A = b × h for parallelograms.
- Compare areas of similar shapes.
These shapes introduce students to the concept of using half of the product for triangles and understanding that parallelograms are essentially “sideways” rectangles when it comes to area calculation.
🌟 Note: Always measure the perpendicular height, not the slanted side in triangles and parallelograms.
Worksheet 3: Circles and Semi-Circles

Objective: Introduce the use of π (pi) in area calculations.
- Calculate the area of circles using A = πr².
- Find the radius given the area.
- Understand and calculate the area of semi-circles.
Here, students will work with approximations of pi, learning to round their answers appropriately and deal with real-life applications where circular measurements are common.
📐 Note: The value of π is typically taken as 3.14 for simplicity in these exercises.
Worksheet 4: Composite Figures

Objective: Apply knowledge of different shapes’ areas to calculate composite or irregular figures.
- Divide complex shapes into known shapes.
- Calculate the area of each part.
- Add or subtract areas to find the total.
This worksheet challenges students to think beyond isolated shapes and apply their understanding to more practical and complex scenarios.
Worksheet 5: Mixed Problems


Objective: Consolidate learning with a mix of all previously discussed shapes.
- Multi-step problems involving multiple shapes.
- Problems where additional calculations (like perimeter) might be needed to solve area.
- Challenge questions to test analytical skills.
Mastering this worksheet shows a well-rounded understanding of area calculations, which prepares learners for real-world applications where shape dimensions and areas are not always straightforward.
In conclusion, these worksheets provide a structured path for learning and mastering basic area calculations. They cater to different learning levels and increase in complexity, ensuring progressive learning. Remember, the key to mastering any mathematical concept lies in consistent practice, understanding the underlying principles, and applying them in varied contexts. Whether it’s for personal improvement or educational purposes, these worksheets will prove invaluable.
Why is it important to learn about areas?

+
Understanding areas is essential for fields like engineering, construction, painting, and even basic household tasks. It helps in estimating materials needed, cost, space requirements, and much more.
What if I struggle with the π (pi) calculations?
+
Use a calculator or a π constant in your calculations. For educational purposes, understanding that π is approximately 3.14 is enough for basic calculations. With practice, handling π becomes easier.
Can these worksheets be adapted for advanced learners?

+
Absolutely. You can introduce variables, require more precise calculations, or involve more complex shapes and formulas like ellipses or sectors of a circle.
How can these worksheets help in real-life scenarios?

+
They can be directly applied in planning and executing projects, from landscaping to understanding how much paint to buy for a room, or how much fabric for a dress. They foster practical mathematical thinking.
Is there an ideal order to complete these worksheets?

+
Yes, starting from the basic shapes in Worksheet 1 and progressing to the mixed problems in Worksheet 5 provides a logical progression of difficulty and complexity.



