5 Quick Tips for Calculating Shaded Region Areas

Understanding the Basics of Shaded Region Area Calculation

The task of calculating shaded region areas is a common challenge in both geometry and real-world applications. Whether you're a student working on a geometry problem or an engineer needing precise area calculations, understanding the principles behind these calculations can significantly enhance your problem-solving skills. Here are five quick tips to get you started:
Tip #1: Visualize the Problem
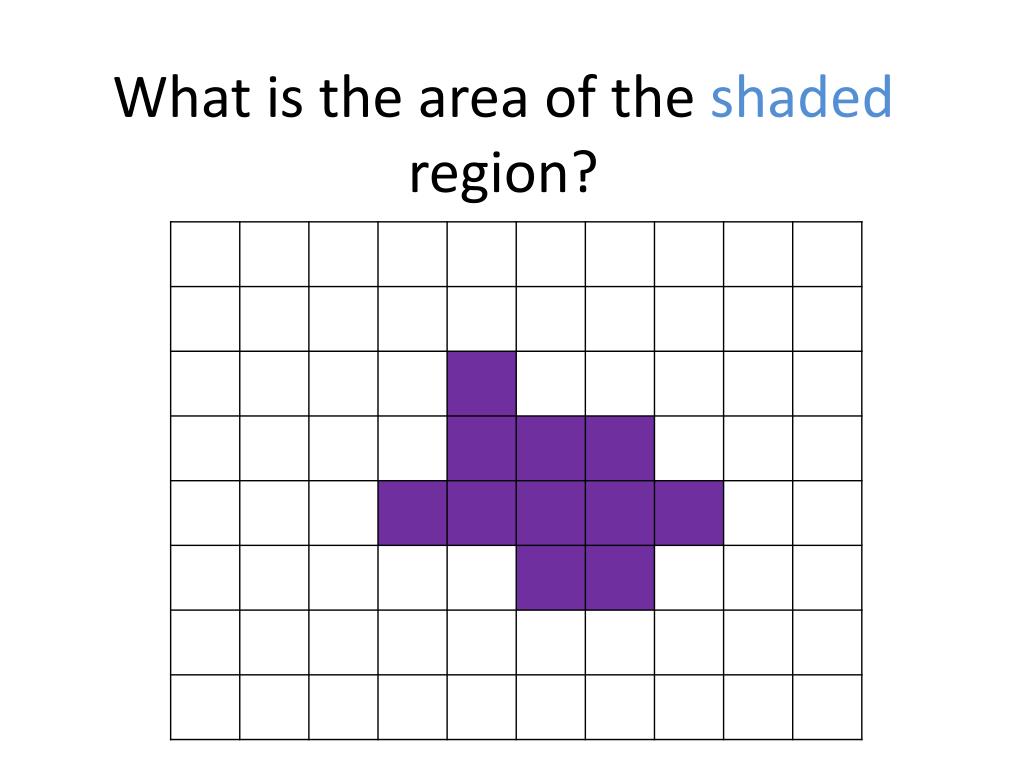
Before diving into complex mathematical formulas, take a moment to visualize the problem. Drawing a clear diagram can help you:
- Identify the shape of the shaded area.
- Recognize the relationship between different geometric figures.
- Spot any simpler shapes that can be used for easier calculations.
🔍 Note: Always label your diagram with all known dimensions and variables to make calculations more manageable.
Tip #2: Divide and Conquer

Often, shaded regions are not simple shapes but rather the difference or sum of simpler shapes:
- Identify if the shaded region is the result of subtracting one shape from another.
- Use integration for regions under curves, dividing the area into strips or rectangles.
- Understand the intersection of circles or other curves to find unique shapes.
Here's a simple example:
| Shape | Area | Shaded Region |
|---|---|---|
| Large Rectangle | 100 sq units | 50 sq units |
| Small Square | 25 sq units | |
| Intersection of Circles | 75 sq units |

🧩 Note: Sometimes, the shaded region can be a composite shape where parts are added or subtracted.
Tip #3: Master the Formulae

Knowing the area formulas for common shapes is crucial. Here are some key formulae:
- Circle: A = \pi r^2
- Rectangle: A = l \times w
- Triangle: A = \frac{1}{2} \times b \times h
Additionally, for more complex shapes:
- Integrate or use calculus for irregular areas under curves.
- Employ techniques like transformation of coordinates for symmetrical shapes.
Tip #4: Use Symmetry and Properties

Symmetry can significantly simplify your calculations:
- Reflect the shape to visualize how symmetry can help.
- Use the centroid or center of mass to find the middle point.
- Check if any properties (like area moments) can be used to simplify your problem.
Symmetry can help you reduce complex problems to simpler components:
- Divide the shaded area by lines of symmetry to work on smaller, manageable pieces.
Tip #5: Practice with Real-world Problems
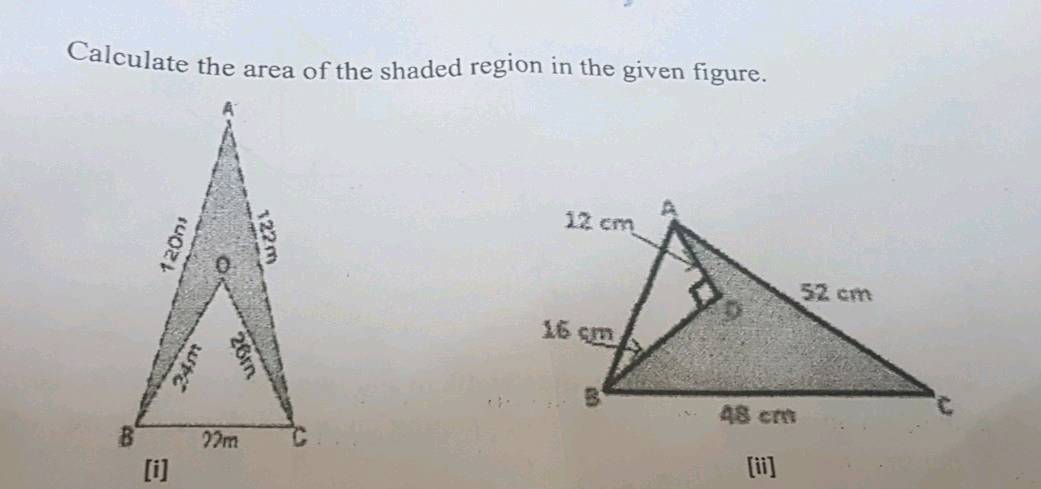
The best way to master shaded region calculations is through practice:
- Work on problems from textbooks or online resources.
- Engage in real-world design tasks like garden layouts or plot divisions.
- Try problems from engineering, where precise area calculations are often required.
The real-world applications ensure you understand the practical implications of geometric calculations:
- Designing furniture layouts.
- Calculating the amount of paint needed for complex room shapes.
- Optimizing space in land development.
In closing, these tips provide a comprehensive framework for tackling shaded region calculations. From visualizing and understanding the geometry to mastering the required mathematical tools, each step is crucial in simplifying what might otherwise appear as a complex task. By consistently practicing these methods, you'll develop a keen eye for problem-solving in geometry, making the task of calculating shaded regions more approachable and manageable.
What if the shaded region is made up of very complex shapes?

+
If dealing with highly complex shapes, consider using software or tools like CAD for precise calculations. Sometimes, it’s also beneficial to break down the problem into more familiar shapes and use numerical integration for irregular areas.
How can I verify if my area calculation is correct?

+
One way is by using alternative methods like counting squares on graph paper, using software for validation, or double-checking with different techniques like Simpson’s rule or Trapezoidal rule for numerical integration.
Are there any tricks for calculating the area of irregular shapes?

+
For irregular shapes, you might employ Monte Carlo simulations to estimate areas by randomly sampling points within a bounding shape. Also, techniques like numerical integration or grid approximation can be very useful.