5 Ways to Master Regular Polygon Area Calculation

If you've ever needed to calculate the area of shapes in your daily life or as part of your studies, understanding how to master the area calculation of regular polygons can be extremely useful. Regular polygons, by definition, have all sides and angles equal, making certain formulas straightforward to apply. Here's how you can become an expert in this:
1. Understanding the Basics of Regular Polygons

Before you dive into the calculations, it’s important to grasp what a regular polygon is:
- Equal sides
- Equal angles
- Inscribed in or circumscribing a circle
Each of these characteristics simplifies the calculation because the regularity allows us to use simple mathematical expressions. For example, in a regular polygon, each internal angle can be calculated using the formula:
[ \text{Interior Angle} = \frac{(n - 2) \times 180}{n} ]
📐 Note: Here, 'n' represents the number of sides of the polygon.
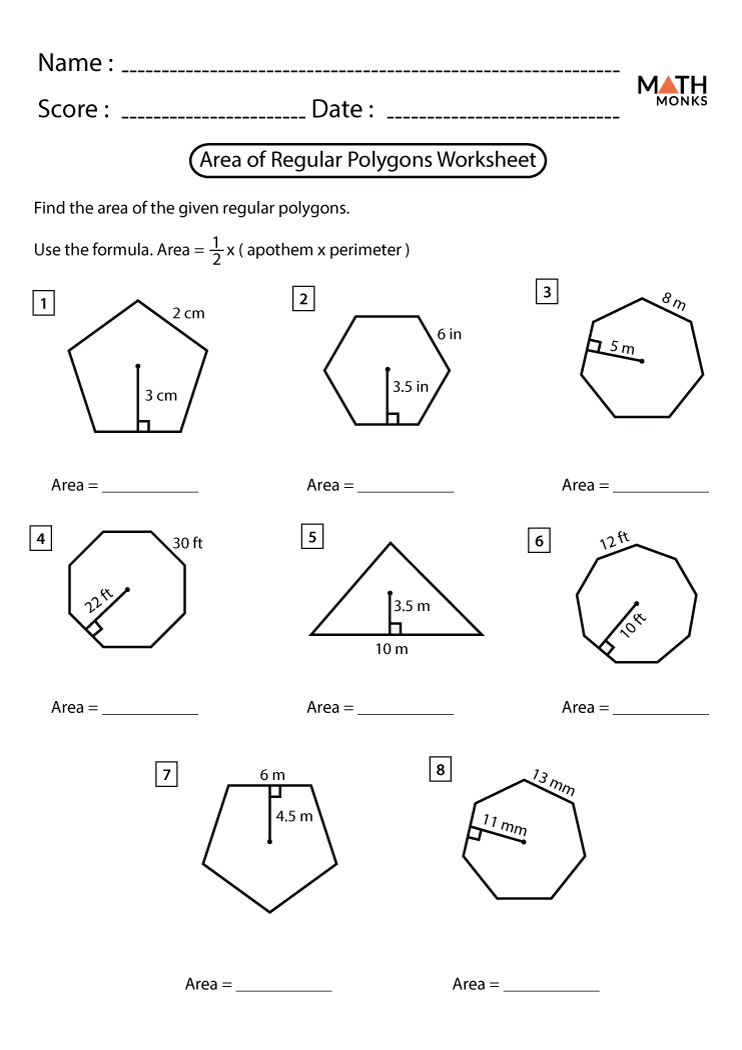
2. Using the Apothem for Area Calculation

The apothem of a regular polygon is the line segment from the center to the midpoint of any side. The formula for calculating the area is:
[ \text{Area} = \frac{1}{2} \times n \times s \times a ]
where:
- n is the number of sides
- s is the side length
- a is the apothem
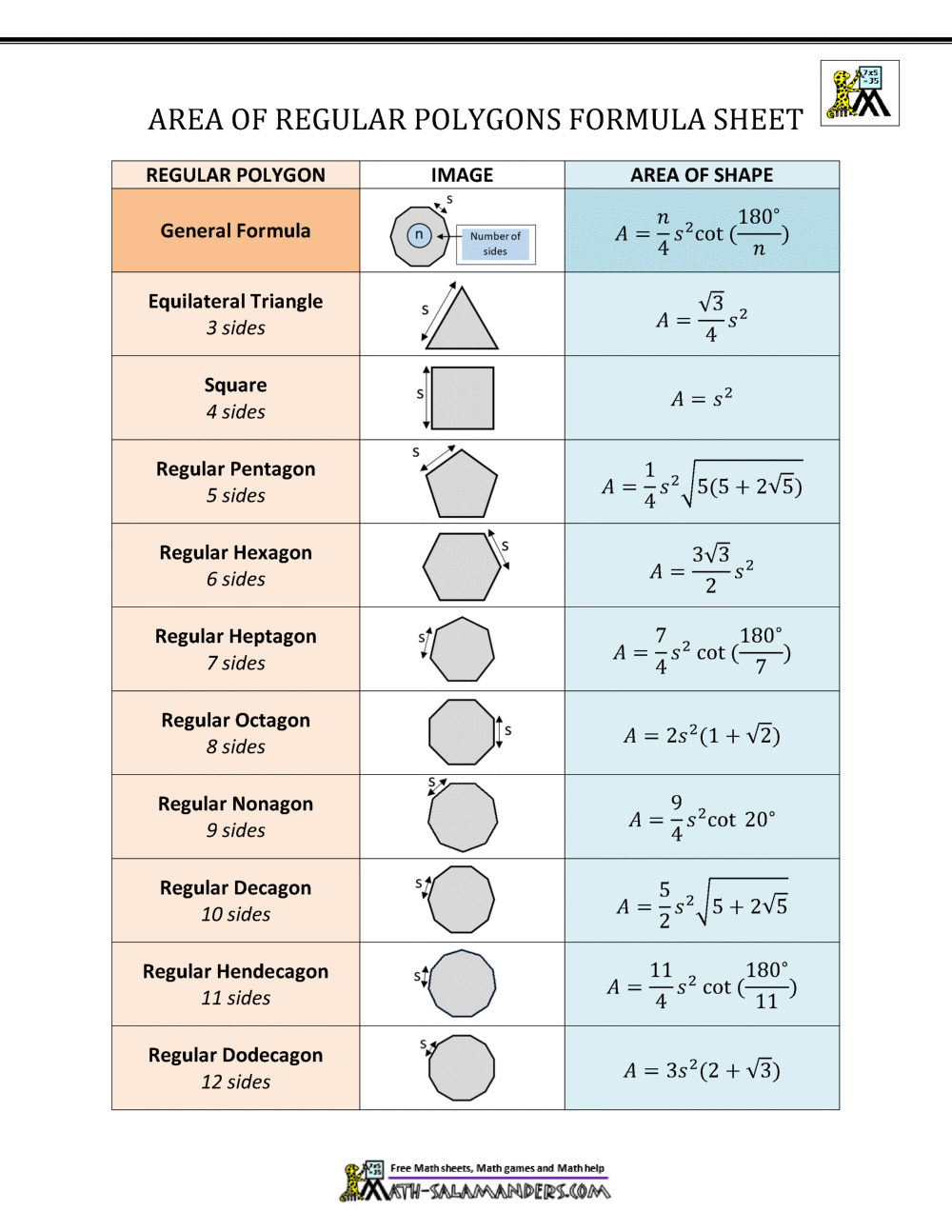
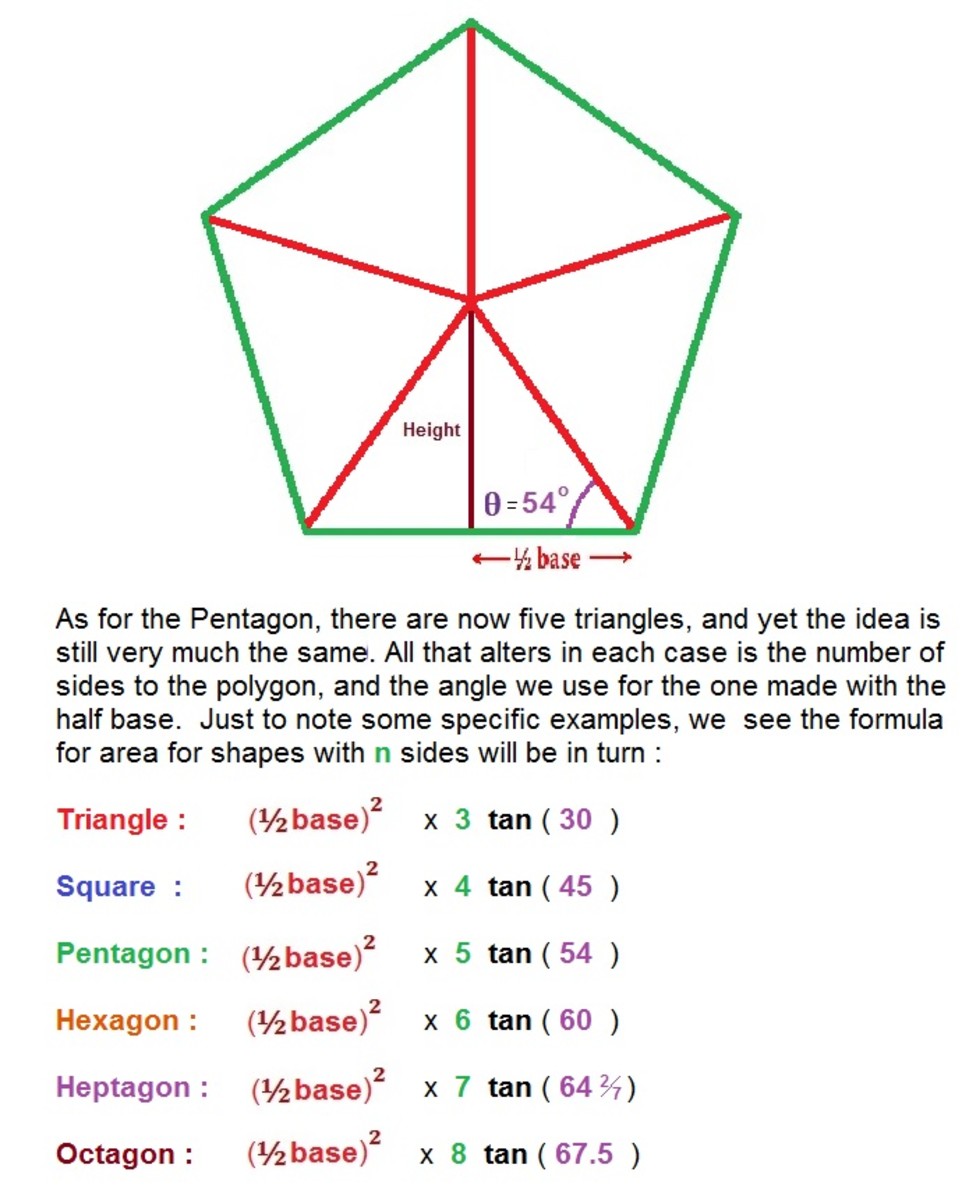
3. Direct Side-Length Approach
You can also calculate the area directly from the side length using:
[ \text{Area} = \frac{n \times s^2}{4 \times \tan(\pi/n)} ]
🔍 Note: This formula becomes more accurate as the number of sides increases, approaching the area calculation for a circle.
4. Practicing with Real-World Examples
To truly master the calculation, practice is key:
- Measure and calculate the area of common household objects that can approximate regular polygons.
- Work through mathematical word problems or real-world scenarios involving polygons.
5. Leveraging Technology and Software
While the formulas are essential, modern tools can help:
- Use geometric software to visualize and manipulate polygons, observing how changes affect the area.
- Online calculators can verify your hand calculations or help with more complex polygons.
💻 Note: Technology should complement, not replace, your understanding of the underlying math.
Summing up, becoming proficient in calculating the area of regular polygons involves understanding the basic properties, applying various formulas, and engaging with both manual and technological methods. With practice, you'll find yourself not just calculating areas but also appreciating the beauty of symmetry and geometry in everyday shapes. This knowledge not only enhances your mathematical abilities but also helps in practical applications like architecture, design, and beyond.
Can I use these formulas for any polygon?

+
These formulas are specifically for regular polygons. For irregular polygons, you might need to divide them into simpler shapes or use more complex calculus.
What if I only know the radius of the circumscribed circle?

+
With the radius ® of the circumscribed circle, you can find the area using the formula: Area = (\frac{n \times R^2}{2} \times \sin\left(\frac{2\pi}{n}\right) ).
Do these calculations change for non-convex polygons?

+
For non-convex polygons, the formulas remain the same for the area calculation, but the interpretation of angles and sides might differ as the shape can fold back on itself.



