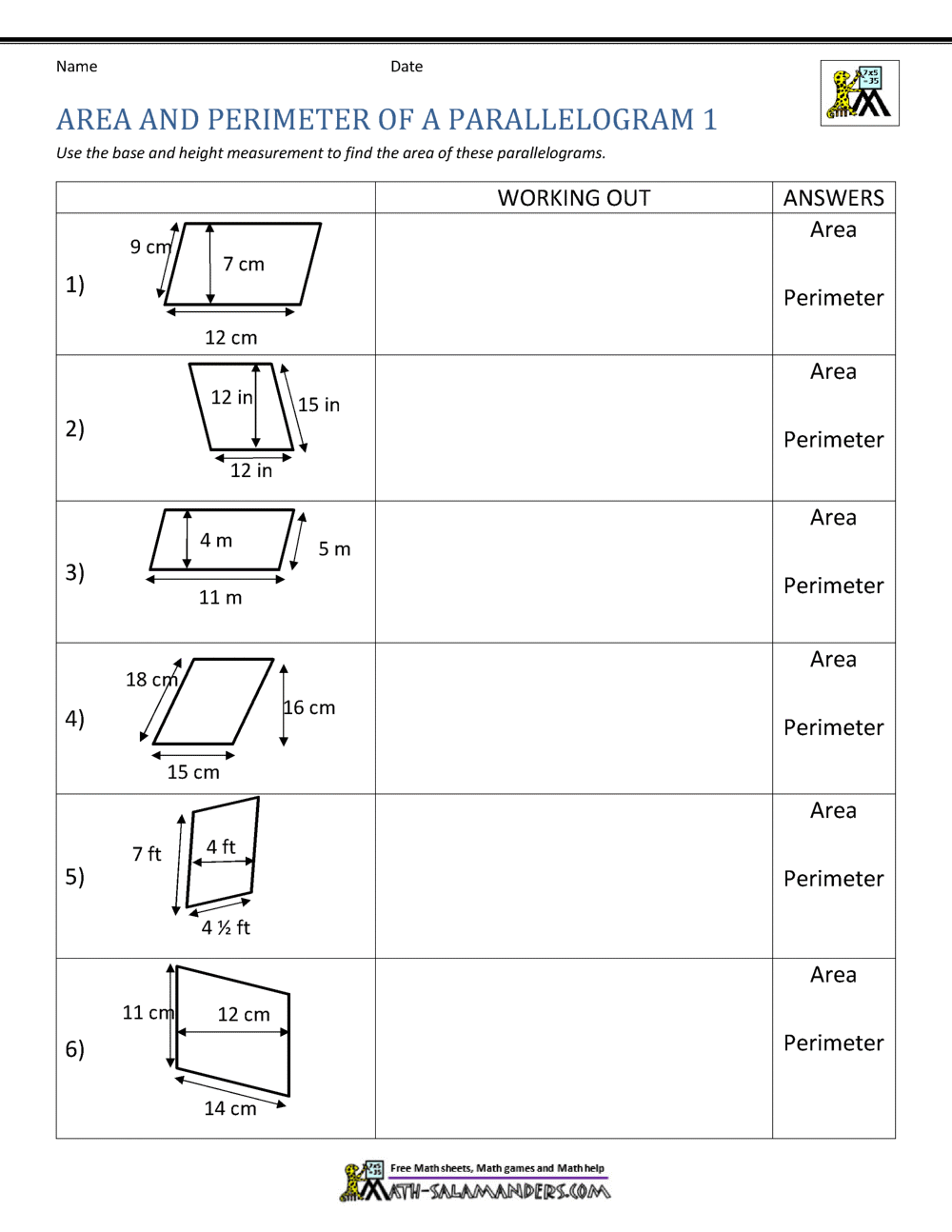
Area of Parallelograms Worksheet: Quick and Easy Math Practice

The understanding of geometric shapes and their properties plays a critical role in mathematics education, with the parallelogram being a classic example frequently examined due to its distinct characteristics. For students, educators, and math enthusiasts looking to deepen their grasp on parallelograms, this blog post provides a comprehensive area of parallelograms worksheet along with guidelines on how to approach these problems effectively. Whether you're a student preparing for an upcoming math exam, a teacher looking to refine your lesson plan, or someone simply interested in exploring mathematical principles, this post will guide you through the steps to master calculating the area of parallelograms.
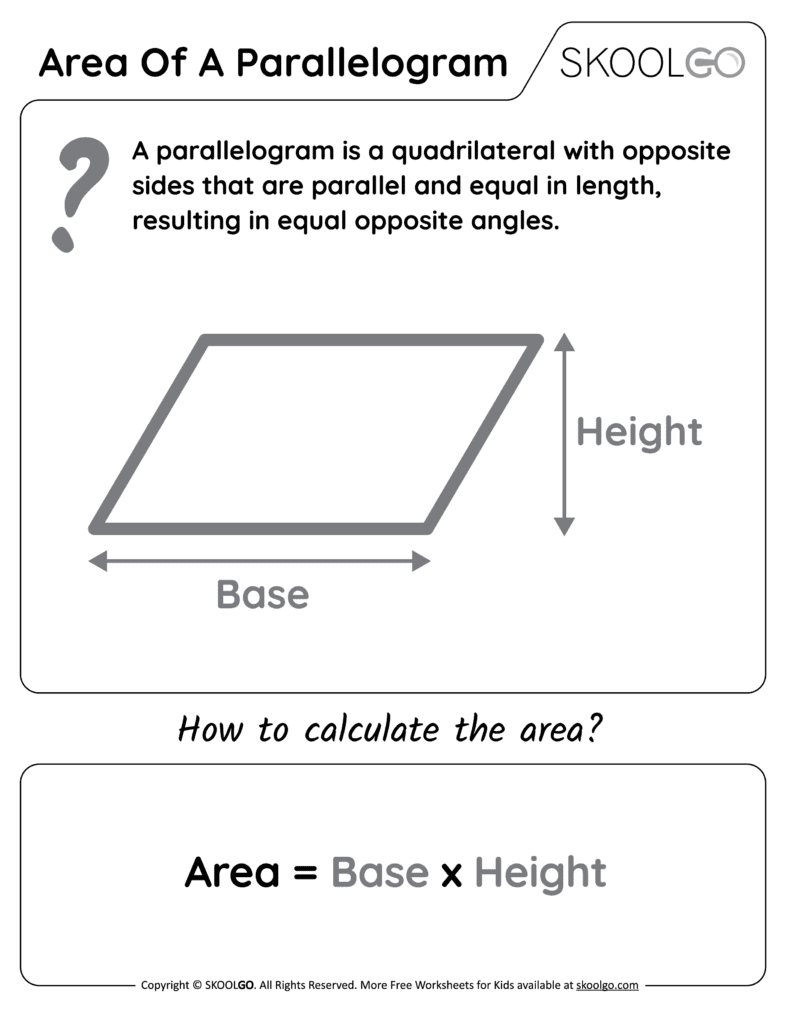
The Basics of Parallelograms
A parallelogram is a quadrilateral characterized by two pairs of parallel sides. This unique feature leads to several properties, which are fundamental when solving related problems:
- Opposite sides are equal in length.
- Opposite angles are equal.
- The sum of consecutive angles equals 180 degrees.
- Diagonals bisect each other.
Understanding these characteristics is crucial before diving into area calculations.
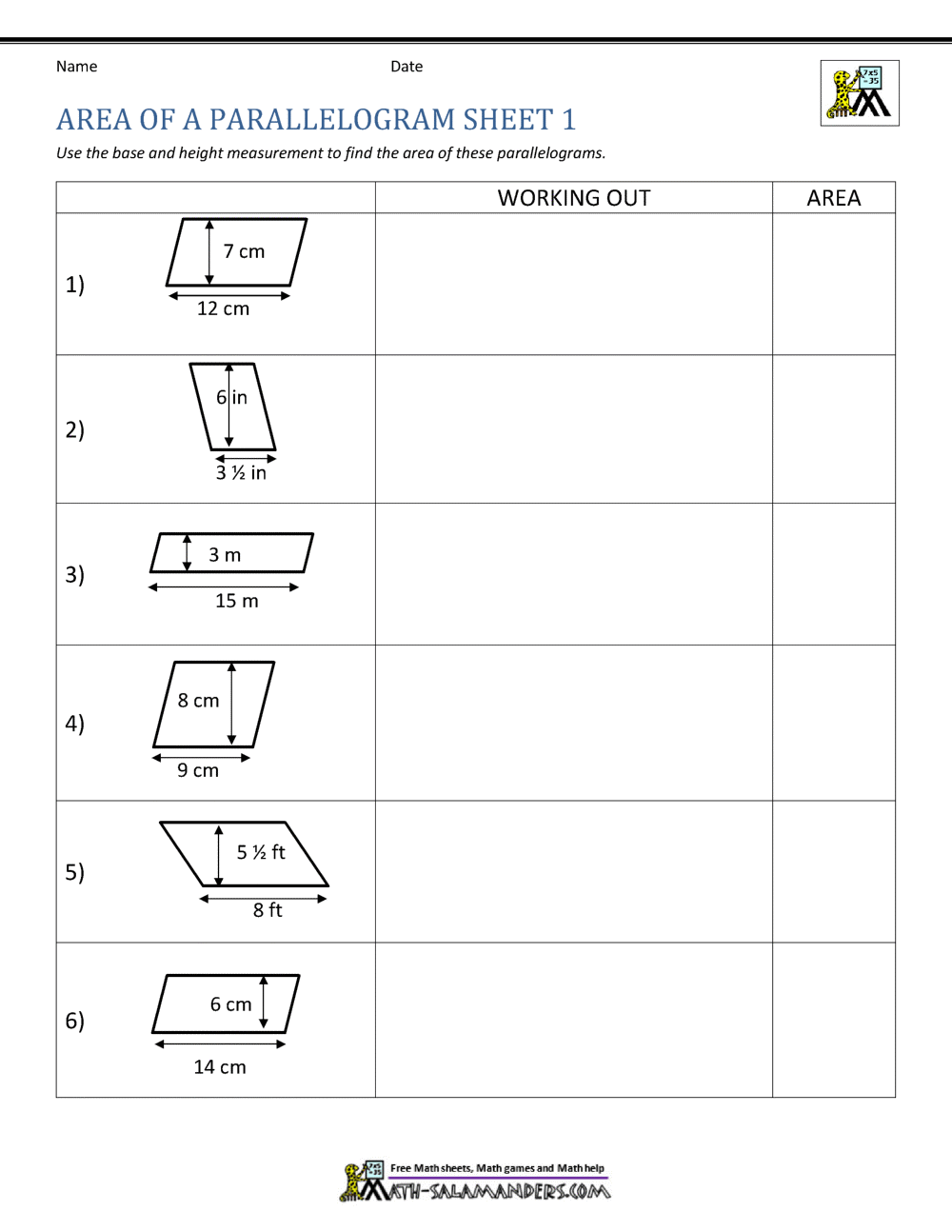
Formula for the Area of a Parallelogram

The area A of a parallelogram can be calculated using the formula:
A = b × h
Where b is the base length and h is the height, which is the perpendicular distance between the parallel sides.
Area of Parallelograms Worksheet

Let's walk through a step-by-step process to solve parallelogram area problems:
1. Identifying the Base and Height
To calculate the area, you first need to identify the base and the height:
- Base: Any side of the parallelogram.
- Height: The perpendicular distance from the base to the opposite side. Ensure you're not using the slant height, as this will give an incorrect result.
Example: Calculate the area of a parallelogram with a base of 5 cm and a height of 3 cm.
A = 5 cm × 3 cm = 15 cm²
📐 Note: When sketching, always label the base and height clearly.
2. Using Known Properties
If you're not given the height, you can use parallelogram properties to find it:
- If you know one angle and one side, you can find the height using trigonometry: h = b * sin(θ), where θ is the angle between the side and the base.
3. Real-Life Application
Parallelograms can model real-life objects. For instance, consider a garden plot shaped like a parallelogram:
| Base (m) | Height (m) | Area (m²) |
|---|---|---|
| 12 | 8 | 96 |
| 15 | 6 | 90 |
| 10 | 7 | 70 |
🌱 Note: Understanding the geometry of garden plots helps in planning planting areas efficiently.
Conclusion

Mastering the area of parallelograms involves understanding its basic properties, accurately identifying the base and height, and applying the area formula or using known properties when direct measurements are unavailable. The exercises provided in this blog aim to reinforce these concepts through practical application, ensuring that you can apply these skills in various contexts, from simple worksheets to real-life scenarios. Remember, the key to success in mathematics lies in consistent practice and a solid understanding of the fundamentals.
Why do we need to calculate the area of parallelograms?
+
Calculating the area helps in understanding and measuring the space occupied by an object, which is crucial in fields like land surveying, architecture, and engineering.
What if I only know one side and one angle of the parallelogram?

+
You can use the trigonometric relationship to find the height: h = b * sin(θ), where b is the known side and θ is the angle between the side and the base.
Can I calculate the area if I have the lengths of all four sides but not the height?
+
Yes, you can use the formula A = sqrt((2*b₁*b₂)*cos(θ)), where b₁ and b₂ are the lengths of two adjacent sides and θ is the angle between them.
How can I verify my area calculations?

+
You can check your work by applying another method or using known relationships between the sides and angles of the parallelogram, or by constructing the parallelogram in a geometric software to measure its area directly.