6 Simple Ways to Calculate Triangle Area

Calculating the area of a triangle is a fundamental skill in geometry that has applications in various fields such as architecture, engineering, and surveying. Whether you're a student learning the basics or a professional working on real-world problems, understanding how to find the area of a triangle can be incredibly useful. Here are six straightforward methods to calculate the area of a triangle, each suited to different scenarios:
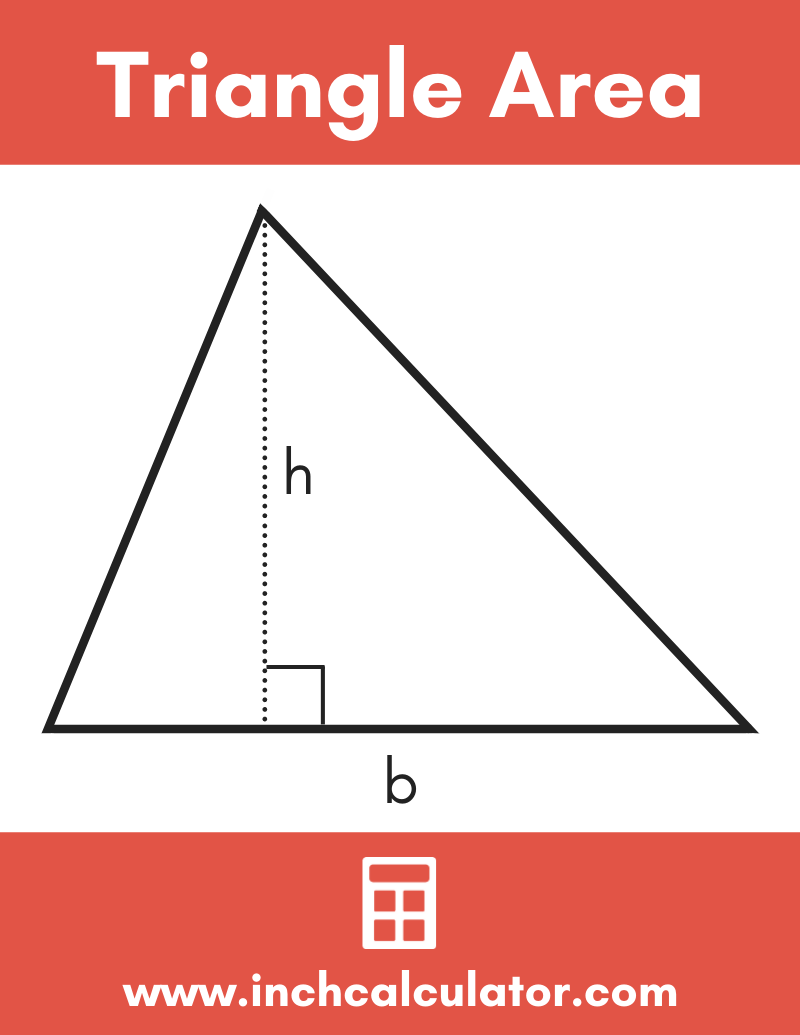
1. Base and Height Method

This is the most commonly taught method in school geometry. The area A of a triangle can be calculated with the following formula:
- Identify the base: This is usually the side of the triangle that is considered at the bottom when the triangle is drawn.
- Determine the height: This is the perpendicular distance from the base to the opposite vertex.
- Calculate: Multiply the base by the height and divide by two.
📏 Note: The base and height must be perpendicular to each other for this formula to work correctly.
2. Heron’s Formula

Heron’s formula is used when you only know the lengths of the three sides of the triangle:
- s is the semi-perimeter of the triangle:
s = \frac{a + b + c}{2} - a, b, and c are the lengths of the sides.
Here’s how you use it:
- Sum up the sides to find the semi-perimeter s.
- Plug the values into Heron’s formula and compute the square root.
3. Trigonometry

If you know two sides of the triangle and the angle between them, you can use trigonometry to find the area:
- a and b are the sides adjacent to the angle C.
- C is the included angle between the sides.
4. Using Coordinates

For triangles defined by their vertices in a coordinate system, the area can be calculated using the determinant method:
- Let the coordinates of vertices A, B, and C be (x1, y1), (x2, y2), and (x3, y3) respectively.
- Substitute these coordinates into the formula to find the absolute value.
📌 Note: This method assumes the vertices are listed in order, either clockwise or counterclockwise.
5. For Right-Angled Triangles
If the triangle has a right angle, calculating its area becomes much simpler:
- The two legs form a right angle, and their product divided by 2 gives the area.
6. Using the Inradius and Semi-Perimeter

The area of a triangle can also be found knowing its inradius r (the radius of the inscribed circle) and its semi-perimeter s:
To summarize, the area of a triangle can be found through various methods, each with its unique prerequisites:
- The base and height method is straightforward and widely used when you have access to the triangle’s geometry.
- Heron’s formula allows calculation when only side lengths are known, making it particularly useful for irregular triangles.
- Using trigonometry is beneficial when dealing with angles or when triangles are not directly measurable in terms of height or base.
- Coordinate geometry simplifies the process when dealing with triangles in a spatial context, often encountered in programming or engineering applications.
- For right-angled triangles, the calculation is as simple as multiplying the legs.
- Inradius and semi-perimeter approach provides an elegant solution when internal measurements are known.
These methods ensure that no matter the information available or the specific type of triangle you’re dealing with, you can always find its area efficiently.
By mastering these techniques, you’ll have a solid foundation for tackling geometric problems and applying these principles in real-life situations or further advanced mathematical studies.
What if my triangle is not right-angled?

+
For non-right-angled triangles, you can use Heron’s formula, trigonometry, or the determinant method using coordinates.
How accurate are these methods?

+
The accuracy depends on the precision of your measurements and calculations. With exact or highly precise measurements, these methods can yield very accurate results.
Can these methods be used for any shape of triangle?

+
Yes, these methods are universally applicable to any triangle, whether it’s acute, obtuse, right, equilateral, isosceles, or scalene.



