5 Tips to Master Area of Compound Shapes

Understanding Compound Shapes

Compound shapes, sometimes known as composite figures, are a combination of simple geometric shapes like rectangles, triangles, circles, and more complex polygons. Mastering how to calculate the area of compound shapes is crucial, not only in mathematics but also in applications like construction, graphic design, and urban planning. Here are five effective tips to help you master the area of compound shapes:
1. Break Down the Shape

The first step in tackling the area of compound shapes is to visually or mentally break down the figure into recognizable basic shapes. Here’s how:
- Identify Basic Shapes: Look at the compound shape and isolate all the simple shapes within it. Common shapes include rectangles, squares, triangles, circles, and trapezoids.
- Separate and Label: Clearly delineate and label each part so you don’t confuse one section with another during your calculations.
⚠️ Note: When dealing with curved edges, approximate circles or circular sectors might be involved, which require different calculation methods.
2. Use Familiar Formulas
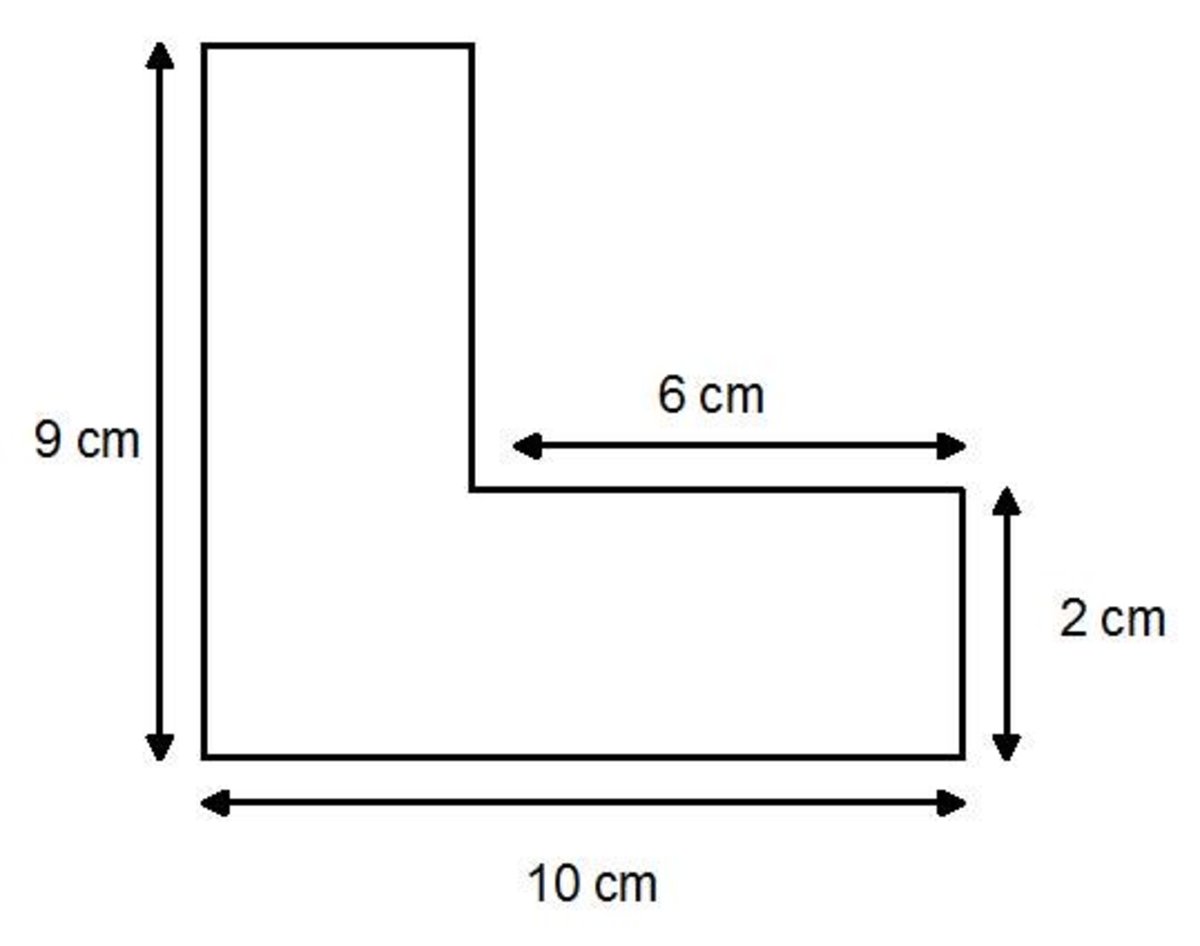
Once you’ve separated your compound shape, use the following formulas for the respective basic shapes:
| Shape | Formula |
|---|---|
| Rectangle | Area = Length × Width |
| Square | Area = Side × Side |
| Triangle | Area = ½ Base × Height |
| Circle | Area = π × Radius2 |
| Parallelogram | Area = Base × Height |
| Trapezoid | Area = ½ (Base1 + Base2) × Height |

Applying these formulas to the respective subshapes of your compound figure is fundamental.
3. Calculate Each Part

With the formulas at your fingertips, proceed to calculate the area of each subshape:
- Measure Accurately: Ensure the measurements of length, width, or any other dimensions are taken correctly.
- Perform Calculations: Use a calculator if needed, especially for complex numbers or irrational constants like π.
4. Add or Subtract

The area of the compound shape is usually found by adding or subtracting the areas of the subshapes:
- Addition: If parts of the shapes overlap or are part of a larger whole, add their areas.
- Subtraction: Sometimes, a part might need to be subtracted, like a hole within a larger shape.
✅ Note: Be careful with signs—subtraction means you are taking away area, while addition means you're combining areas.
5. Use Geometrical Properties
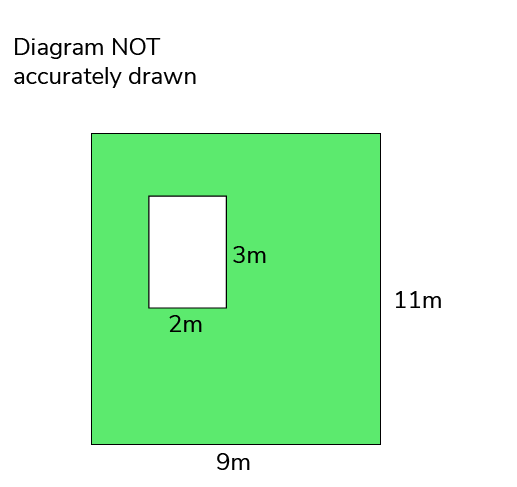
Understanding and using geometric properties like symmetry, congruent shapes, or similarity can simplify your work:
- Symmetry: If a shape is symmetrical, you can calculate half and multiply by two.
- Similar Figures: Similar shapes have proportional areas based on their linear dimensions.
- Congruence**: Congruent shapes have equal areas.
In mastering these tips, you’ll notice that the calculation of compound shapes isn’t just about math; it’s about problem-solving, visualization, and applying learned formulas. Whether you’re a student grappling with a geometry problem or a professional dealing with real-world applications, these strategies can streamline your approach to complex shapes.
These steps provide a structured method to unravel the complexity of compound shapes. With practice, you’ll become adept at identifying, measuring, and calculating the area of various composite figures with ease and accuracy.
What if the compound shape includes irregular shapes?

+
For shapes with irregular boundaries, you might approximate using basic shapes or use methods like integration or grid approximation.
How do I handle very complex shapes with many sub-shapes?

+
Complex shapes can often be broken down into simpler, overlapping or touching shapes. Carefully work through each part systematically.
Can I use software to calculate areas of compound shapes?

+
Yes, various CAD, GIS, and mathematical software can compute areas efficiently, especially when dealing with shapes that have curved or complex boundaries.



