Mastering Rectangle Math: Area and Perimeter Worksheet

Exploring Rectangle Geometry
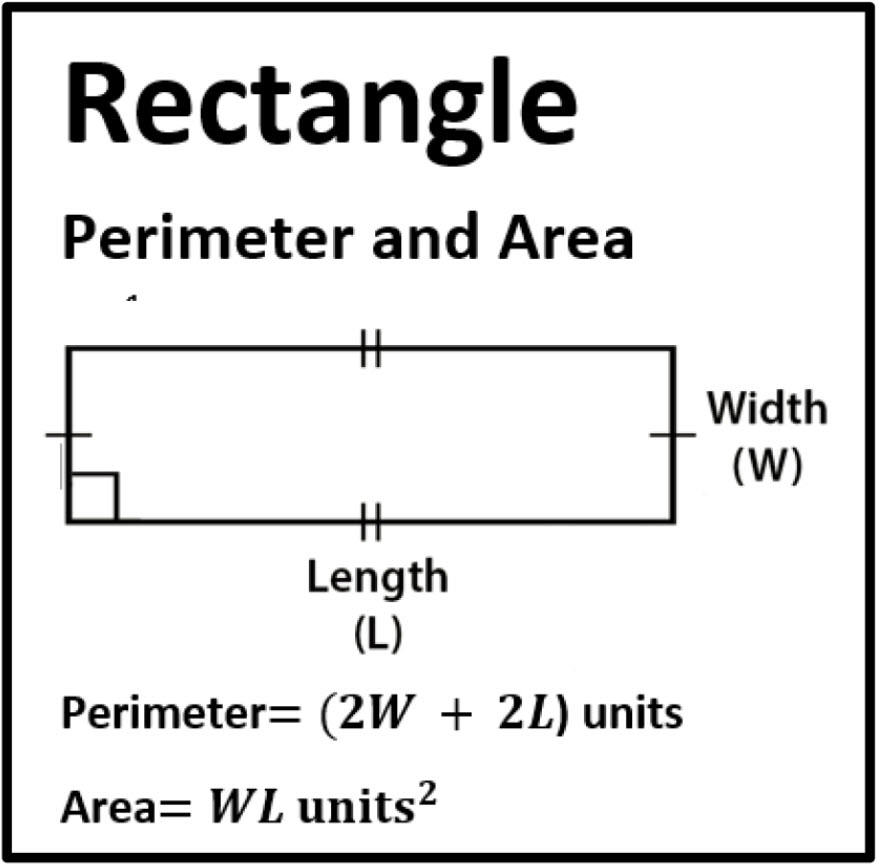
A rectangle, with its four right angles and parallel sides, embodies simplicity and symmetry, making it one of the most fundamental shapes in geometry. In this comprehensive guide, we will delve into the basics of rectangle geometry, focusing on the calculation of its area and perimeter. Understanding these concepts not only strengthens your foundational knowledge but also aids in solving a wide range of mathematical problems and real-world applications.
Understanding the Basics

Before we jump into the calculations, let’s define the key terms:
- Length (L): The longer side of the rectangle.
- Width (W): The shorter side of the rectangle.
- Area: The total amount of space inside the rectangle, measured in square units.
- Perimeter: The total distance around the rectangle’s boundary, measured in linear units.
Calculating Area

The formula for the area of a rectangle is straightforward:
🔍 Note: Area = Length × Width
Here's how you can apply it:
- Identify the length and width of your rectangle.
- Multiply these two dimensions to find the area.
Calculating Perimeter

The perimeter of a rectangle can be calculated with the following formula:
🔍 Note: Perimeter = 2 × (Length + Width)
The steps to follow are:
- Sum the length and width.
- Multiply the result by 2 to get the perimeter.
Practical Examples

To cement your understanding, let’s work through a couple of practical examples:
Example 1: Calculating Area
Consider a rectangle with a length of 12 units and a width of 5 units. Here’s how you would find the area:
- Area = 12 units × 5 units = 60 square units
Example 2: Calculating Perimeter
For the same rectangle, we now calculate the perimeter:
- Perimeter = 2 × (12 units + 5 units) = 34 units
Using Visuals

Visual aids can significantly enhance understanding, especially in geometry. Below is a table summarizing different rectangles with their respective lengths, widths, areas, and perimeters:
| Rectangle No. | Length (L) | Width (W) | Area | Perimeter |
|---|---|---|---|---|
| 1 | 8 units | 3 units | 24 square units | 22 units |
| 2 | 10 units | 6 units | 60 square units | 32 units |
| 3 | 15 units | 9 units | 135 square units | 48 units |

Notes

🔍 Note: When calculating perimeter, the units remain linear, unlike area which results in square units. Be mindful of this when presenting or interpreting your results.
Mastering the calculation of area and perimeter for rectangles is not just about numbers; it's about understanding spatial relationships, enhancing visual literacy, and applying these skills to various contexts from home design to packaging solutions. By grasping these fundamental geometric principles, you open doors to a better understanding of more complex shapes and measurements.
Why is the rectangle considered a basic shape in geometry?

+
Rectangles are fundamental because of their symmetry and the ease with which they can be divided into squares or cut diagonally into right triangles, making them versatile for understanding area and volume calculations.
How does learning to calculate area and perimeter benefit real-life scenarios?

+
From designing rooms and landscapes to optimizing material use in manufacturing, understanding rectangle dimensions helps in planning and resource management, saving both time and money.
Can the formulas for area and perimeter be applied to other shapes?

+
Yes, with modifications. For example, the perimeter formula can be adapted to find the perimeter of shapes like squares or parallelograms, while the area formula has variations for triangles and circles.



