Arcs, Semicircles, and Central Angles Worksheet Answers Revealed

Mathematics often presents us with problems that require the understanding and application of geometric properties. Among these are circles, semicircles, and the arcs they create, which along with central angles, become the foundation for many geometric challenges. This blog post dives deep into the mysteries of arcs, semicircles, and central angles, providing a comprehensive worksheet answers guide to help learners grasp these concepts with ease.
Understanding Arcs and Circles
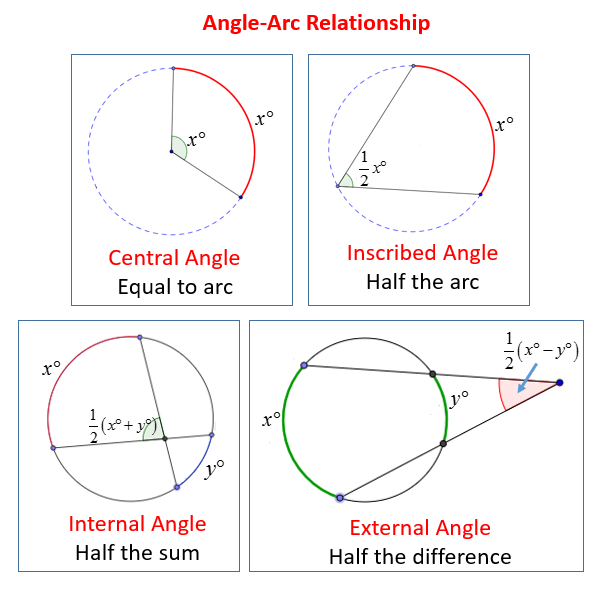
The core of our discussion begins with the circle, defined as the locus of all points equidistant from a fixed point known as the center. Let’s explore:
- Arc: A portion of the circumference of a circle.
- Chord: A straight line segment with endpoints on the circle.
- Central Angle: An angle formed by two radii at the center of the circle.
💡 Note: Remember, the circumference of a circle is calculated by the formula C = 2\pi r, where r is the radius.
Calculating Arcs and Semicircles

When we dive into calculating arcs and semicircles, here’s how we can approach it:
1. Arc Length

To calculate the length of an arc in a circle, we use:
- Arc Length Formula: (L = r \theta) where (L) is the arc length, (r) is the radius, and (\theta) is the angle in radians.
2. Semicircle Calculations

A semicircle is half a circle:
- Length of Semicircle: ( \frac{\pi r}{2} ).
- Area of Semicircle: ( \frac{1}{2} \pi r^2 ).
📝 Note: The angle of a semicircle, when measured from the center, is always 180^\circ or \pi radians.
Solving Worksheet Problems

Let’s tackle some common worksheet problems involving arcs, semicircles, and central angles:
Problem 1: Finding Arc Length
Given a circle with a radius of 5 units and a central angle of (60^\circ):
- Step 1: Convert (60^\circ) to radians (( \theta = \frac{60 \times \pi}{180} \approx 1.047 ) radians).
- Step 2: Apply the formula for arc length ((L = r\theta = 5 \times 1.047 \approx 5.235) units).
Problem 2: Area of a Semicircle

If the diameter of a circle is 12 units, find the area of its semicircle:
- Step 1: Calculate the radius ((r = \frac{12}{2} = 6) units).
- Step 2: Use the semicircle area formula ((A = \frac{1}{2} \pi r^2 = \frac{1}{2} \times \pi \times 6^2 = 18\pi) square units).
Problem 3: Central Angle and Arc Length

A circle with a radius of 4 units has an arc length of 6 units. Find the central angle:
- Step 1: Use the arc length formula to find (\theta) ((6 = 4 \times \theta \rightarrow \theta = \frac{6}{4} = 1.5) radians).
- Step 2: Convert the angle to degrees ((1.5 \times \frac{180}{\pi} \approx 85.94^\circ)).
In this comprehensive guide, we've unveiled the intricacies of arcs, semicircles, and central angles, providing detailed answers to worksheet problems. Understanding these concepts will not only enhance your problem-solving skills in geometry but also prepare you for more complex mathematical problems involving circles and curves. Each step builds on the previous knowledge, highlighting how foundational geometry can be expanded into practical, real-world applications. From calculating the length of an arc to finding the area of a semicircle, we've laid out the steps to master these mathematical challenges.
Why are arc lengths and central angles important?
+
Understanding arc lengths and central angles helps in various real-world applications like engineering, architecture, and even in daily navigation systems.
Can the arc length ever be longer than the diameter?

+
No, the longest arc you can have is the semicircle itself, which equals the diameter in length.
How do you calculate the angle of a minor arc?

+
The angle of a minor arc is simply the central angle in degrees or radians that corresponds to the arc segment shorter than the semicircle.