Arc Length and Sector Area: Worksheet With Answers

If you're interested in diving deeper into the intriguing world of geometry, focusing specifically on arc length and sector area, then this article is for you. Geometry isn't just about understanding shapes and sizes; it's about solving practical problems in fields ranging from engineering to design. Here, we'll walk through the foundational concepts, provide you with tools to calculate these measurements, and share some practice problems to sharpen your skills.
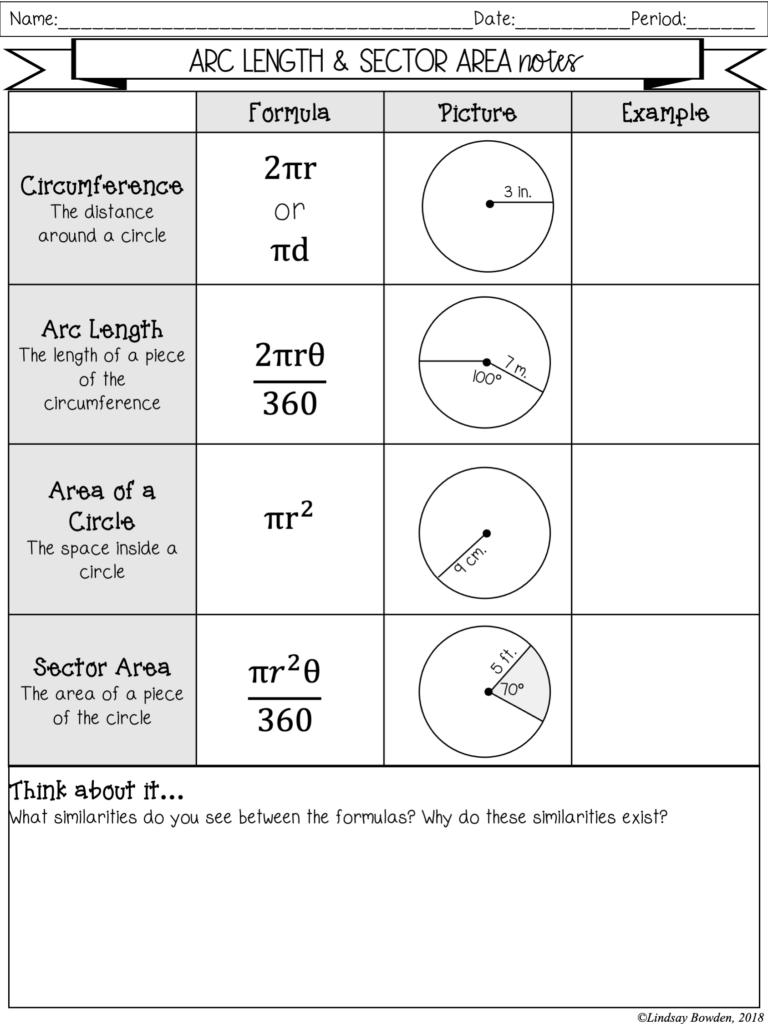
Understanding Arc Length

The arc length of a circle, or arc for short, is the distance along the circumference (edge) of a circle or any other curved line. Calculating it can seem daunting at first, but the formula simplifies it significantly:
- Arc Length Formula: (L = \theta \times r), where (L) is the arc length, (\theta) is the angle in radians, and (r) is the radius of the circle.
Here’s how to calculate it:
- Convert the angle from degrees to radians if necessary. Remember, (180° = \pi) radians.
- Multiply the angle (in radians) by the radius of the circle.
Let’s illustrate with an example:
| Angle | Radius | Arc Length |
|---|---|---|
| 60° (or (\frac{\pi}{3}) radians) | 5 units | (\frac{\pi}{3} \times 5 \approx 5.24) units |

Calculating Sector Area

The sector of a circle is a fraction of the circle’s area formed between two radii and an arc. The formula for the sector area is:
- Sector Area Formula: (A = \frac{1}{2} \times \theta \times r^2), where (A) is the sector area, (\theta) is the angle in radians, and (r) is the radius.
Similar to arc length, you might need to:
- Convert the angle to radians if it’s given in degrees.
- Apply the formula using the given or calculated angle in radians.
Example calculation:
| Angle | Radius | Sector Area |
|---|---|---|
| 60° (or (\frac{\pi}{3}) radians) | 5 units | (\frac{1}{2} \times \frac{\pi}{3} \times 5^2 \approx 13.09) square units |
Practice Problems

Now that we’ve covered the theoretical aspects, let’s dive into some practical problems to solidify your understanding:
Problem 1: Arc Length

Find the arc length of a circle with radius 7 units and an angle of 54°.
Solution:
- Convert 54° to radians: (54 \times \frac{\pi}{180} = 0.9425) radians.
- Arc length = (0.9425 \times 7 = 6.5975 \approx 6.60) units.
Problem 2: Sector Area

Calculate the area of a sector in a circle where the angle is 36° and the radius is 10 units.
Solution:
- Convert 36° to radians: (36 \times \frac{\pi}{180} = 0.6283) radians.
- Sector area = (\frac{1}{2} \times 0.6283 \times 10^2 = 31.415 \approx 31.42) square units.
Applications in Real Life

Understanding arc length and sector area isn’t just academic; here are some applications:
- Architecture and Design: Curved elements like arches or circular rooms require precise measurements for materials and design.
- Land Surveying: Sectors can help in calculating land divisions or planning routes around curved natural features.
- Astronomy: Arc lengths are crucial in determining the apparent size of celestial bodies or distances between stars in a curved sky.
🌟 Note: Always ensure your calculator is set to radians mode when using trigonometric functions for these calculations.
Final Thoughts
Geometry offers a lens through which we can understand and interact with the physical world more intimately. By mastering concepts like arc length and sector area, you’re not only equipping yourself with mathematical knowledge but also with the ability to apply these principles to solve real-world problems. Keep practicing, and these calculations will become second nature, opening doors to various fields where geometry plays a pivotal role.
Why do we need to convert degrees to radians for these calculations?

+
The reason we convert degrees to radians is primarily for consistency with the mathematical formulas used in calculus. Radians provide a more natural measure of angles, where the angle is expressed in terms of arc length divided by the radius, which aligns with the definitions of arc length and sector area.
Can arc length ever be larger than the circumference of the circle?

+
No, the arc length can never be larger than the circumference of the circle. By definition, an arc is a part of the circumference, so its length must be less than or equal to the total circumference, which is (2\pi r).
How do I find the sector area without the angle in radians?

+
If you have the angle in degrees, you first convert it to radians. However, if you only know the arc length, you can use the formula for sector area indirectly by finding the angle using the arc length formula, then apply the sector area formula.