6 Ways to Master Arc Length and Sector Area Calculations
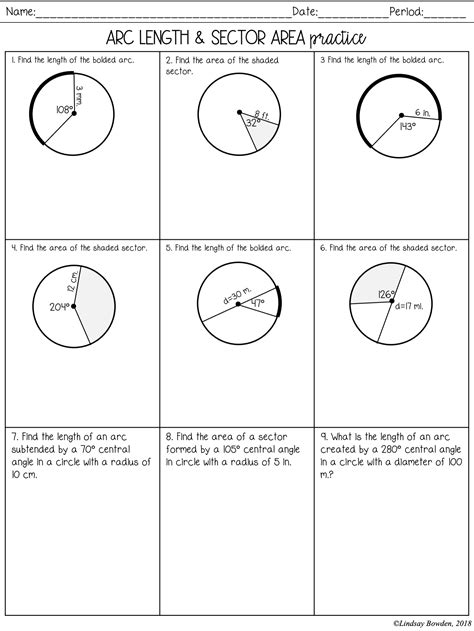
Understanding the Basics of Arc Length and Sector Area

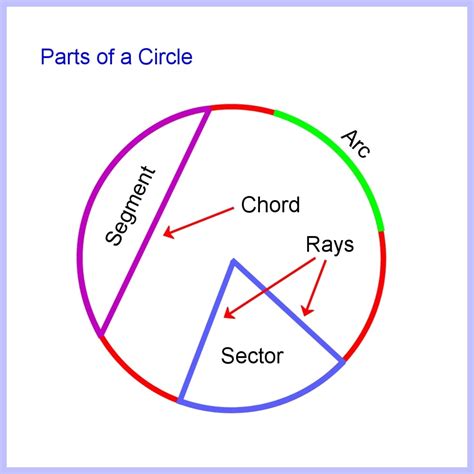
When dealing with circles and angles, two important concepts to master are arc length and sector area. Arc length refers to the distance along the circumference of a circle between two points, while sector area refers to the area enclosed by two radii and the arc between them. In this article, we will explore six ways to master arc length and sector area calculations.
1. Understanding the Formulas
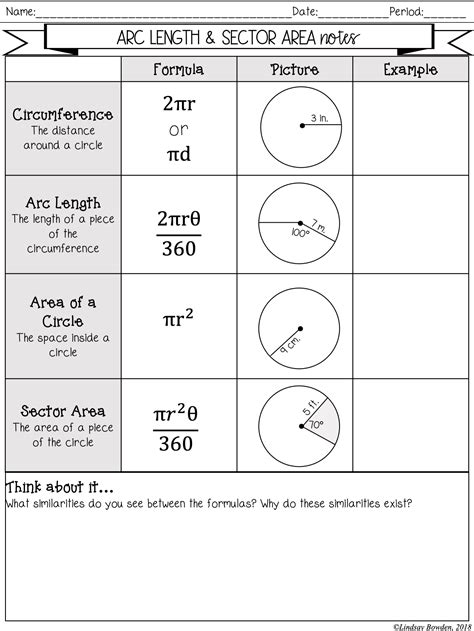
To start with, it’s essential to understand the formulas for calculating arc length and sector area.
- Arc Length (L) = (θ/360) × 2πr, where θ is the central angle in degrees, r is the radius of the circle, and π is a constant approximately equal to 3.14.
- Sector Area (A) = (θ/360) × πr^2
These formulas may seem straightforward, but it’s crucial to understand the variables and how they relate to each other.
2. Visualizing the Circle
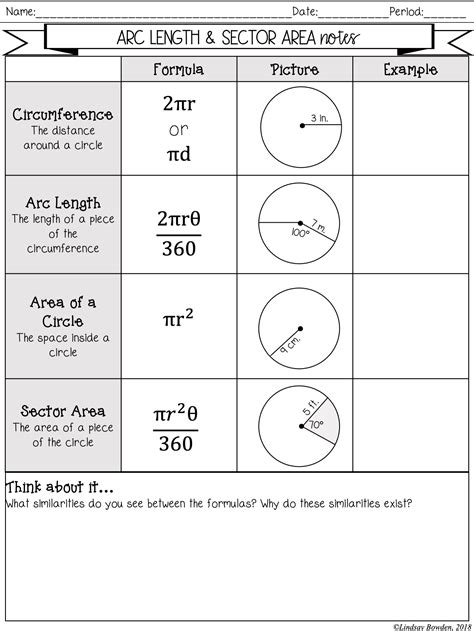
Visualizing the circle and the sector or arc in question can help you better understand the problem. Imagine a pizza with a slice missing – the missing slice represents the sector, and the length of the crust represents the arc length.

This visualization technique can help you identify the central angle, radius, and other essential components of the problem.
3. Breaking Down the Problem

When faced with a problem, break it down into smaller, manageable parts. Identify the given information, such as the central angle, radius, or arc length, and use this information to find the missing component.
For example, if you’re given the arc length and central angle, you can use the formula L = (θ/360) × 2πr to find the radius.
📝 Note: Always label the given information and the unknown variable to avoid confusion.
4. Using Real-World Applications

Arc length and sector area calculations have numerous real-world applications, such as:
- Architecture: designing circular arches, domes, or columns
- Engineering: calculating the area of a sector for a gear or pulley system
- Agriculture: determining the area of a circular field or irrigation system
Using real-world examples can help you understand the practical significance of these calculations and make the concepts more engaging.
5. Practicing with Different Units
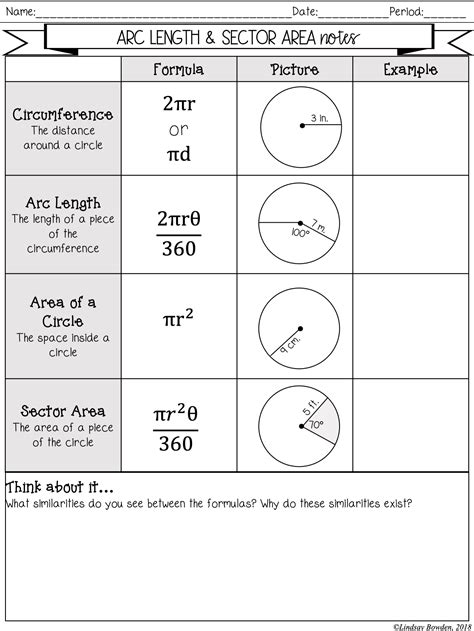
When practicing arc length and sector area calculations, try using different units, such as degrees and radians, or inches and centimeters. This will help you become more comfortable with conversions and ensure accuracy in your calculations.
| Unit | Conversion Factor |
|---|---|
| Degrees to Radians | π/180 |
| Inches to Centimeters | 2.54 |

6. Using Online Resources and Tools
There are numerous online resources and tools available to help you master arc length and sector area calculations. Some popular options include:
- Online calculators: websites that allow you to input values and calculate arc length and sector area
- Interactive simulations: interactive tools that allow you to visualize and experiment with different scenarios
- Video tutorials: video lessons that provide step-by-step instructions and explanations
These resources can supplement your learning and provide additional support when needed.
To summarize, mastering arc length and sector area calculations requires a combination of understanding the formulas, visualizing the circle, breaking down the problem, using real-world applications, practicing with different units, and utilizing online resources and tools. By following these six strategies, you’ll be well on your way to becoming proficient in these calculations.
What is the difference between arc length and sector area?
+
Arc length refers to the distance along the circumference of a circle between two points, while sector area refers to the area enclosed by two radii and the arc between them.
How do I convert between degrees and radians?
+
To convert from degrees to radians, multiply by π/180. To convert from radians to degrees, multiply by 180/π.
What are some real-world applications of arc length and sector area calculations?

+
Arc length and sector area calculations have numerous real-world applications, such as architecture, engineering, and agriculture.
Related Terms:
- area of sectors worksheet pdf
- circumference and arc length worksheet
- arc length worksheet pdf
- arc length and sectors worksheet
- trigonometry arc length problems
- arc length formula worksheet



