5 Tricks to Ace AP Physics Linearization Worksheet
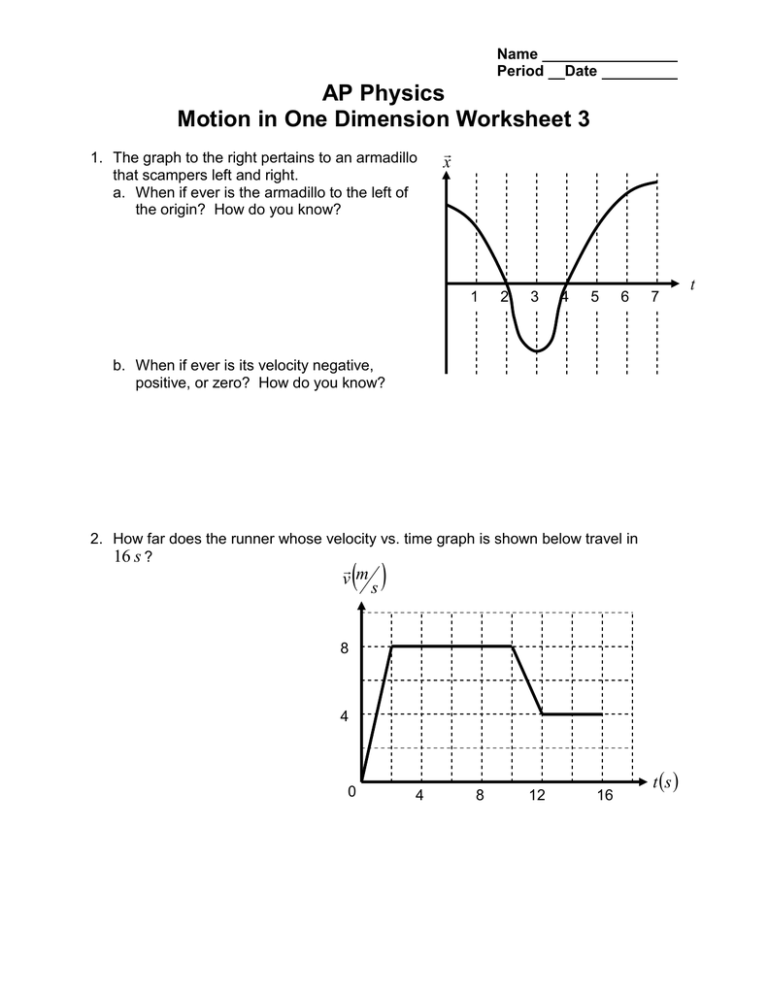
Linearization is a fundamental concept in Advanced Placement Physics, particularly when dealing with non-linear relationships in experimental data. Mastering linearization is not only key to understanding complex physical phenomena but also crucial for acing AP Physics exams. This blog post will guide you through five expert tricks to excel in AP Physics linearization worksheets.
Understanding Linearization

Before diving into the tricks, it’s essential to grasp the concept of linearization:
- What is Linearization? - Linearization transforms a non-linear function into a linear one to simplify analysis. This process helps students to apply calculus in more straightforward ways, especially when plotting graphs.
- Why It Matters? - In AP Physics, linearizing data allows you to determine physical constants or properties from experimental data, enhancing the accuracy of your measurements and calculations.
Trick 1: Identify the Form

Before you start linearizing, recognize the type of non-linear relationship you’re dealing with:
- Polynomial (quadratic, cubic, etc.): ( y = ax^n + bx^{n-1} + … + c )
- Exponential: ( y = ae^{bx} )
- Power Law: ( y = ax^b )
Once you’ve identified the form, you can decide on the proper linearization technique. For example, to linearize ( y = ax^2 + bx + c ), you might need to plot ( y ) versus ( x^2 ).
Trick 2: Use Logarithms

Logarithms are incredibly useful for dealing with exponential and power law functions:
- Exponential Functions: To linearize ( y = ae^{bx} ), take the natural log of both sides: ( \ln(y) = \ln(a) + bx ). Now, plot (\ln(y)) versus (x).
- Power Law Functions: For ( y = ax^b ), apply log to both sides to get ( \ln(y) = \ln(a) + b\ln(x) ), then plot (\ln(y)) versus (\ln(x)).
🔎 Note: Always check the units of your data before plotting. Ensure they're consistent or appropriately scaled.
Trick 3: Graphical Techniques

Graphical analysis is at the core of linearization:
- Linearization by Manipulation: For functions like ( y = x^2 ), plot ( y ) versus ( x^2 ). The slope will yield the ‘a’ value, while the intercept gives ‘c’.
- Curve Fitting: Modern tools allow for fitting curves directly. However, understanding the underlying math helps in choosing the correct fit.
Here’s a simple table to clarify which graph to plot for different functions:
| Original Function | Linearized Function | Graphical Plot |
|---|---|---|
| ( y = ax^2 ) | ( y = kx^2 ) | Plot ( y ) vs ( x^2 ) |
| ( y = ae^{bx} ) | ( \ln(y) = bx + \ln(a) ) | Plot (\ln(y)) vs ( x ) |

Trick 4: Error Propagation

Error analysis is not just about accuracy but also about understanding the limits of your linearized model:
- Error in Linearization: When manipulating data, errors in the original measurements propagate through the linearization process. Always estimate errors for your linear model.
🔎 Note: Use the root mean square (RMS) or similar statistical methods to account for error propagation in your linearized models.
Trick 5: Practice and Verify

Finally, repetition and verification are keys to mastering linearization:
- Worked Examples: Go through as many real-world physics problems as possible. Practicing different scenarios helps in understanding the nuances.
- Verification: After linearizing, verify your results by substituting back into the original equation. A small error is expected due to approximations, but significant discrepancies might indicate errors in your approach.
In conclusion, mastering AP Physics linearization involves a blend of theoretical understanding and practical application. By following these tricks, you can transform complex relationships into linear equations, making analysis and prediction much more manageable. The key is to identify the form of the function, use logarithms, apply graphical techniques, understand error propagation, and consistently practice and verify your work.
What is the difference between linear and non-linear relationships in physics?

+
Linear relationships imply that a change in one variable results in a proportional change in another variable. Non-linear relationships, however, do not follow this rule, and the change can be exponential, logarithmic, or follow a different pattern altogether.
Why is linearization important in AP Physics?

+
Linearization simplifies complex data analysis, making it easier to apply calculus and other mathematical tools to understand and predict physical phenomena.
How does error propagate in linearized models?

+
Errors in the original measurements propagate through mathematical operations used in linearization. Methods like RMS help to estimate the compounded error in the linear model.
Can all functions be linearized?

+
Most common physical functions can be linearized, especially those involving exponential, polynomial, or power law relationships. However, some highly complex or non-standard functions might resist simple linearization techniques.
What should I do if my data doesn’t fit a linear model?

+
If your data does not fit a linear model, review your data collection process for errors, ensure you’ve applied the correct linearization technique, or consider using more complex fitting methods like polynomial or spline fitting.