5 Essential Answers for Inscribed Angles Worksheet
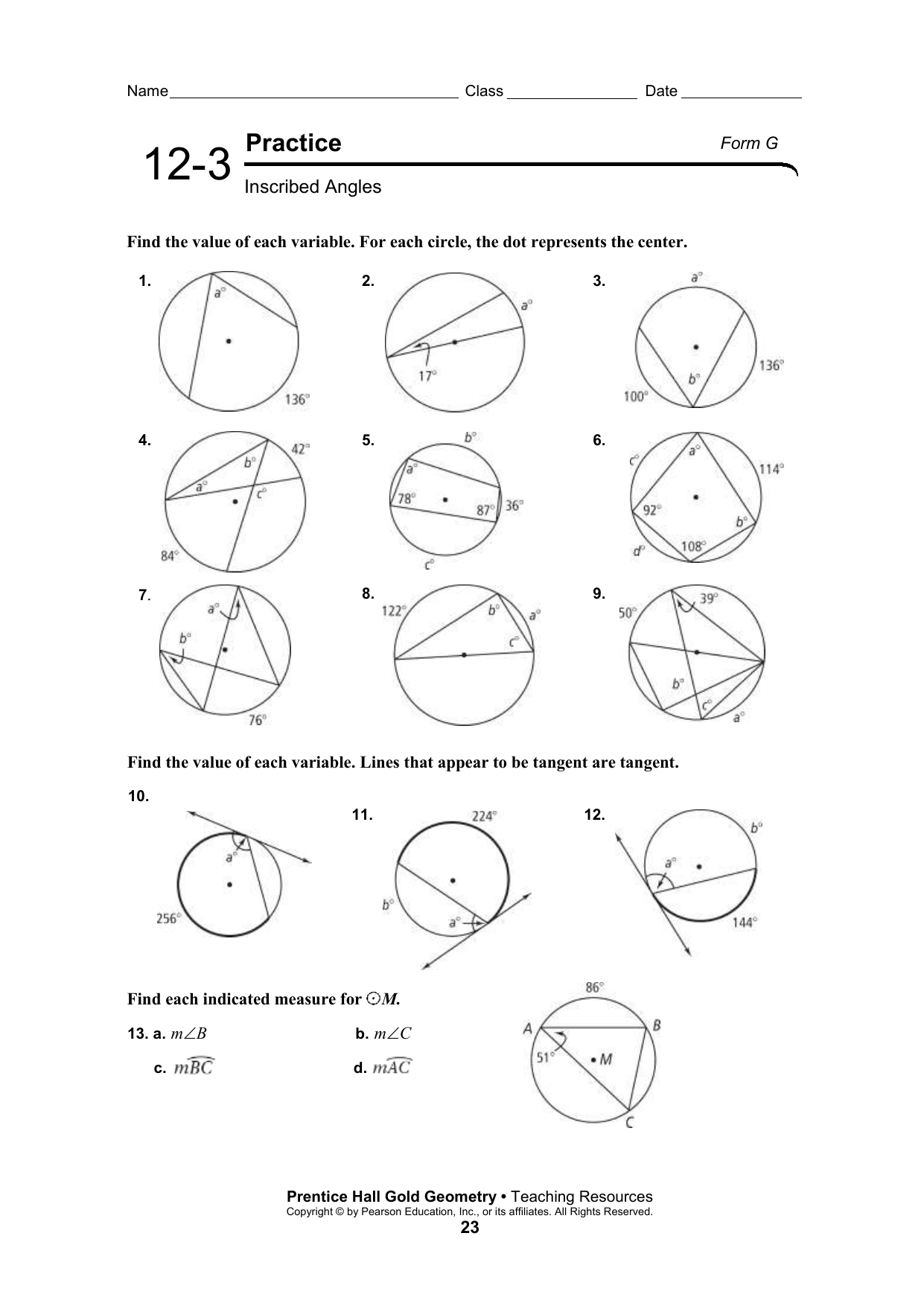
Understanding inscribed angles in geometry can be pivotal for students diving into more complex mathematical concepts. An inscribed angle in a circle is one where its vertex lies on the circumference, and its two sides are chords of the circle. Here, we'll delve into five essential questions that often appear on inscribed angles worksheets, providing detailed explanations and solutions to enhance comprehension and mastery of this topic.
1. What is an Inscribed Angle?
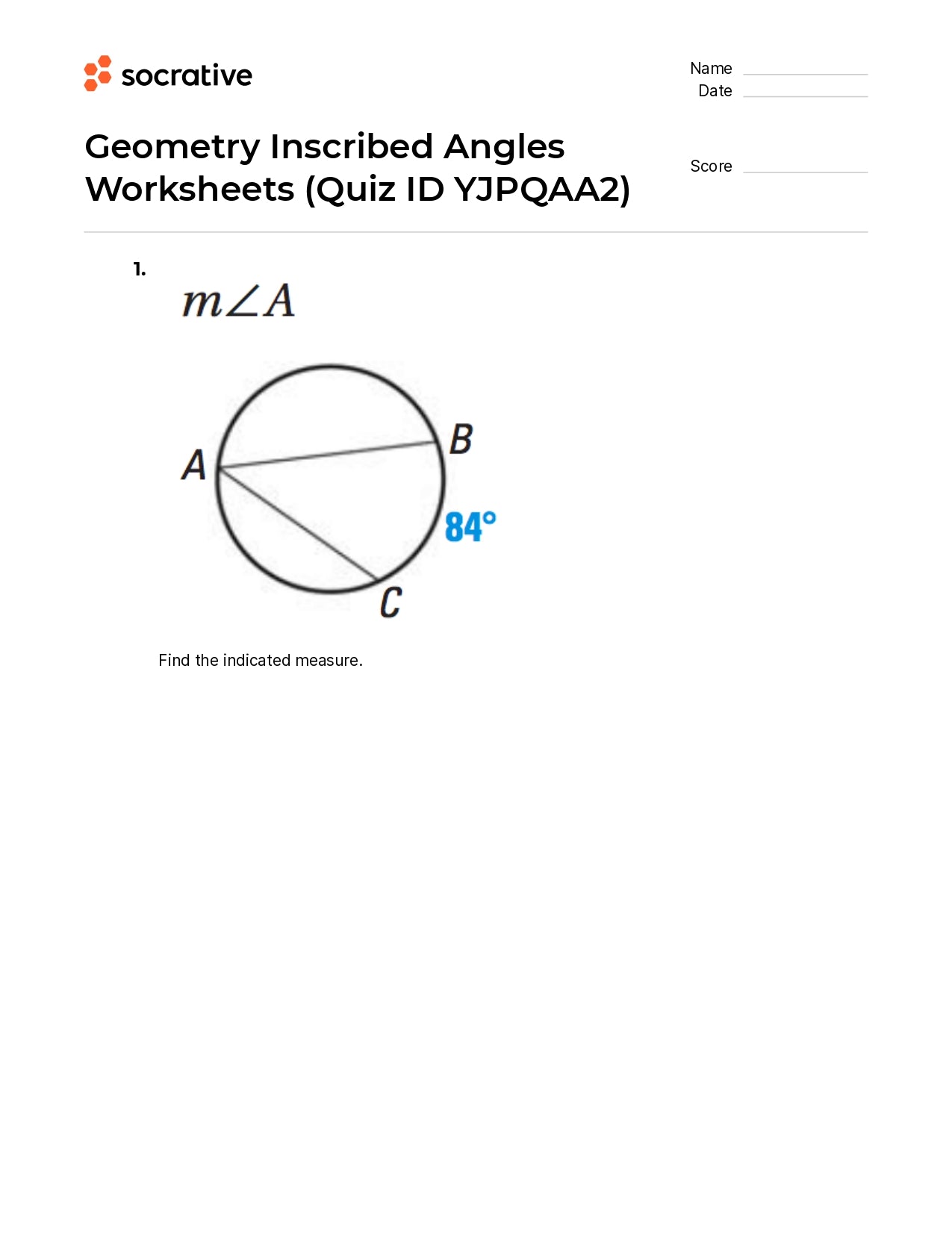

An inscribed angle is formed when two chords of a circle intersect at a point on the circle itself. Here’s how to recognize it:
- Vertex: The vertex is on the circumference.
- Sides: Two sides of the angle are chords.
- Measurement: The angle measures half the arc it intercepts.
💡 Note: An inscribed angle that intercepts a semicircle will always measure 90°.
2. How Do You Find the Measure of an Inscribed Angle?
To calculate the measure of an inscribed angle:
- Identify the Intercepted Arc: The arc is the part of the circle’s circumference between the endpoints of the two chords.
- Halve the Arc: The angle’s measure is half the measure of this arc in degrees.
| Arc Measure | Inscribed Angle |
|---|---|
| 60° | 30° |
| 90° | 45° |

3. Can Two Inscribed Angles Intercepting the Same Arc Be Equal?

Yes, two inscribed angles that intercept the same arc will be equal in measure:
- They both subtend the same arc, hence they will have identical angle measurements.
4. What Happens If the Inscribed Angle is Formed by Tangents?
When one or both sides of an inscribed angle are tangents to the circle:
- The angle between a tangent and a chord through the point of tangency is equal to the angle in the alternate segment.
5. How Does the Location of the Vertex Affect the Angle Measurement?

The position of the vertex significantly impacts the inscribed angle’s measure:
- On the Circle: As discussed, it measures half of the intercepted arc.
- Inside the Circle: If the vertex is inside the circle, the angle measures half the sum of the measures of the arcs intercepted by its sides.
- Outside the Circle: If the vertex is outside, the angle measures half the difference between the larger and smaller intercepted arcs.
🔄 Note: Moving the vertex along the circumference while keeping the arc the same will not change the inscribed angle’s measure.
The understanding of inscribed angles is crucial not just for solving problems but also for grasping more advanced geometrical concepts. This foundational knowledge helps in understanding cyclic quadrilaterals, properties of circles, and various theorems related to angles. By mastering these five essential answers, students can approach their inscribed angles worksheets with confidence, knowing how to find angles, understand their properties, and apply them in different contexts.
What if an inscribed angle intersects multiple arcs?
+
If an inscribed angle intersects multiple arcs, the angle measure is still calculated as half the measure of the arc it most directly intercepts.
Do all inscribed angles in a circle sum up to 360°?

+
Not necessarily. The sum of inscribed angles depends on the arcs they intercept, not their total coverage of the circle.
How do inscribed angles differ from central angles?

+
Central angles have their vertex at the center of the circle, whereas inscribed angles have their vertex on the circle’s circumference. The central angle measures the arc it intercepts directly, while an inscribed angle measures half of its intercepted arc.