5 Essential Tips for Mastering Angles in Circles
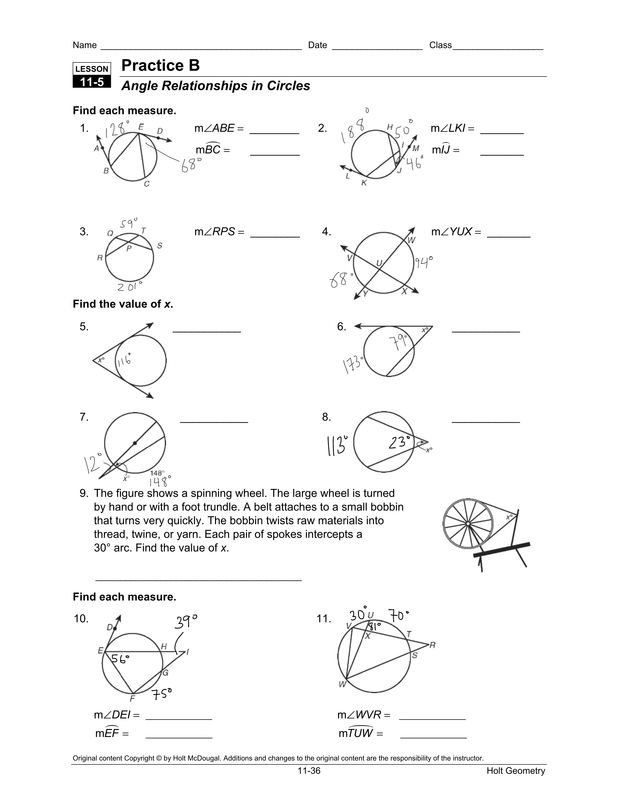
The world of geometry unveils its most intriguing secrets in the form of angles in circles. These angles, whether they're inscribed or central, hold a treasure trove of mathematical wonders. Mastering these angles not only boosts your geometric prowess but also offers a profound understanding of how shapes interact with each other. In this comprehensive guide, we'll explore five essential tips to help you understand and calculate these angles with ease and precision.
The Difference Between Inscribed and Central Angles

Before diving into the tips, it’s crucial to understand the distinction between inscribed and central angles:
- Central Angle: An angle whose vertex is at the center of the circle and whose arms pass through the circumference.
- Inscribed Angle: An angle whose vertex is on the circle’s circumference and whose arms pass through two other points on the circle.
Here are five essential tips to master angles in circles:
Tip 1: Understand the Angle Measure Relationship


One of the most fundamental principles in circle geometry is the relationship between central and inscribed angles:
- The measure of a central angle is equal to the measure of the arc it intercepts.
- An inscribed angle measures half the arc it intercepts.
📚 Note: This relationship simplifies many circle calculations, making it easier to find unknown angles.
Tip 2: Utilize the Theorem of Opposite Angles

Inscribed angles that intercept the same arc are equal. This theorem is particularly useful in circles with many inscribed angles:
- If two angles intercept the same arc, their measures are the same.
- This property can be used to solve for multiple angles with a single arc measurement.
| Example | Inscribed Angle 1 | Arc Measure | Inscribed Angle 2 |
|---|---|---|---|
| Situation | 60° | 120° | 60° |

💡 Note: This theorem helps in simplifying complex geometric problems by establishing a consistent measure for angles that intercept the same arc.
Tip 3: Work with Cyclic Quadrilaterals
Cyclic quadrilaterals, which are quadrilaterals inscribed in a circle, follow a particular rule:
- The opposite angles in a cyclic quadrilateral sum to 180°.
- This can simplify calculations where you know only one of the angles.
This property allows you to deduce one unknown angle if the opposite one is known:
- If one angle is 90°, the opposite angle must also be 90°.
Tip 4: Tangent and Angle Relationships

Angles formed by tangents and chords or secants have specific relationships:
- An angle formed by a tangent and a chord at the point of tangency equals the inscribed angle that intercepts the same arc.
- Angles formed by two secants, two tangents, or one of each, have formulas for their measures.
Using these relationships:
- Tangent-Secant: (m∠ABC = 1⁄2(|arc AD| - |arc BC|)) where A, B, and C are points on the circle, and D is on the circumference.
- Secant-Secant: (m∠ABC = 1⁄2(|arc AC| - |arc BD|)) where A, B, C, and D are points on the circle.
- Tangent-Tangent: (m∠ABC = 1⁄2(|arc AB| - |arc CD|)) where A, B, and C are points on the circle, and D is the point of intersection.
📝 Note: These relationships expand your geometric toolkit, allowing for the solution of more complex problems involving circles and tangents.
Tip 5: Practice, Practice, Practice

Like any skill, mastering angles in circles requires:
- Consistent practice with varied problems.
- Exploring real-life applications.
- Using visual aids or diagrams to understand angle placement and measurements.
Consider:
- Solving textbook problems or online geometry quizzes.
- Participating in geometry discussions or forums.
- Utilizing geometric software for interactive learning.
🚀 Note: The more you practice, the more intuitive these angle relationships will become.
In essence, understanding angles in circles enriches our comprehension of geometry's broader landscape. By integrating the principles of central and inscribed angles, exploring opposite angles, cyclic quadrilaterals, and tangent-chord relationships, you've laid the foundation for geometric mastery. Moreover, the consistent practice is the key to achieving proficiency in this fascinating field of mathematics.
What is the difference between a central angle and an inscribed angle?
+
A central angle has its vertex at the center of the circle and measures the same as the arc it intercepts, while an inscribed angle has its vertex on the circle’s circumference and measures half the arc it intercepts.
How do I find an inscribed angle?

+
To find an inscribed angle, measure the intercepted arc and divide that measure by 2. For example, if an arc measures 120°, the inscribed angle would be 60°.
Why is the practice of circle geometry important?

+
Practicing circle geometry helps in mastering angle relationships, understanding real-life applications, and solving complex problems efficiently.


