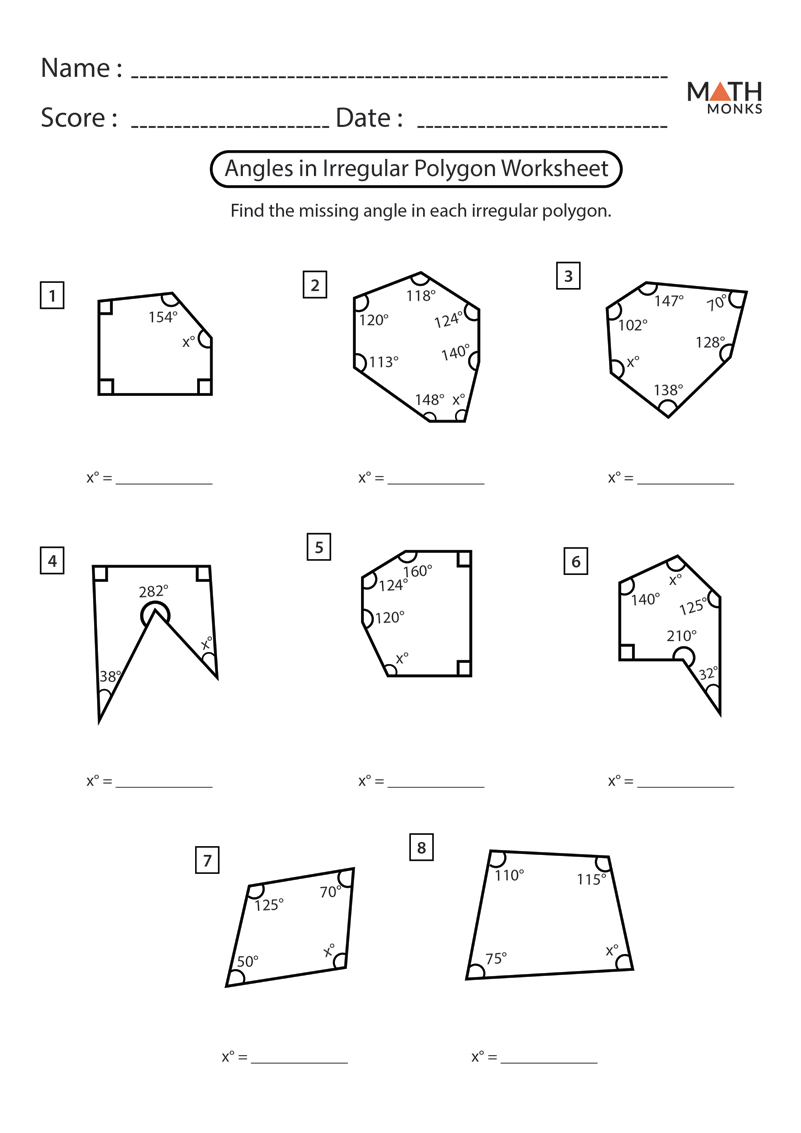
7 Key Angles in Polygons Worksheet Answers

Welcome to this comprehensive guide on understanding polygons and their angles. If you've been exploring polygons and are curious about their angles or are preparing for an exam, this blog post will provide you with detailed explanations, answers, and insightful notes. Let's delve into the world of polygons and explore the 7 key angles involved.
What Are Polygons?


Polygons are geometric figures that are closed, plane figures with straight sides or edges. They are crucial in mathematics for their regular structure and the ease with which we can calculate their properties. Here are the basic types of polygons:
- Triangle: 3 sides
- Quadrilateral: 4 sides
- Pentagon: 5 sides
- Hexagon: 6 sides
- Heptagon: 7 sides
- Octagon: 8 sides
- Nonagon: 9 sides
- Decagon: 10 sides
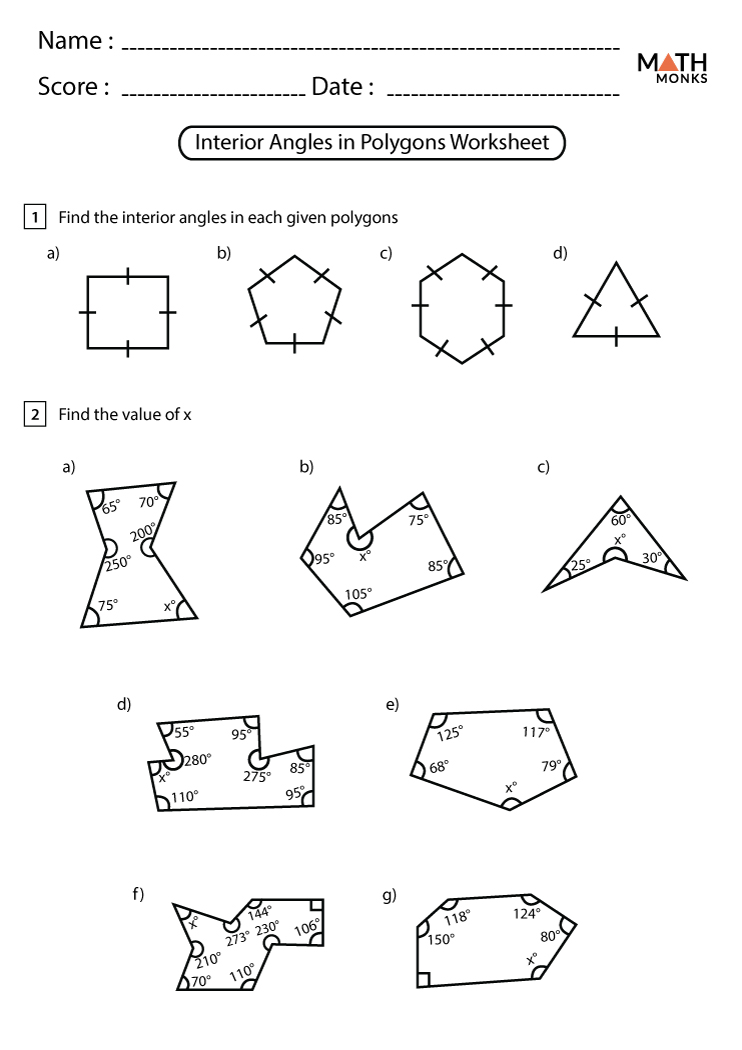
Types of Angles in Polygons

Polygons contain various types of angles. Here are the seven key angles that you need to know:
Interior Angles

The interior angle of a polygon is the angle formed inside the polygon at any vertex. Here’s how you can calculate the total sum of interior angles:
- For a polygon with n sides, the sum of interior angles is (n-2) \times 180°.
📝 Note: Remember, this formula applies to any polygon, regardless of how regular or irregular it is.
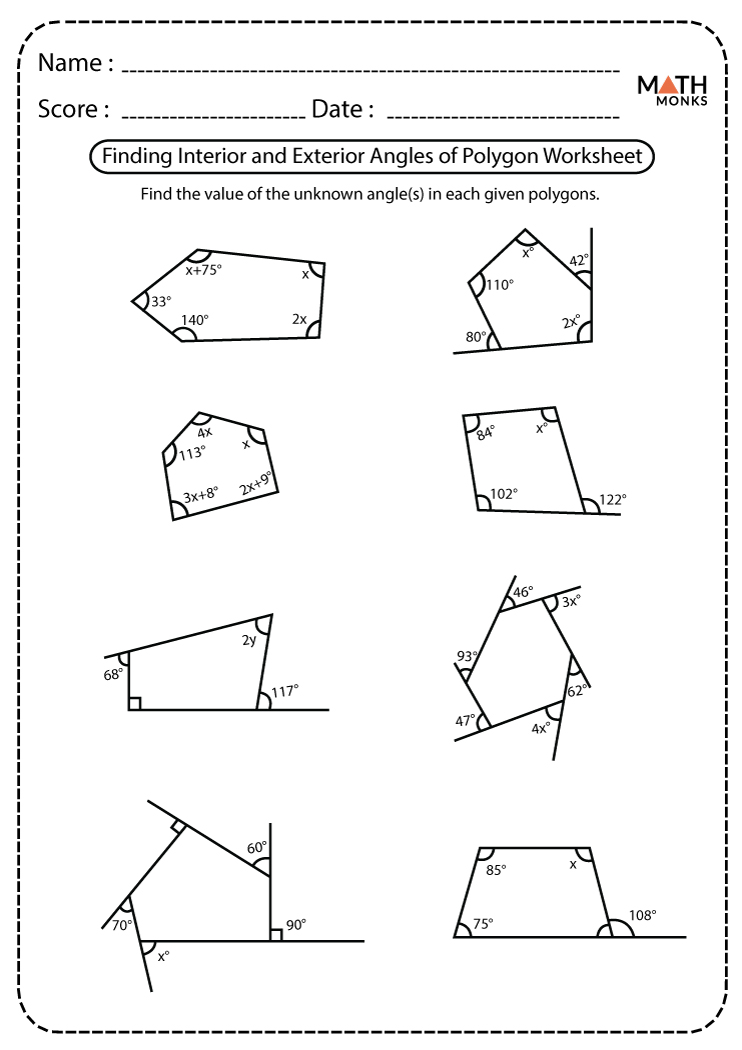
Exterior Angles
These are angles formed by one side of the polygon and the extension of an adjacent side. For all polygons, the sum of exterior angles is always:
- 360° regardless of the number of sides.
Central Angles

If you draw lines from the center of an inscribed circle to each vertex of a regular polygon, you’ll form central angles. Each central angle of a regular ( n )-sided polygon is:
- \frac{360°}{n}
Inscribed Angles
An inscribed angle is formed by two chords of a circle that share an endpoint. In the context of polygons, the chord would be a side of the polygon, and the angle subtends the opposite side. In a regular polygon, all inscribed angles on the same arc are equal.
Sum of Angles in Regular Polygons

Regular polygons have all sides and angles equal. Here are some formulas to find angles in regular polygons:
| Type of Polygon | Formula for Interior Angle | Formula for Central Angle |
|---|---|---|
| Equilateral Triangle | 60° | 120° |
| Square | 90° | 90° |
| Regular Pentagon | 108° | 72° |
| Regular Hexagon | 120° | 60° |

Angle Sum of All Interior Angles of Polygons

Here’s a look at the sum of all interior angles for different polygons:
- Triangle (3 sides): 180°
- Quadrilateral (4 sides): 360°
- Pentagon (5 sides): 540°
- Hexagon (6 sides): 720°
- Heptagon (7 sides): 900°
Properties of Polygons’ Angles

Here are some important properties to keep in mind:
- Each interior angle of a regular polygon can be found by dividing the sum of interior angles by the number of sides, n .
- The sum of the exterior angles is constant at 360°, and each exterior angle in a regular polygon is \frac{360°}{n} .
This understanding of the angles in polygons will help you excel in geometry, from basic shapes to the most complex figures.
Practical Applications

Polygons and their angles have real-world applications in:
- Architecture, for designing buildings with specific angular structures
- Art, where angles create visual effects and patterns
- Engineering, for creating polygons that distribute forces evenly
- Navigation, where understanding angles helps in creating efficient flight paths
💡 Note: Recognizing the angles in polygons can simplify many real-world problem-solving tasks.
Exploring Polygons Through Angles
By examining the angles in polygons, we not only appreciate their symmetrical beauty but also understand how to calculate and predict properties:
- Interior and exterior angles relate to the number of sides, helping us understand symmetry and regularity.
- Central and inscribed angles allow for calculations involving circle inscribed within or circumscribing the polygon.
- These relationships are vital for everything from mathematical proofs to design work.
This exploration concludes our in-depth look at the 7 key angles in polygons. Understanding these angles opens up a world of geometric possibility, helping you solve problems, design, and even appreciate art and architecture from a new perspective.
How do you calculate the interior angle of a regular polygon?

+
To find the measure of each interior angle of a regular ( n )-sided polygon, use the formula: (\frac{(n-2) \times 180°}{n}).
Can the sum of exterior angles of any polygon be greater or less than 360°?

+
The sum of the exterior angles of any polygon, regular or irregular, is always exactly 360°.
What’s the difference between central and inscribed angles?
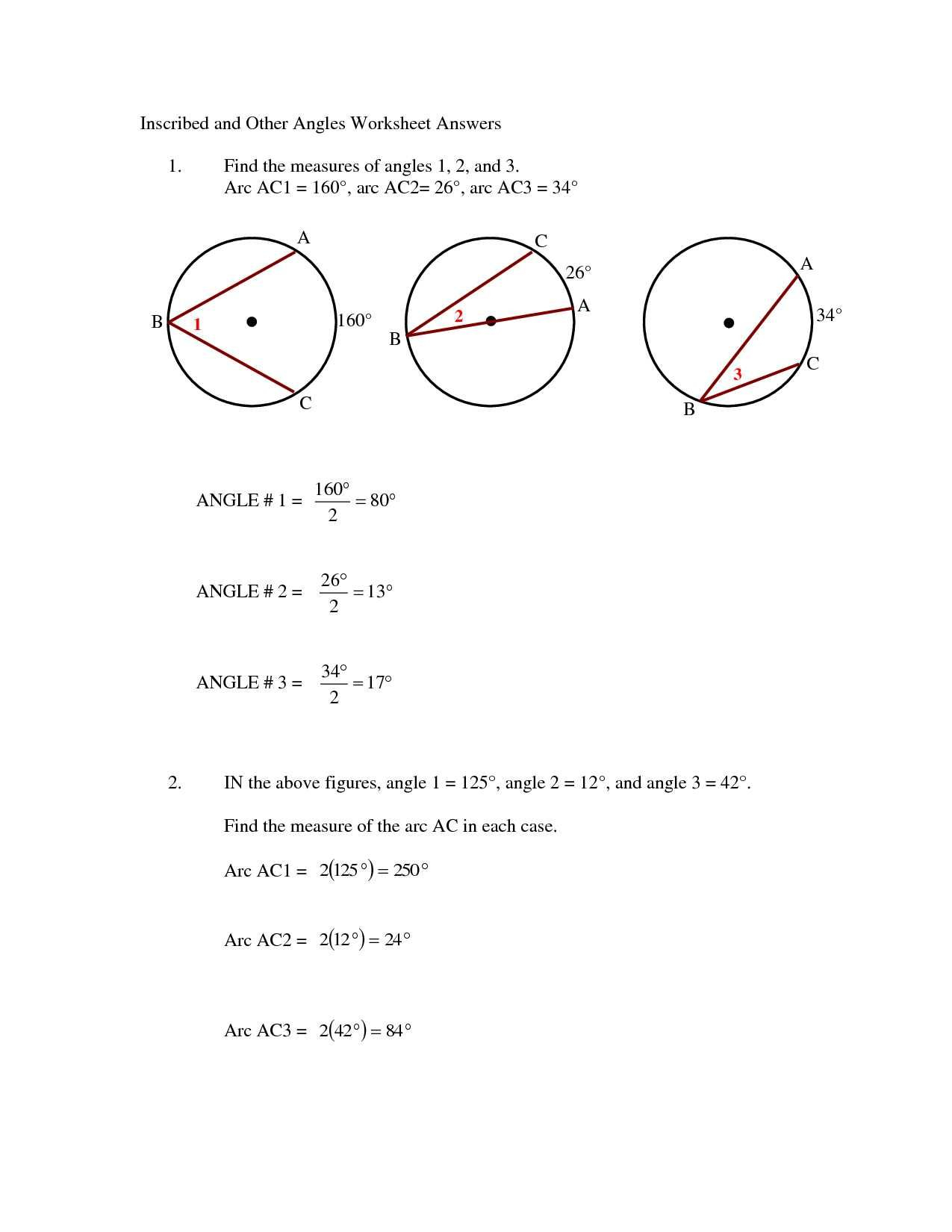
+
A central angle has its vertex at the center of the circle with sides being the radii of the circle, while an inscribed angle’s vertex is on the circumference of the circle with sides being two chords.
Why do interior angles of polygons matter?
+Understanding interior angles helps in various practical applications like design, where the angles influence the shape’s stability and visual appeal.
How can angles of polygons be used in everyday life?
+Angles in polygons are used in construction to design walls, in games to create regular shapes, in navigation for efficient route planning, and in art for creating symmetrical patterns.