5 Ways to Master Angles Formed by a Transversal

When two parallel lines are intersected by a third line, called a transversal, various angles are formed. Mastering the properties of these angles is crucial for solving problems in geometry and other areas of mathematics. In this article, we will explore five ways to master angles formed by a transversal.
Understanding the Basics

Before diving into the five ways to master angles formed by a transversal, it’s essential to understand the basic properties of parallel lines and transversals. When two parallel lines are intersected by a transversal, eight angles are formed. These angles can be classified into several types, including corresponding angles, alternate interior angles, alternate exterior angles, and interior angles on the same side of the transversal.
1. Corresponding Angles

Corresponding angles are angles that are in the same relative position in each intersection. For example, if two parallel lines are intersected by a transversal, the angles formed in the top left and bottom left positions are corresponding angles. To master corresponding angles, remember that they are always equal in measure.
- Example: In the diagram below, ∠A and ∠D are corresponding angles. Since the lines are parallel, ∠A = ∠D.
| ∠A | ∠B | ∠C | ∠D |
| Parallel lines intersected by a transversal | |||

2. Alternate Interior Angles

Alternate interior angles are angles that are inside the parallel lines and on opposite sides of the transversal. To master alternate interior angles, remember that they are always equal in measure.
- Example: In the diagram below, ∠B and ∠C are alternate interior angles. Since the lines are parallel, ∠B = ∠C.
3. Alternate Exterior Angles
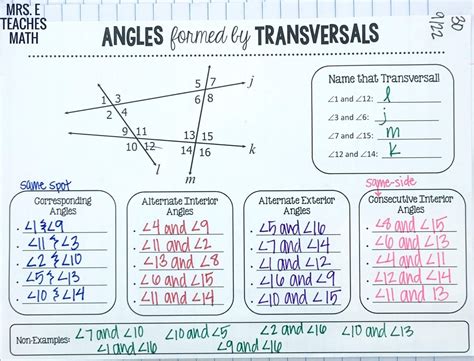
Alternate exterior angles are angles that are outside the parallel lines and on opposite sides of the transversal. To master alternate exterior angles, remember that they are always equal in measure.
- Example: In the diagram below, ∠A and ∠E are alternate exterior angles. Since the lines are parallel, ∠A = ∠E.
4. Interior Angles on the Same Side of the Transversal

Interior angles on the same side of the transversal are angles that are inside the parallel lines and on the same side of the transversal. To master interior angles on the same side of the transversal, remember that they are supplementary (add up to 180°).
- Example: In the diagram below, ∠B and ∠C are interior angles on the same side of the transversal. Since the lines are parallel, ∠B + ∠C = 180°.
5. Using the Properties to Solve Problems

Mastering the properties of angles formed by a transversal is crucial for solving problems in geometry. By applying the properties of corresponding angles, alternate interior angles, alternate exterior angles, and interior angles on the same side of the transversal, you can solve a wide range of problems.
- Example: In the diagram below, find the measure of ∠X.
| ∠A | ∠B | ∠C | ∠X |
| Parallel lines intersected by a transversal | |||
Since ∠A and ∠X are corresponding angles, ∠A = ∠X. Since ∠A = 60°, ∠X = 60°.
📝 Note: Always read the problem carefully and identify the given information before applying the properties of angles formed by a transversal.
In conclusion, mastering angles formed by a transversal is essential for solving problems in geometry. By understanding the properties of corresponding angles, alternate interior angles, alternate exterior angles, and interior angles on the same side of the transversal, you can solve a wide range of problems. Remember to always apply the properties correctly and use the given information to find the solution.
What is a transversal?
+
A transversal is a line that intersects two or more other lines.
What are corresponding angles?

+
Corresponding angles are angles that are in the same relative position in each intersection.
What are alternate interior angles?

+
Alternate interior angles are angles that are inside the parallel lines and on opposite sides of the transversal.
Related Terms:
- transversals angles worksheet pdf
- transversal angles cheat sheet