Unlock Geometry: Angle Relationships Worksheets for Mastery
Learning geometry can be a thrilling journey into the world of shapes and measurements, where the understanding of angles opens up new dimensions of spatial awareness. Angle relationships are at the heart of this subject, connecting various geometric figures in ways that are both elegant and essential for practical applications. Whether it's solving architectural problems, navigating through complex polygons, or simply understanding the world around us, mastering angle relationships is key. Let's dive into how worksheets can be an effective tool for gaining this mastery.
Understanding Angle Relationships

Before we delve into how to work with these relationships, it’s crucial to understand what angle relationships are. Here are some key concepts:
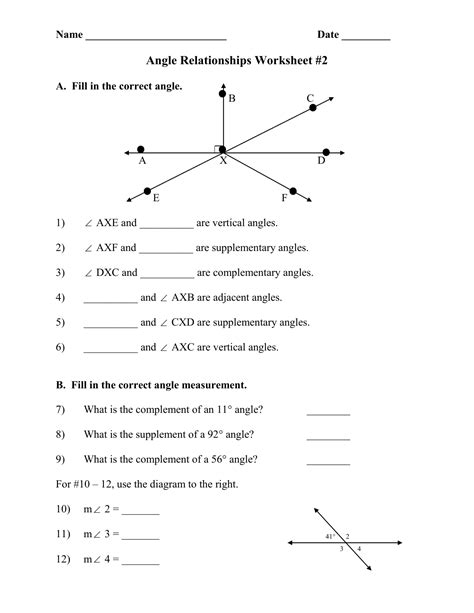
- Adjacent Angles: Angles that have a common vertex and share a side, but no overlap. Example: angles formed by intersecting lines.
- Vertical Angles: Non-adjacent angles formed by two intersecting lines. They are always equal in measure.
- Supplementary Angles: Two angles that add up to 180 degrees. A linear pair is an example of this relationship.
- Complementary Angles: Two angles whose measures add up to 90 degrees.
- Interior Angles: Angles that lie inside a pair of lines cut by a transversal.
- Exterior Angles: Angles outside a pair of lines cut by a transversal.
- Alternate Interior Angles: Non-adjacent interior angles on opposite sides of the transversal; they are congruent if the lines are parallel.
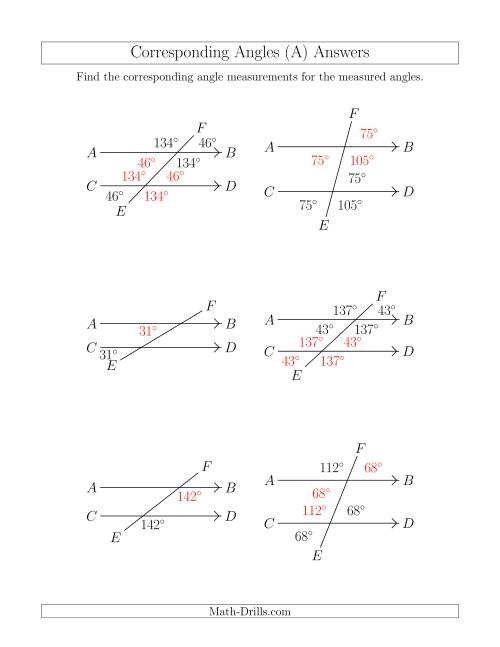
- Corresponding Angles: Located on the same side of the transversal and in the same relative position; they are congruent if the lines are parallel.
Mastering these concepts involves not just recognizing them but also understanding their implications in various geometric configurations.
📝 Note: Understanding these relationships is foundational for all advanced geometric reasoning.
Designing Effective Worksheets
A well-designed worksheet not only reinforces learning but also makes the process engaging and clear. Here’s how to design one:
- Visual Aids: Use diagrams or illustrations to present angle relationships. Diagrams should be clear and scaled appropriately.
- Incremental Difficulty: Start with straightforward problems and gradually increase complexity. This ensures learners can build confidence before tackling more challenging scenarios.
- Practical Context: Include problems that reflect real-world situations where angle relationships are applied, like architecture or map-reading.
- Interactive Elements: Add sections where students can fill in missing angles or label different types of angles, fostering an active learning environment.
- Assessment Rubrics: Provide clear criteria for correct answers to guide learning and self-assessment.
- Variety in Formats: Use a mix of fill-ins, multiple-choice, and true/false statements to assess different aspects of understanding.
Utilizing Worksheets for Mastery

The effective use of worksheets involves a systematic approach:
- Practice Sets: Provide varied practice sets for each angle relationship. This repetition ensures understanding and retention.
- Problem-Solving Exercises: Encourage the application of known angle relationships to solve unfamiliar problems, promoting critical thinking.
- Error Identification: Include exercises where students must find and correct errors in given answers, reinforcing accuracy.
- Group Activities: Develop worksheets with questions or scenarios where students work together, enhancing collaborative learning.
- Application to Real Life: Set problems in real-world contexts, like calculating angles in buildings or landscapes, making learning relevant and engaging.
🔍 Note: Continuous practice with these worksheets can significantly enhance a student’s ability to visualize and solve geometric problems.
Common Pitfalls and How to Address Them

Here are some common issues students face with angle relationships and tips for overcoming them:
- Misidentification: Students might confuse different types of angles or their relationships. Use clear labeling and visual aids to differentiate.
- Parallel Line Assumptions: Some might assume lines are parallel when they aren’t. Always emphasize the need to verify or be given this information.
- Angle Measurement Errors: Often due to misreading protractors or misunderstanding angle notation. Regular practice with protractor use and angle identification helps.
- Lack of Understanding: If concepts like “sum of angles in a triangle” are not internalized, problems become complex. Introduce and review these fundamentals frequently.
Progression in Learning

Angle relationships learning should be progressive:
- Basic Identification: Start with recognizing angles in simple figures.
- Relationships and Properties: Teach the properties of different types of angles and their relationships.
- Application to Geometry: Move to more complex geometric shapes where these relationships play a crucial role.
- Real-World Application: Use real-life problems to illustrate the importance of angle relationships.
- Proving and Deriving: End with proofs and derivations, which require deep understanding of angle relationships.
Why are angle relationships important?

+
Angle relationships form the basis for understanding more complex geometric shapes, constructions, and real-world applications like architecture and engineering.
How can I make learning angle relationships fun?

+
By integrating real-life scenarios, puzzles, and interactive group activities, learning becomes more engaging and relatable for students.
What are common mistakes students make?

+
Students often misidentify angles, assume parallel lines without verification, or struggle with angle measurements due to incorrect use of tools like protractors.
Mastering angle relationships through well-designed worksheets can transform the learning experience into an engaging, insightful journey into the world of geometry. By understanding these fundamental principles, students not only excel in their geometry courses but also gain tools applicable in various fields. This process not only enhances their spatial reasoning but also equips them with problem-solving skills vital for future academic and professional challenges.



