7 Must-Know Angle Relationships in Circles Explained
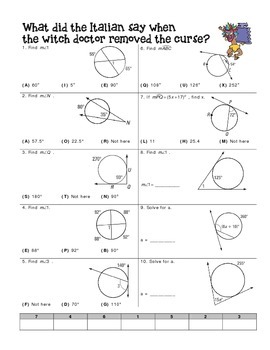
Understanding the geometric relationships within circles is fundamental not only for students of geometry but also for anyone interested in architecture, engineering, art, or simply exploring the beauty of mathematics. Circles are not just simple curves; they host a variety of angular relationships that play a crucial role in various applications. Let's dive into seven must-know angle relationships in circles that will enhance your understanding and appreciation of this versatile shape.
Inscribed Angles

An inscribed angle is an angle whose vertex lies on the circumference of a circle, and whose sides intersect the circle at two points. The key relationship here is:
- The measure of an inscribed angle is half the measure of the central angle that subtends the same arc.
This theorem simplifies how we calculate angles in circles, making problem-solving more intuitive.
Central Angles

A central angle has its vertex at the center of the circle, and its sides extend to two points on the circle’s circumference. Here’s what you need to know:
- The central angle equals the measure of the arc it subtends.
- A circle is 360°, so dividing it into segments with central angles helps in understanding and partitioning the circle.
Angles in a Semicircle

An angle inscribed in a semicircle is a special case of an inscribed angle:
- Any angle inscribed in a semicircle is a right angle, or 90°.
- This relationship makes the semicircle a useful geometric figure in construction and design.
Angles Intercepted by Parallel Chords

When two chords in a circle are parallel, the intercepted arcs and the angles they form have interesting properties:
- Angles formed by the intersection of two parallel chords with the circumference of the circle are congruent.
- The arcs intercepted by these chords are equal in measure.
Angles Between a Tangent and a Chord
The angle formed by a tangent and a chord at the point of tangency is an external angle with some unique properties:
- This angle equals the measure of the arc opposite to it on the other side of the chord.
- This relationship is useful in solving problems involving tangents and chords.
Secant-Secant Angle

When two secant lines intersect inside a circle, the measure of the angle formed between the two secants:
- Is half the sum of the measures of the arcs intercepted by the angle.
Secant-Tangent Angle

This relationship involves one secant line and one tangent line intersecting outside the circle:
- The angle formed equals half the difference of the measures of the intercepted arcs.
In understanding these angle relationships in circles, one appreciates the elegance and interconnectedness of geometric principles. Whether you're tackling a complex geometry problem, designing circular elements in engineering or art, or simply curious about mathematics, these relationships serve as building blocks for deeper exploration.
📌 Note: Remember, these relationships are not just mathematical abstractions but are often visible in real-life scenarios where circles and angles interact.
Having a firm grasp on these concepts not only makes solving problems related to circles more manageable but also enhances one's ability to visualize and manipulate spatial relationships in three dimensions. These insights into angle relationships in circles can transform the way you see and work with circular elements in various fields of study.
How do you know which angle relationship applies in a given circle problem?

+
Identify the key elements like tangents, chords, and arcs involved in your diagram. Match these elements to the descriptions of angle relationships.
Why is it important to learn about angles in circles?

+
Angles in circles are fundamental in fields like engineering, architecture, and design where circular shapes are prevalent.
Can these angle relationships help in real-world design?

+
Absolutely! From creating arches to designing wheels or circular windows, understanding these relationships ensures precise and visually pleasing results.