Unlocking Geometry: Angle and Segment Worksheet Answers

Geometry can be a captivating yet challenging subject, intertwining mathematical reasoning with visual creativity. To help students understand the core concepts of angles and segments, geometry worksheets are often utilized in educational settings. This post provides detailed insights into the solutions for common worksheet questions involving angles and line segments, ensuring students can grasp these fundamental geometrical principles with clarity.
Understanding Angles


Angles are essential in geometry. They define the rotation between two lines or segments. Here’s a breakdown of the key types:
- Acute Angle: An angle less than 90 degrees.
- Right Angle: Exactly 90 degrees, usually marked with a small square in diagrams.
- Obtuse Angle: Greater than 90 degrees but less than 180 degrees.
- Straight Angle: Exactly 180 degrees, forming a straight line.
- Reflex Angle: More than 180 degrees but less than 360 degrees.
Worksheet Angle Questions

Here are typical worksheet questions and their solutions:
| Question | Answer |
|---|---|
| What type of angle is formed when two straight lines intersect at a point? | A Right Angle. |
| Calculate the sum of the interior angles of a triangle. | 180 degrees. |
| An angle inside a triangle measures 35 degrees. How much is the remaining sum of the interior angles? | 145 degrees (180 - 35). |

Working with Segments


Line segments are another basic building block in geometry, representing portions of lines with finite lengths. Below are key concepts:
- Length: The distance between two endpoints.
- Midpoint: The point that divides a segment into two equal halves.
- Intersection: The point where two segments cross.
- Bisector: A line that divides a segment into two congruent parts.
Worksheet Segment Questions

Consider these common worksheet questions regarding line segments:
| Question | Answer |
|---|---|
| What is the length of a segment with endpoints at (2,3) and (5,6)? | The length is 5 units, calculated using the distance formula. |
| Two segments of lengths 10 and 15 units are joined. What’s the resulting segment’s length? | 25 units. |
| How do you find the midpoint of a segment? | By averaging the coordinates of the endpoints. |
👉 Note: When dealing with segments, ensure your measurements are accurate to maintain the integrity of the geometrical properties involved.
Key Techniques for Angle and Segment Problems

To excel in geometry, these techniques can be invaluable:
- Identifying Angle Relationships: Recognize pairs like complementary, supplementary, and vertical angles.
- Using Geometry Theorems: Apply the properties and postulates of parallel lines, transversals, and triangle congruence.
- Logical Reasoning: Understanding how to move from one geometric statement to another, making logical deductions.
- Visual Aids: Sketching diagrams or using geometric software can provide visual clarity.
Throughout your studies, remember that geometry problems often require a blend of mathematical calculation and visual analysis. By following these principles, you can tackle both angle and segment problems with greater confidence.
Applications of Geometry

Geometry extends beyond the classroom, touching various aspects of life and industry:
- Architecture: Designing structures and ensuring stability through calculations of load, balance, and angle placement.
- Art: Artists use geometry in perspective drawing, symmetry, and proportion.
- Navigation: Using angles to calculate distances, bearings, and to triangulate positions.
- Engineering: From civil to aerospace engineering, precise geometric measurements are crucial.
🌐 Note: Remember, geometry is not just about abstract shapes; it's a fundamental tool in real-world problem-solving.
The journey through geometry involves mastering both theoretical knowledge and practical application. Through geometry worksheets, students are equipped with the tools needed to visualize, calculate, and ultimately understand the world through geometric terms. Keep practicing, and you'll find that the principles of angles, segments, and beyond become second nature.
Why is it important to distinguish between different types of angles?
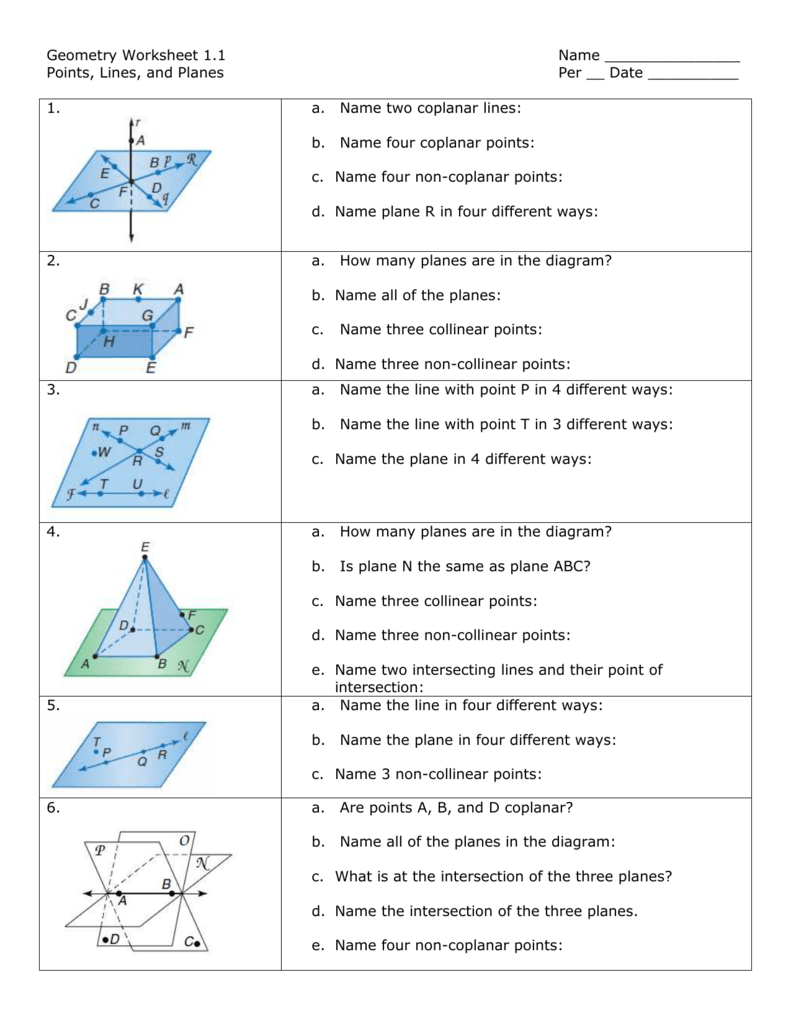
+
Differentiating between types of angles helps in understanding the spatial relationship between lines or segments, which is crucial for solving geometric problems, designing buildings, or even navigating real-world scenarios where angles matter.
How can understanding segments aid in problem-solving?

+
Segments provide measurements in geometry, helping to solve problems related to distances, midpoints, and coordinate geometry. Knowing how to work with segments allows for precise calculations in fields like architecture, engineering, and land surveying.
What are some common mistakes when solving angle and segment problems?

+
Common mistakes include misidentifying angles, incorrectly applying geometric properties or theorems, miscalculating segment lengths, and failing to use correct units of measurement or coordinate systems.
How can I improve my visualization skills in geometry?

+
Practice drawing, use geometric software for dynamic visualization, and try solving problems that require you to sketch or construct geometric figures from written descriptions.
Are there any online resources to help with geometry practice?

+
Yes, numerous websites offer interactive geometry problems, worksheets, video tutorials, and practice tools that can enhance your understanding and skills in geometry.