5 Ways to Master Angle Addition Postulate

Understanding the Angle Addition Postulate
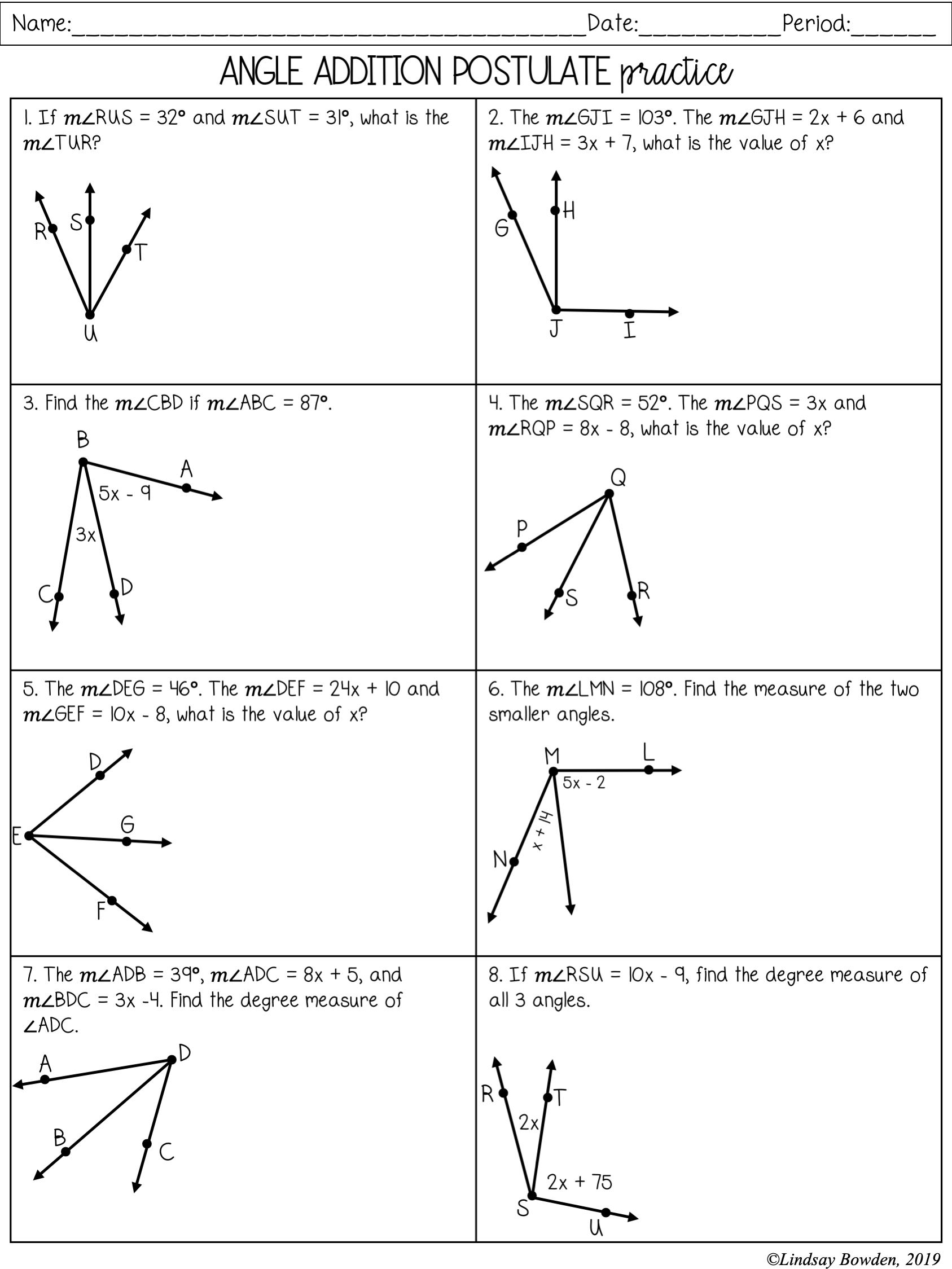
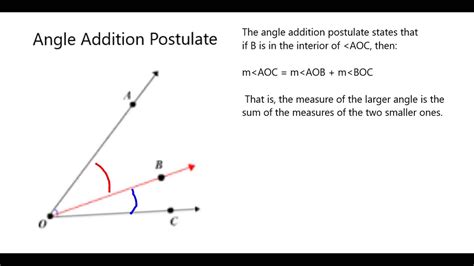
The Angle Addition Postulate is a fundamental concept in geometry that helps us determine the measure of an angle when we know the measures of its components. This postulate states that if point B is on line segment AC, then the measure of angle A plus the measure of angle C is equal to the measure of angle AOC. In simpler terms, the sum of the measures of two adjacent angles is equal to the measure of the larger angle formed by the two angles.
Visualizing the Angle Addition Postulate
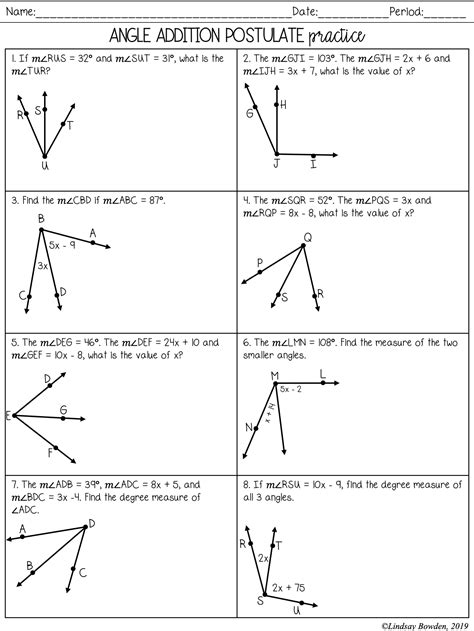
To better understand the Angle Addition Postulate, let’s take a look at a simple diagram. Suppose we have a line segment AC with point B on it. We can draw two angles, AOB and BOC, which are adjacent to each other.
| Angle AOB | Angle BOC | Angle AOC |
|---|---|---|
| ∠AOB = x° | ∠BOC = y° | ∠AOC = (x + y)° |
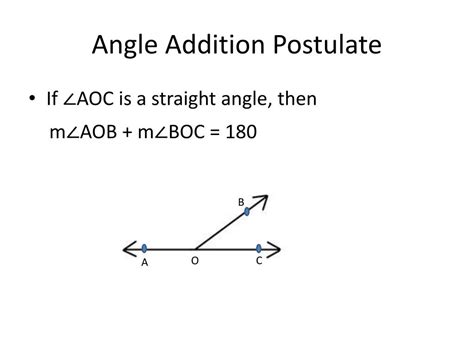
As we can see, the measure of angle AOC is equal to the sum of the measures of angles AOB and BOC.
5 Ways to Master the Angle Addition Postulate
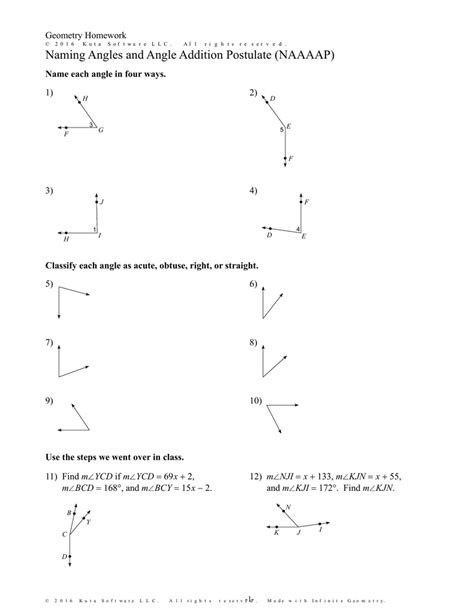
Now that we understand the concept of the Angle Addition Postulate, let’s look at five ways to master it.
1. Practice with Simple Angles

Start by practicing with simple angles, such as those that are adjacent to each other. For example, if you know that ∠AOB = 30° and ∠BOC = 60°, then you can use the Angle Addition Postulate to find the measure of ∠AOC.
∠AOC = ∠AOB + ∠BOC = 30° + 60° = 90°
2. Use Real-World Examples
The Angle Addition Postulate has many real-world applications, such as in architecture, engineering, and design. Try to think of examples where you can apply this concept. For instance, if you’re designing a building and you want to ensure that two walls meet at a 90° angle, you can use the Angle Addition Postulate to calculate the measures of the angles involved.
3. Create Your Own Diagrams

Creating your own diagrams is a great way to visualize the Angle Addition Postulate. Draw different angles and use the postulate to calculate the measures of the larger angles formed by the smaller angles. This will help you develop your problem-solving skills and become more confident in applying the postulate.
4. Practice with Multi-Step Problems

Once you’re comfortable with simple angles, move on to multi-step problems. These problems will require you to apply the Angle Addition Postulate multiple times to solve for the measure of a larger angle. For example:
∠AOB = 20° ∠BOC = 30° ∠COD = 40°
Find the measure of ∠AOD.
∠AOD = ∠AOB + ∠BOC + ∠COD = 20° + 30° + 40° = 90°
5. Apply the Postulate to Other Geometric Concepts
The Angle Addition Postulate is not just limited to angles. It can also be applied to other geometric concepts, such as triangles and polygons. For example, if you know the measures of two angles in a triangle, you can use the Angle Addition Postulate to find the measure of the third angle.
📝 Note: The Angle Addition Postulate is a fundamental concept in geometry, and mastering it will help you solve more complex problems in geometry and other areas of mathematics.
When explaining steps or tutorials, include important notes only when necessary. Avoid excessive notes.
What is the Angle Addition Postulate?

+
The Angle Addition Postulate states that if point B is on line segment AC, then the measure of angle A plus the measure of angle C is equal to the measure of angle AOC.
How can I practice the Angle Addition Postulate?

+
You can practice the Angle Addition Postulate by starting with simple angles, using real-world examples, creating your own diagrams, practicing with multi-step problems, and applying the postulate to other geometric concepts.
Why is the Angle Addition Postulate important?
+
The Angle Addition Postulate is important because it helps us determine the measure of an angle when we know the measures of its components. This concept is essential in geometry and has many real-world applications.
Mastering the Angle Addition Postulate takes practice and patience, but with persistence and dedication, you can become proficient in applying this concept to solve problems in geometry and other areas of mathematics. Remember to start with simple angles, use real-world examples, create your own diagrams, practice with multi-step problems, and apply the postulate to other geometric concepts. With time and practice, you’ll become more confident in your ability to apply the Angle Addition Postulate and solve more complex problems in geometry.
Related Terms:
- Angle addition postulate worksheet answers
- Angle addition postulate worksheet pdf
- Angle Addition Postulate Worksheet Kuta
- Angle Addition Postulate PDF
- Angle Addition Postulate Notes



