7 Algebra Properties You Must Know

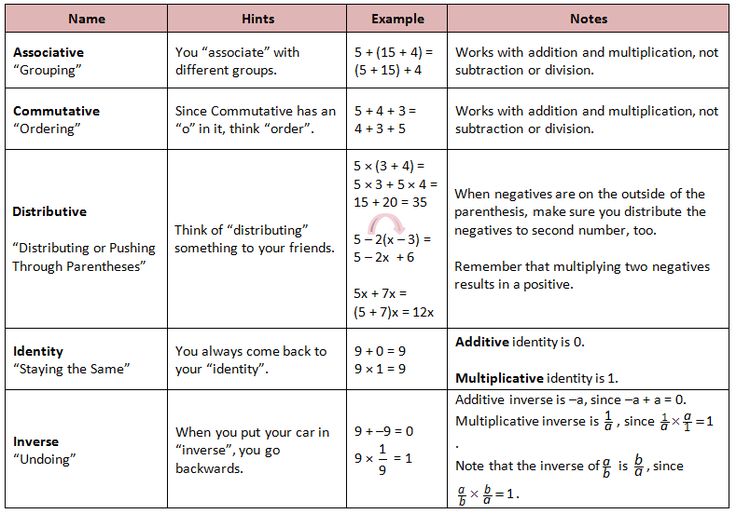
1. Commutative Property

The Commutative Property states that changing the order of numbers does not change the result in addition and multiplication operations. Here’s how it works:
- For addition: a + b = b + a
- For multiplication: a * b = b * a
By understanding this property, you can rearrange terms to make problems more manageable.
2. Associative Property

The Associative Property of algebra suggests that the way we group numbers or terms does not matter when adding or multiplying. It can be expressed as:
- For addition: (a + b) + c = a + (b + c)
- For multiplication: (a * b) * c = a * (b * c)
This property is particularly useful when you need to simplify complex expressions.
Example

Consider the sum: 2 + (3 + 4) = (2 + 3) + 4. Here, both expressions yield the same result, which is 9.
🔑 Note: The associative property does not hold true for subtraction or division, so be careful when these operations are involved.
3. Distributive Property

The Distributive Property combines addition and multiplication, allowing you to distribute one operation over another. It’s defined as:
- a(b + c) = ab + ac
- (a + b)c = ac + bc
It's a cornerstone for algebraic manipulation, allowing you to expand or factor expressions efficiently.
Example

If you have the expression 4(x + 3), you can use the distributive property to expand it to:
- 4 * x + 4 * 3 = 4x + 12
4. Identity Property

The Identity Property involves numbers that do not alter the value of other numbers when operated on:
- Addition identity: a + 0 = a, where 0 is the identity element for addition.
- Multiplication identity: a * 1 = a, where 1 is the identity element for multiplication.
These properties help in simplifying equations and understanding the basic structure of numbers.
5. Inverse Property

The Inverse Property relates to the existence of an element that, when combined with another element, will produce the identity element:
- Addition inverse: a + (-a) = 0
- Multiplication inverse (if a ≠ 0): a * (1/a) = 1
This property is crucial for solving equations by isolating the unknown.
6. Zero Property

The Zero Property has implications for both addition and multiplication:
- a + 0 = a
- a * 0 = 0
It's fundamental to understand how zero impacts algebraic expressions.
7. Property of Inequalities

Algebraic inequalities also have specific properties that are important for solving and manipulating them:
- Adding or subtracting the same number from both sides of an inequality does not change its direction.
- Multiplying or dividing both sides by a positive number does not change its direction.
- Multiplying or dividing both sides by a negative number flips the inequality sign.
Example

If we have the inequality 3x > 6 and we multiply both sides by -1, we get -3x > -6, which flips the sign to -3x < -6 when dividing by -1 again.
In summary, these seven algebraic properties are essential tools in your mathematical toolkit. They not only simplify calculations but also provide a deeper understanding of how numbers interact. Whether you're solving equations, inequalities, or just simplifying expressions, knowing these properties can make algebra less daunting and more logical. Mastery of these concepts will enhance your problem-solving skills, allowing you to approach algebraic challenges with confidence and precision.
Why is the commutative property important in algebra?
+
The commutative property allows for flexibility in rearranging terms, making algebraic manipulation and problem-solving much easier.
Can the associative property be used with subtraction and division?

+
No, the associative property does not hold for subtraction or division. The way these operations are grouped can change the result.
What is the main application of the distributive property?

+
The distributive property is crucial for expanding and factoring expressions, which is key to solving algebraic equations and simplifying terms.
How does understanding the properties of inequalities help in problem-solving?

+
Knowing these properties ensures that you can correctly manipulate inequalities to solve for unknowns, preventing mistakes in the process.
Is it necessary to memorize these properties?

+
Yes, having these properties at your fingertips will improve your speed and accuracy in algebraic operations and problem-solving.