5 Must-Know Algebra 2 Transformations for Better Grades

Algebra 2 is an exciting subject that builds upon your previous knowledge and introduces you to more complex mathematical concepts. One of the key areas where students often seek improvement is in understanding and applying transformations to functions. Transformations can significantly alter the graphs and properties of functions, making them appear different in shape, size, orientation, or location. Here are five must-know transformations that can help you secure better grades in Algebra 2.
Horizontal and Vertical Shifts
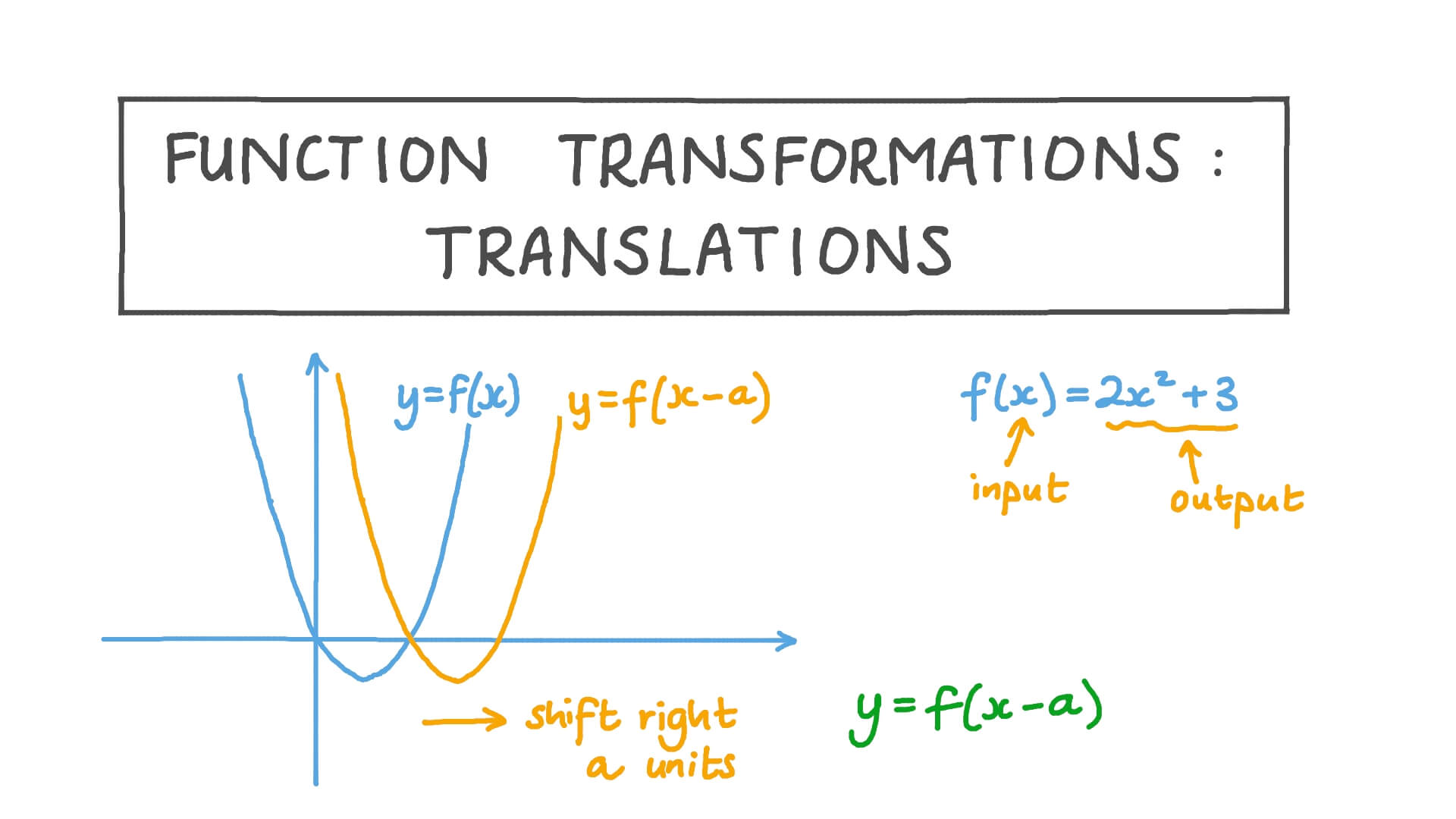
Transformations involving shifts are the most basic yet essential ones to master. When a function like f(x) is transformed to f(x) + c or f(x - c), it undergoes a vertical or horizontal shift respectively.
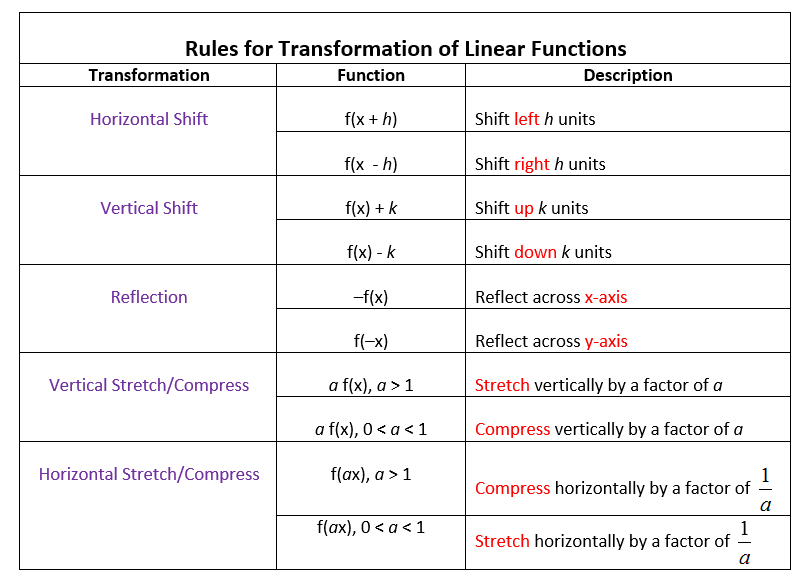
- Vertical Shifts:
- Upward shift by c units: f(x) + c
- Downward shift by c units: f(x) - c
- Horizontal Shifts:
- To the left by c units: f(x + c)
- To the right by c units: f(x - c)

Notes:
📌 Note: Remember, horizontal shifts operate inversely to what the equation suggests; adding inside the function shifts the graph to the left, while subtracting shifts it to the right.
Reflections

Reflections change the function's orientation, either across an axis or across the line y = x. These transformations are crucial for understanding symmetry:
- Reflection over the x-axis: -f(x)
- Reflection over the y-axis: f(-x)
- Reflection over the line y = x: Interchange x and y in the equation

Notes:

📍 Note: Reflecting over the y-axis or x-axis is straightforward, but reflecting over y = x requires you to find the inverse function.
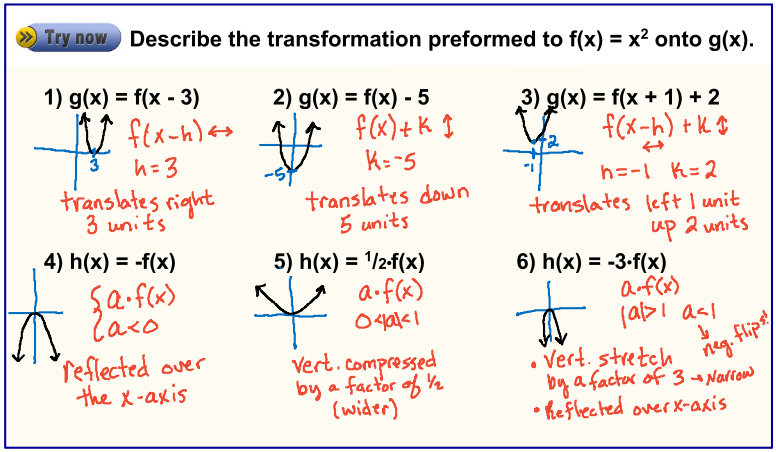
Vertical and Horizontal Stretches and Compressions

These transformations alter the function’s growth rate or speed along the axes:
- Vertical Stretch: af(x) where a > 1
- Vertical Compression: af(x) where 0 < a < 1
- Horizontal Stretch: f(x/b) where 0 < b < 1
- Horizontal Compression: f(x/b) where b > 1

Notes:
💡 Note: Vertical transformations affect the output values, whereas horizontal transformations affect the input values.
Multiple Transformations

Real-world problems often require the application of multiple transformations to a single function. Understanding how these interact with each other is key:
| Transformation Order | Equation |
|---|---|
| 1. Reflection | -f(x) |
| 2. Stretching or Compressing | af(x) or f(x/b) |
| 3. Horizontal Shifting | f(x - c) |
| 4. Vertical Shifting | f(x) + d |


Notes:

🚨 Note: When performing multiple transformations, the order matters as each transformation can affect the subsequent ones.
Modelling Real-Life Problems

These transformations are not just for textbook exercises but are instrumental in real-world applications:
- Environmental Science: Predicting changes in animal population growth
- Engineering: Modifying systems to optimize performance
- Economics: Modeling market trends

Notes:

🌍 Note: Real-life applications often involve adjusting parameters to fit observed data, which can be visualized through these transformations.
Transformations in Algebra 2 open the door to a deeper understanding of how functions work and how they can be manipulated to fit various scenarios. By mastering these transformations, you're not only ensuring better grades but also equipping yourself with powerful tools for analysis and problem-solving in real-world scenarios. Keep practicing these transformations, understand their effects on the graphs and properties of functions, and use them wisely in your next math examination or practical application. Your proficiency in these concepts will not only make algebra more engaging but will also pave the way for success in higher mathematics.
What is the difference between a vertical and a horizontal shift?

+
A vertical shift moves the entire graph of the function up or down by adding or subtracting from the output value, whereas a horizontal shift moves the graph left or right by adjusting the input value inside the function.
How do I know if a function has been stretched or compressed?

+
If a constant multiplied by f(x) is greater than 1, it causes a vertical stretch; if less than 1, a vertical compression. For horizontal transformations, the reciprocal of the constant applied to x affects the function: if less than 1, it stretches, if greater than 1, it compresses.
Why is it important to understand the order of transformations?
+
The order of transformations affects how each transformation impacts the function graph. For instance, shifting after reflecting changes the outcome compared to reflecting after shifting. Knowing the correct sequence ensures accurate manipulation of the function.
Can transformations be used in real-life scenarios?
+
Yes, transformations are incredibly useful for modeling real-life phenomena such as population dynamics, economic growth, or engineering optimizations, allowing us to predict outcomes and adjust parameters accordingly.
How do you reflect a function over y = x?

+
Reflecting over y = x means finding the function’s inverse by swapping the roles of x and y in the equation and then solving for the new y.