5 Steps to Master Absolute Value Equations in Algebra 2

In the world of algebra, particularly Algebra 2, understanding absolute value equations stands as a crucial step in mastering the intricacies of mathematical problem-solving. These equations, with their dual nature, can appear daunting to students at first. However, with the right approach, one can quickly unlock the patterns and techniques needed to conquer them. Let's explore the essential steps to mastering absolute value equations.
Understanding Absolute Value


The journey to mastering absolute value equations begins with a firm understanding of what absolute value represents. The absolute value of a number is the distance from that number to zero on the number line, always resulting in a non-negative value. Here’s what you need to know:
- Definition: |x| = x if x ≥ 0, and |x| = -x if x < 0.
- Visual Representation: The graph of the absolute value function, y = |x|, showcases a V-shaped curve opening upwards from the origin.
- Properties: Absolute value behaves differently with addition and multiplication; for example, |a + b| ≤ |a| + |b| (triangle inequality).
💡 Note: Absolute value functions can be solved graphically, but our focus here is on solving equations algebraically.
Step-by-Step Solution Process

Absolute value equations often hide two solutions within a single equation. Here’s how to dissect them:
- Isolate the Absolute Value Expression: Move all non-absolute terms to one side of the equation to isolate the absolute value. For example, |x + 2| - 4 = 3 becomes |x + 2| = 7.
- Set Up Two Equations: Since absolute value removes the sign, you’ll need to solve the equation for both positive and negative cases. From the previous example:
- x + 2 = 7
- x + 2 = -7
- Solve Each Equation: Solve both equations independently. Continuing the example:
- x = 5
- x = -9
- Check Your Solutions: Substitute your answers back into the original equation to ensure they are valid. Both x = 5 and x = -9 satisfy |x + 2| - 4 = 3.
- Refine Your Understanding: Practice with various forms of absolute value equations, such as |ax + b| = c or |ax + b| + |cx + d| = e, to solidify your grasp of the method.
🔎 Note: When solving absolute value equations, always consider whether there are extraneous solutions. Sometimes, due to hidden constraints within the equation, one of the solutions might not work.
Applications in Real-World Problems
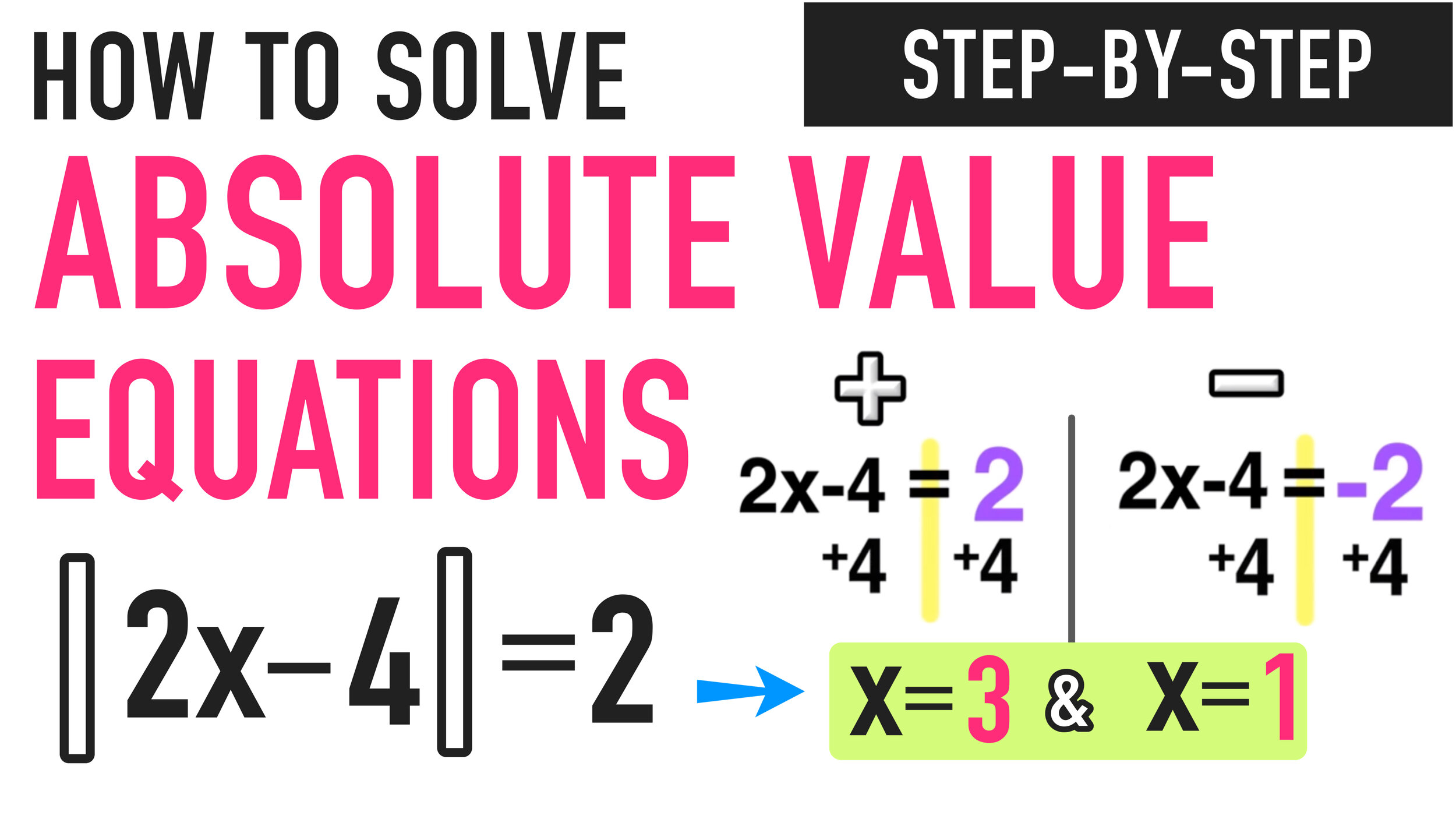
Absolute value equations have numerous applications in real life:
- Distance Problems: Calculating distances between points where direction is not significant.
- Error Analysis: To evaluate the magnitude of errors in data sets.
- Temperature Changes: Representing changes in temperature where the direction is unimportant.
🌡️ Note: Absolute value equations can be particularly useful in physics and engineering, where tolerance and precision are crucial.
Advanced Tips for Solving Absolute Value Equations

Beyond the basics, here are some advanced techniques and tips to enhance your problem-solving skills:
- Dealing with Multiple Absolute Values: If an equation involves multiple absolute values, break it down piece by piece.
- Inequalities: When working with absolute value inequalities, remember to consider both cases (greater than or equal to, and less than or equal to).
- Graphical Insights: Use graphing tools to visualize solutions and gain a better understanding of absolute value functions.
🧮 Note: Understanding how to manipulate absolute value algebraically opens up advanced problem-solving techniques in algebra and beyond.
Troubleshooting Common Mistakes

Here are some common pitfalls students encounter when solving absolute value equations:
- Neglecting Negative Solutions: Always solve for both positive and negative cases.
- Ignoring the Absolute Value: It’s easy to forget that the expression inside the absolute value can be both positive or negative.
- Forgetting to Check Solutions: Failing to verify solutions can lead to accepting extraneous solutions.
By following these steps and tips, you'll be well-equipped to tackle absolute value equations in Algebra 2. Mastering these equations not only enhances your algebraic proficiency but also prepares you for more complex mathematical problems in fields like calculus, engineering, and data science.
To sum up, the key to mastering absolute value equations lies in understanding the nature of absolute value, breaking down equations systematically, checking your solutions meticulously, and applying this knowledge to real-world scenarios. With practice and persistence, you'll find yourself confidently solving these equations, ready to conquer the more challenging aspects of algebra and beyond.
What is the difference between solving an absolute value equation and an absolute value inequality?

+
The main difference is in the solutions. For equations, you’ll have specific values for x that satisfy the equation. Inequalities, on the other hand, result in ranges of x values that satisfy the inequality. Also, with inequalities, you must consider cases where the expression inside the absolute value is greater than or less than a value, in addition to equal to.
Can an absolute value equation have no solutions?

+
Yes, if the value on the other side of the equation is negative, there will be no solution because an absolute value expression can’t equal a negative number. For example, |x| = -5 has no solutions.
How do absolute value equations relate to quadratic equations?

+
Solving absolute value equations often involves setting up two linear equations, similar to how solving quadratic equations involves finding roots. In some cases, absolute value equations can mimic the behavior of quadratic equations, especially when considering both positive and negative values of the expression inside the absolute value.
Why is it important to check the solutions in absolute value equations?

+
Checking solutions is crucial because absolute value equations can introduce extraneous solutions due to the removal of the absolute value. Also, the conditions inside the absolute value might limit the acceptable solutions, making verification necessary.