Algebra 2 Piecewise Functions: 5 Key Solutions

In the dynamic world of Algebra 2, piecewise functions stand out as a versatile tool for modeling complex scenarios where a single mathematical expression isn't sufficient. These functions, composed of multiple pieces defined over different intervals, provide a profound way to understand and analyze various real-world situations, from pricing structures to physical behaviors.
Understanding Piecewise Functions

Piecewise functions might seem intricate at first glance, but they are essentially functions built from simpler functions, each applicable to a specific segment of the domain. Here's what you need to know:
- Segments: Each segment of a piecewise function represents a piece, which can be linear, polynomial, or even another type of function.
- Intervals: These segments are defined over specific intervals, which can be expressed using inequalities or set notation.
- Endpoints: The endpoints of these intervals might be open or closed, affecting how we plot the function.
- Continuity: Not all piecewise functions are continuous, and some might have discontinuities where the pieces join or jump.
Solving Problems with Piecewise Functions

Here are five key solutions for understanding and solving problems involving piecewise functions:
1. Graphing
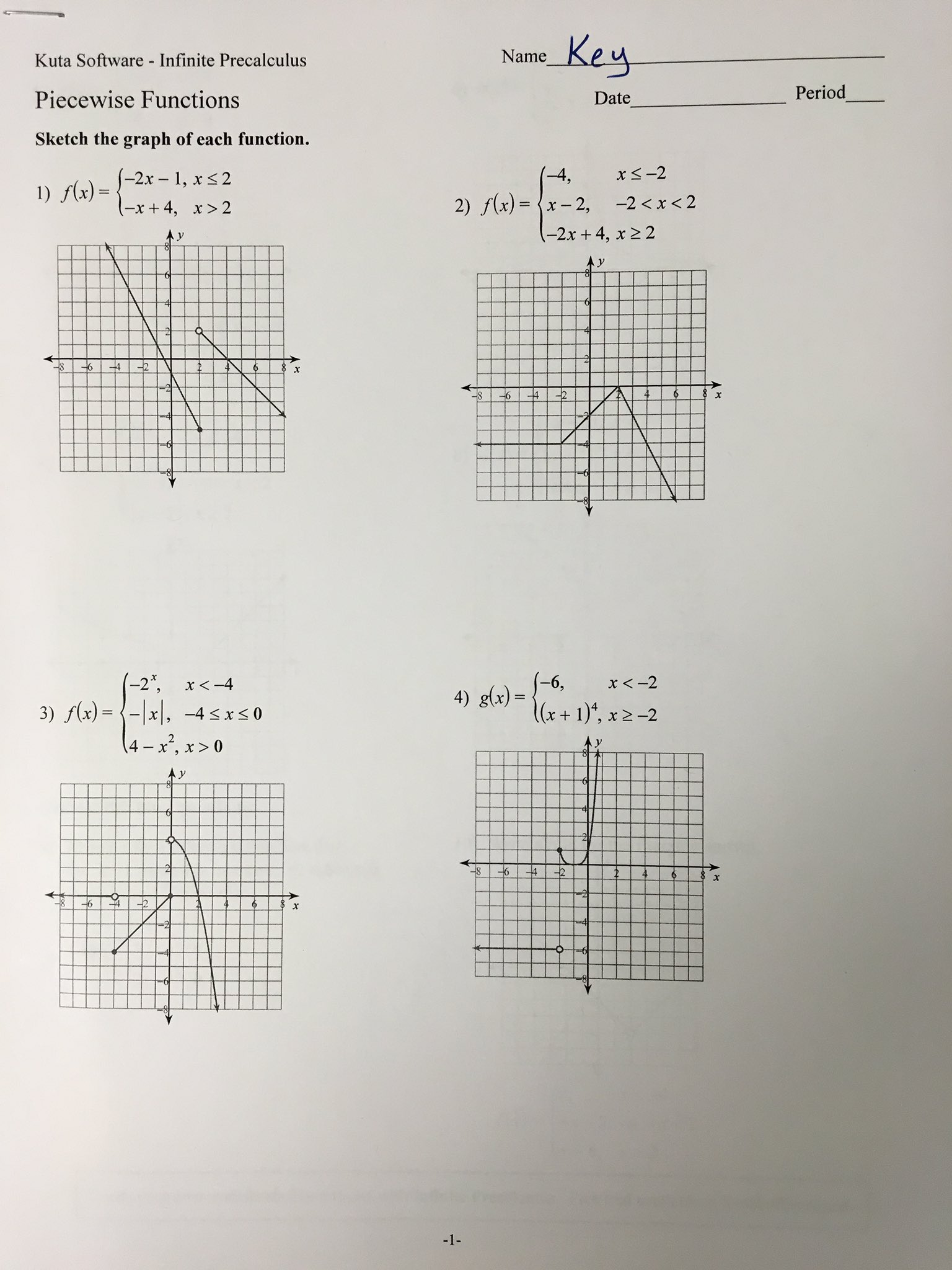
Graphing a piecewise function can reveal a lot about its behavior:
- Plot each segment on its respective domain, carefully considering open and closed endpoints.
- Use different colors or styles for each piece to distinguish them visually.
- Pay attention to any discontinuities, which might be jumps, removable, or infinite discontinuities.
Here's an example:

2. Evaluating a Piecewise Function

Evaluating a piecewise function for specific values involves:
- Determining which segment the value falls into.
- Applying the corresponding rule or formula for that segment.
- Verifying the correct piece for boundary values, considering open or closed intervals.
For example:
| Function | f(x) = \begin{cases} 2x, & \text{if } x \leq 0 \\ x^2, & \text{if } x > 0 \end{cases} |
|---|---|
| Evaluate at x = -2 | f(-2) = 2 \times (-2) = -4 |
| Evaluate at x = 3 | f(3) = 3^2 = 9 |

3. Continuity and Limits

Continuity of piecewise functions requires:
- Ensuring the segments align at their points of intersection or endpoints.
- Understanding the concept of one-sided limits to determine continuity at transition points.
🔍 Note: To check for continuity at a transition point, ensure that \lim_{{x \to a^-}} f(x) = \lim_{{x \to a^+}} f(x) = f(a).
4. Solving Equations and Inequalities
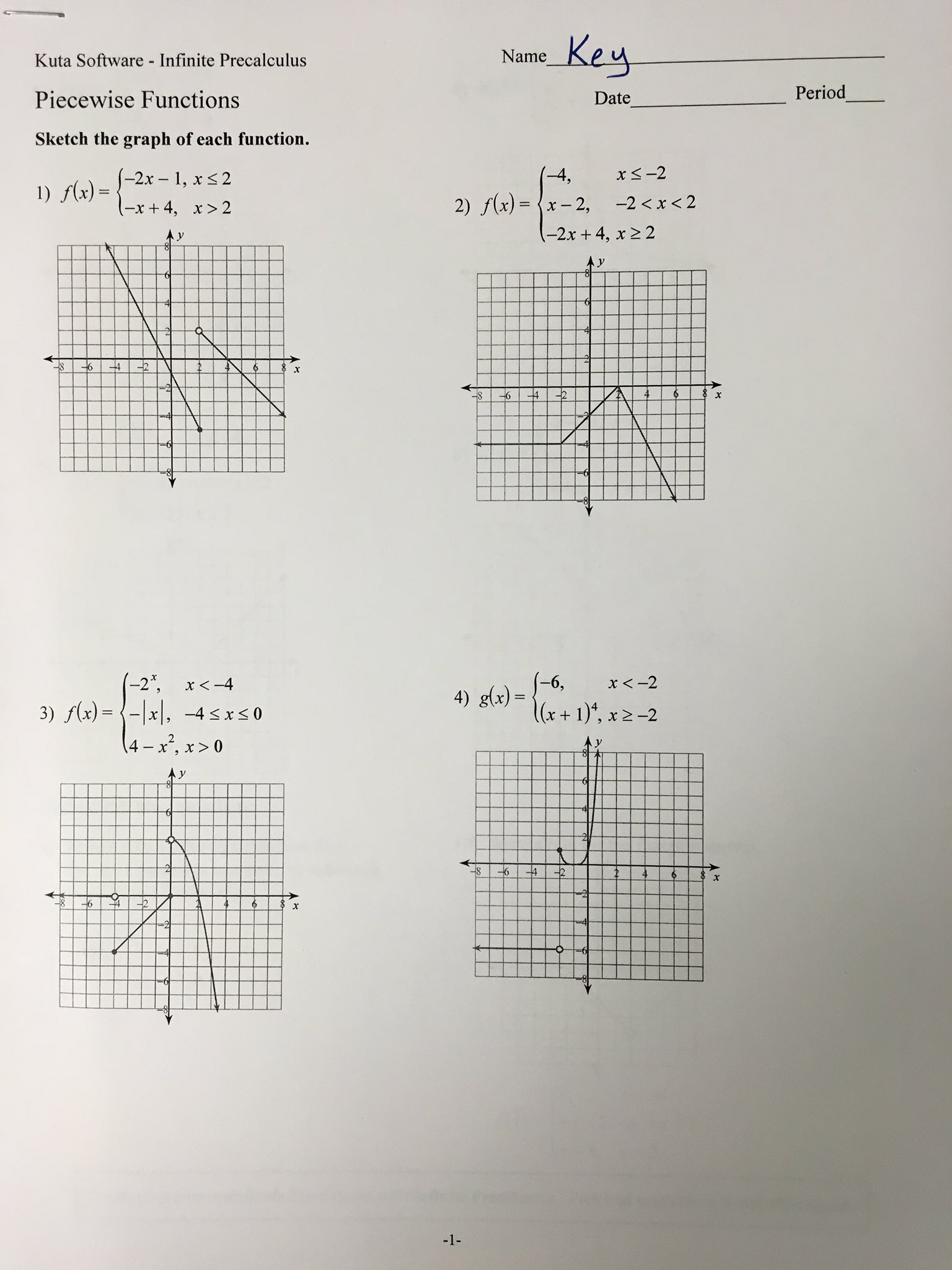
Here's how to approach solving equations or inequalities involving piecewise functions:
- Identify the piece of the function relevant to your variable's value.
- Solve for the variable within that piece, considering the domain restrictions.
- Check for solutions at the boundary points or transition points of the function.
5. Application in Real-World Problems

Piecewise functions shine in real-world scenarios:
- Pricing Models: Different rates apply at different usage levels or time periods.
- Physical Models: Changes in force or acceleration over time.
- Economics: Tax brackets, demand curves, or cost functions that change based on quantity produced or sold.
Mastering the Concepts

Algebra 2 piecewise functions not only challenge your understanding of functions but also enhance your analytical skills. Here are some tips for mastering these concepts:
- Practice plotting piecewise functions to visualize their behavior.
- Work through problems where you must evaluate, graph, and solve equations using piecewise functions.
- Apply these functions to real-world problems to see their relevance and utility.
By systematically approaching these functions, you can gain a deeper understanding of not just algebra, but also the logical structuring of various problem-solving scenarios. Piecewise functions are not merely mathematical constructs; they are tools for dissecting and understanding the complexity of the world around us.
What is the importance of intervals in piecewise functions?

+
Intervals define the domain for each piece of a piecewise function, ensuring that the function is appropriately applied over the correct range of values. This segmentation allows the function to model different behaviors at different inputs.
How do you determine if a piecewise function is continuous?

+
A piecewise function is continuous if the limit of the function as (x) approaches each transition point from both sides exists and equals the function’s value at that point. This means the function’s pieces must meet at their transition points without a gap or jump.
Can piecewise functions have discontinuities?

+
Yes, piecewise functions often exhibit discontinuities. These can be jump, removable, or infinite discontinuities depending on how the pieces of the function meet at their endpoints or transition points.