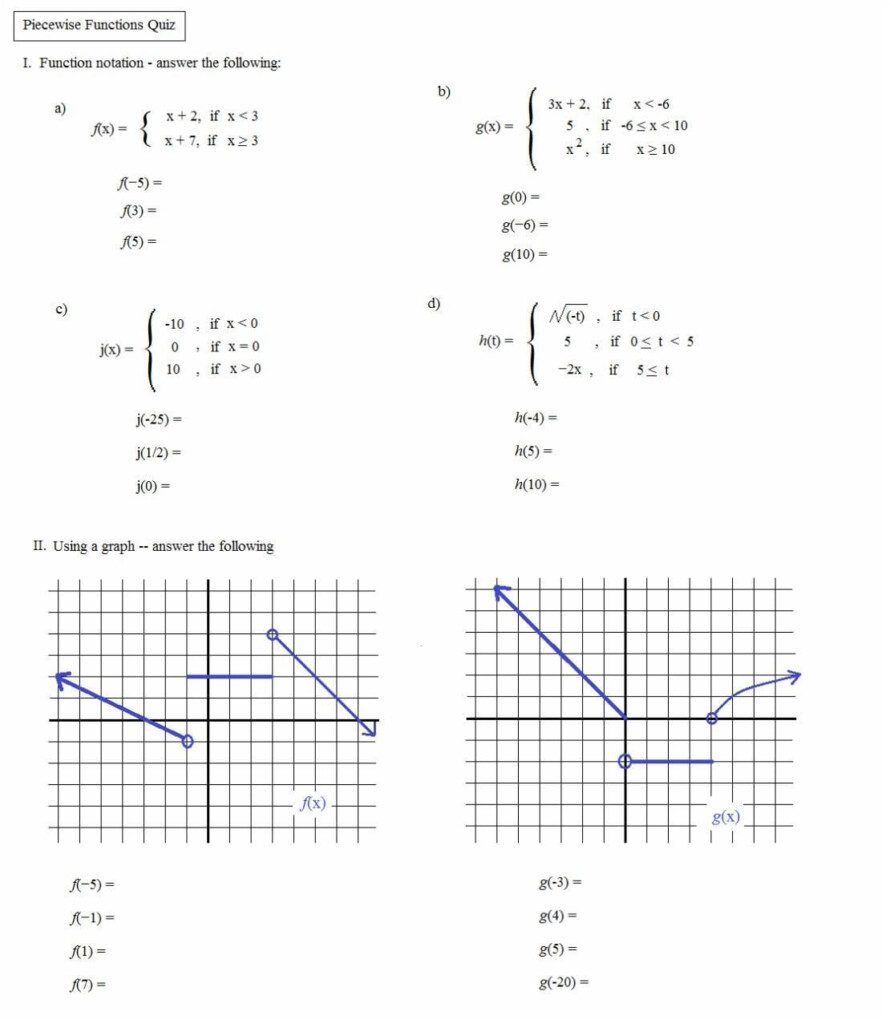
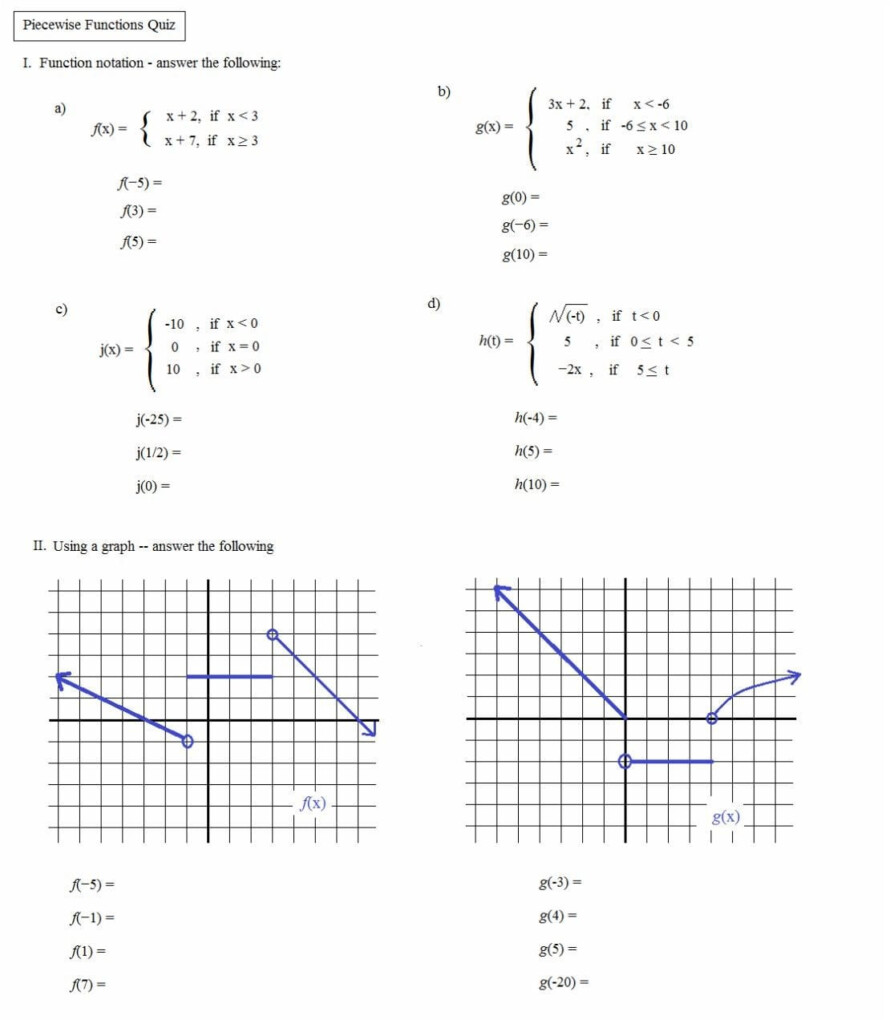
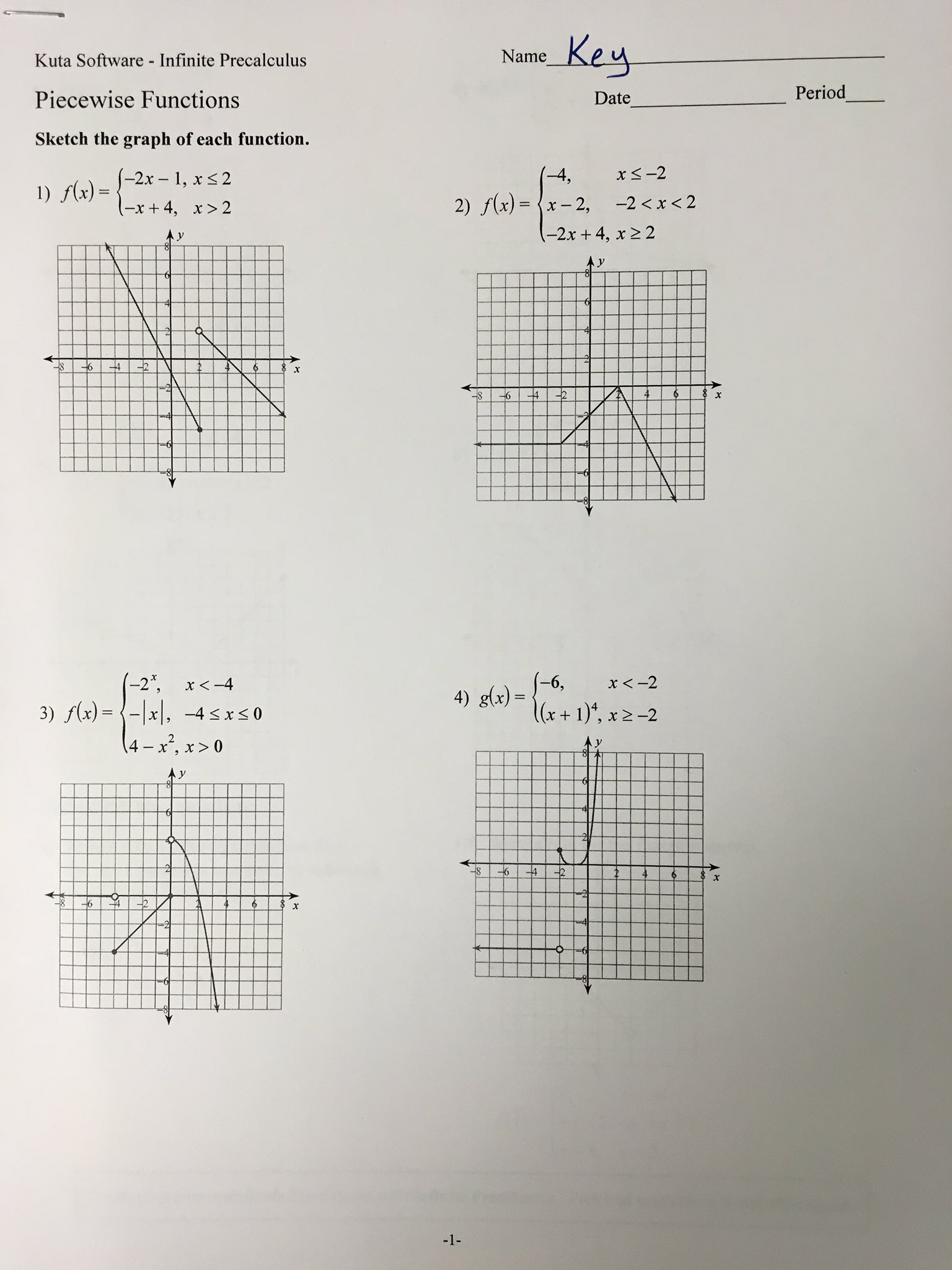
Algebra 2 Piecewise Functions Worksheet: Master Step-by-Step

In the realm of algebra, understanding and solving piecewise functions is a crucial skill. Piecewise functions are special functions that consist of multiple sub-functions, each defined over a specific interval or set of points. These functions can model complex, real-world scenarios where behavior changes abruptly at certain conditions or points. Today, we're diving deep into an Algebra 2 Piecewise Functions Worksheet, providing step-by-step guidance to master this topic.
What Are Piecewise Functions?

Imagine a function that behaves differently based on where you are on the x-axis. A piecewise function gives you a set of rules that apply for different segments of the x-axis:
- Each segment has its own rule or equation.
- The rules change at specific points called break points or boundary points.
- The function is defined by specifying each equation and its corresponding domain.
How to Solve Piecewise Functions?
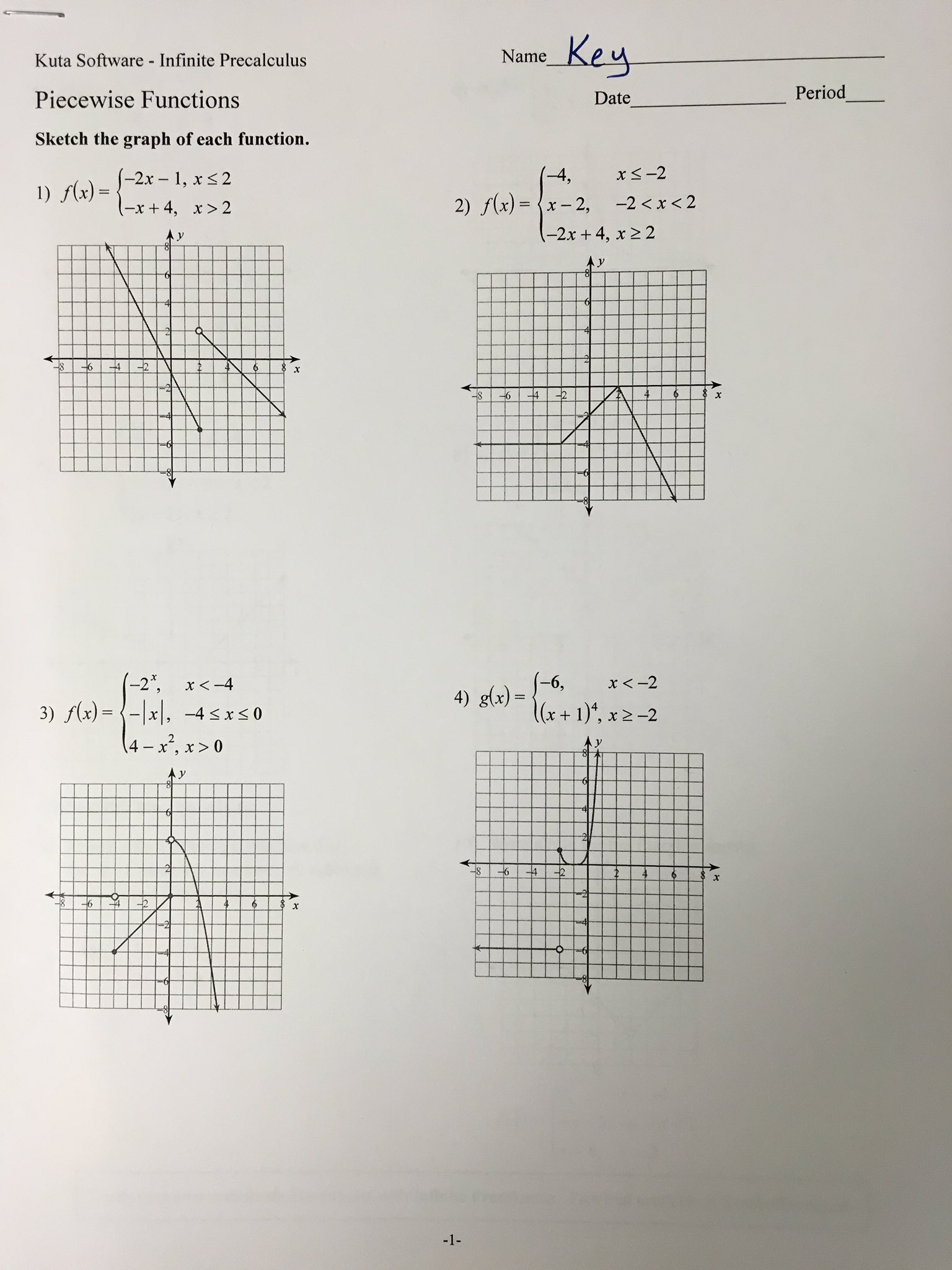
Here’s a step-by-step guide to solving problems involving piecewise functions:
Step 1: Identify the Intervals

- Look at the given piecewise function to understand where each segment applies. This is typically given as conditions like (x < a) or (a \leq x \leq b).
- Highlight these intervals for reference.
Step 2: Evaluate Each Segment
- Once you know the interval, use the appropriate equation to calculate the function value for the given x.
- Be careful to evaluate using the correct equation for the correct segment.
Step 3: Check Continuity and Discontinuity
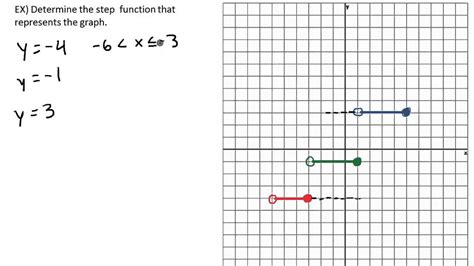
- Some piecewise functions have jump discontinuities where the value jumps suddenly at a boundary point.
- Others are continuous, where the function’s value at the boundary points from either side equals.
- Always check the behavior at these points.
Step 4: Sketch the Function
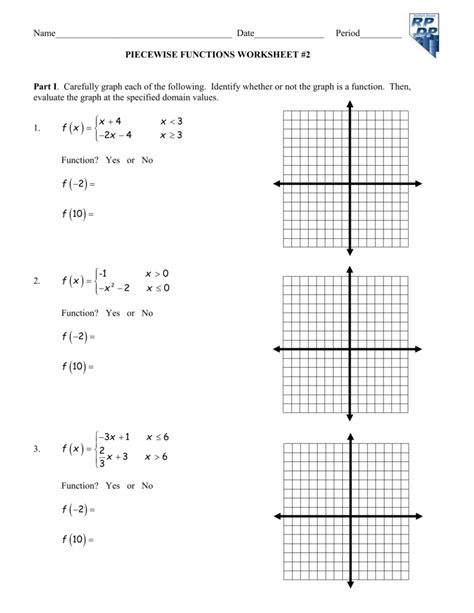
- Drawing the function helps visualize its behavior. Use a table of values if necessary:
| x | f(x) for x < 0 | f(x) for x ≥ 0 |
|---|---|---|
| -2 | -4 | NA |
| -1 | -1 | NA |
| 0 | 0 | 0 |
| 1 | NA | 1 |
| 2 | NA | 2 |
Step 5: Apply Domain and Range

- Understand the domain (the set of x-values) and range (the set of y-values) of the function.
📘 Note: In real-life problems, piecewise functions are used to model complex behavior where conditions dictate different outcomes, such as tax brackets or pricing plans.
Why Do We Need Piecewise Functions?

Piecewise functions allow us to model real-world problems where different rules apply under different conditions. Here’s why they’re important:
- Flexibility: They adapt to various scenarios with different rules for different regions.
- Accuracy: Allows for precise modeling of situations where behavior changes at specific points.
- Real-World Applications: Used in fields like economics, physics, engineering, and finance to model scenarios where conditions change abruptly.
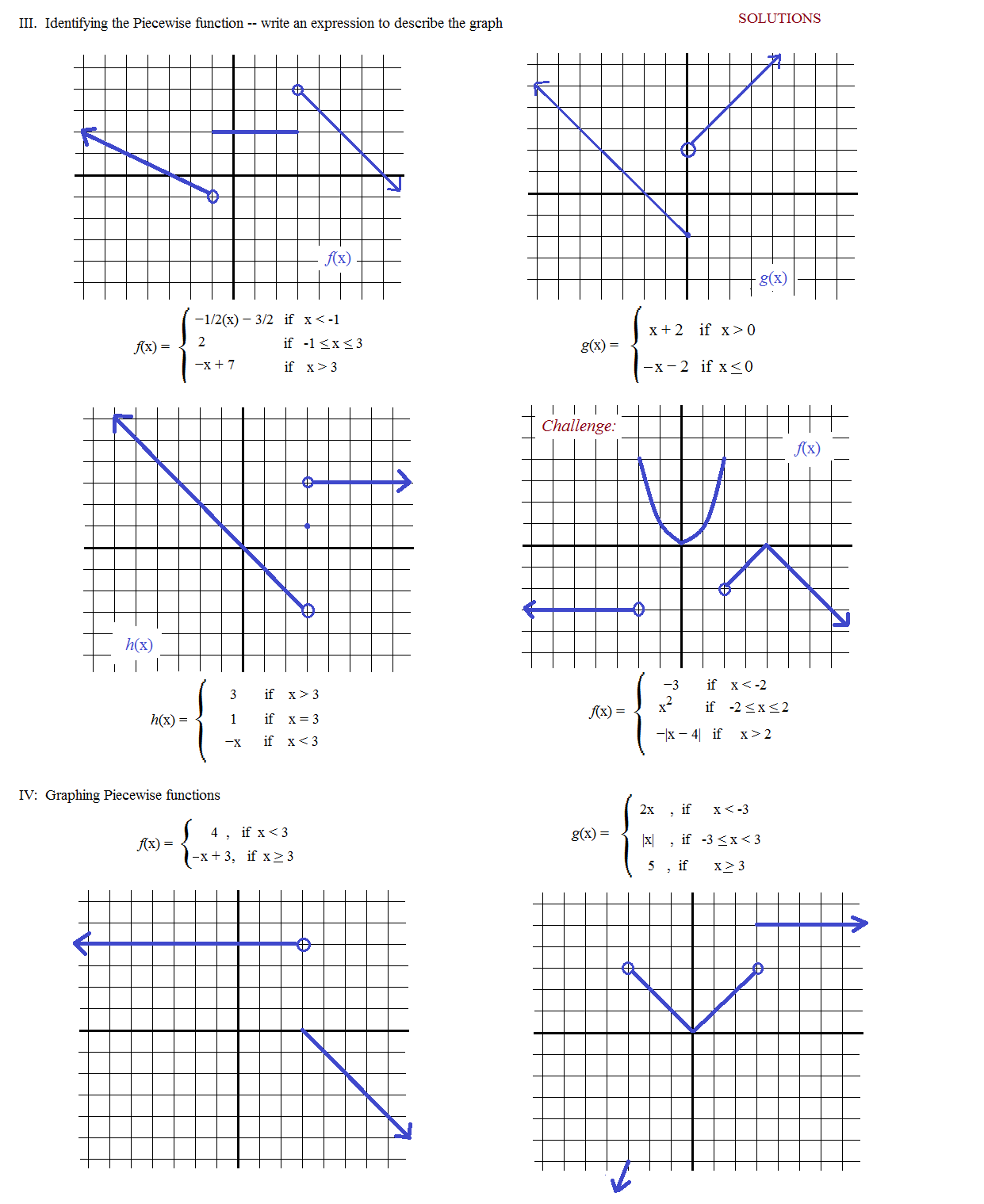
Sample Problems from the Worksheet

Let’s go through some common piecewise functions problems from your worksheet:
Problem 1: Evaluate and Graph
Given the function:
[ f(x) = \begin{cases} x + 2, & \text{if } x \leq 0 \ x - 1, & \text{if } x > 0 \end{cases} ]- Evaluate (f(x)) at (x = -2), (x = 0), and (x = 2).
- Graph the function, ensuring you indicate where the function is continuous or discontinuous.
Problem 2: Domain and Range

Consider the function:
[ g(x) = \begin{cases} 3x - 1, & \text{if } x \geq 1 \ 1, & \text{if } 0 \leq x < 1 \ x, & \text{if } x < 0 \end{cases} ]- Determine the domain and range of (g(x)).
- Discuss any possible discontinuities.
🔍 Note: When evaluating, always pay attention to boundary points as they might have values that are different when approached from different sides.
Tips for Mastering Piecewise Functions

- Understand the concept behind each segment’s application. What real-world scenario might it model?
- Practice sketching piecewise functions. Visualizing can help you remember the behavior of the function.
- Make sure to practice evaluating functions at boundary points to understand continuity and discontinuity.
As you navigate through your Algebra 2 Piecewise Functions Worksheet, keep these steps in mind, and practice consistently. Piecewise functions, once mastered, open up a world of practical problem-solving where you can model diverse and dynamic scenarios with mathematical precision. With every step, you're building a foundational understanding that will serve you well in higher mathematics and various applications in science and economics.
What is a piecewise function?

+
A piecewise function is a function that is defined using multiple sub-functions, each applied to a specific interval of the function’s domain. This allows for different behaviors or rules at different points.
How can I determine if a piecewise function is continuous?
+
To determine if a piecewise function is continuous, evaluate the function at its boundary points from both sides. If the value at the boundary point from the left side equals the value from the right side, the function is continuous at that point. If not, there is a discontinuity.
Can piecewise functions have any number of segments?

+
Yes, piecewise functions can have any number of segments. However, the function must be defined clearly for all values in its domain, ensuring that every x-value maps to exactly one y-value.


