Algebra 2 Vertex Form Mastery Worksheet Guide

Welcome to our guide on mastering the vertex form of quadratic equations, a topic that is often pivotal in Algebra II. This post aims to clarify the concepts, offer practical applications, and provide a step-by-step guide to help you excel in your algebra studies.
The Vertex Form of a Quadratic Equation

In algebra, quadratic equations can be expressed in various forms, but the vertex form is especially useful when analyzing the graph of a parabola. The general vertex form of a quadratic equation is:
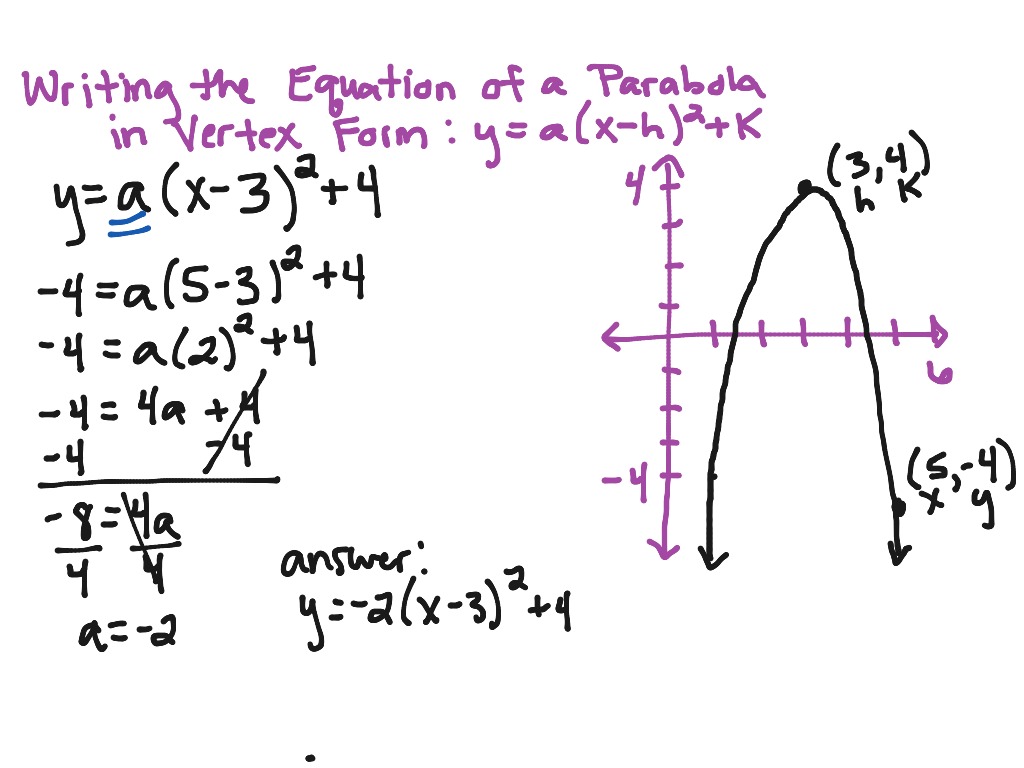
y = a(x - h)2 + k
- a: The a coefficient affects the direction of the parabola and how it stretches or compresses.
- (h, k): This is the vertex point where the parabola reaches its maximum or minimum value.
Why Use the Vertex Form?

Understanding the vertex form has several practical advantages:
- Easy Vertex Identification: The vertex (h, k) is directly read from the equation.
- Direction and Shape of Parabola: The sign of a dictates whether the parabola opens upwards or downwards, and its magnitude reflects how "skinny" or "wide" the parabola is.
- Finding Minimum or Maximum Values: The vertex gives us the y-value of the highest or lowest point, crucial in optimization problems.
Steps to Convert a Quadratic Equation to Vertex Form

Here’s a step-by-step guide to converting a standard form quadratic equation y = ax2 + bx + c to vertex form:
- Complete the square:
- Isolate the x-terms:
y = ax2 + bx + cbecomesy - c = ax2 + bx. - Factor a out of the x-terms:
y - c = a(x2 + (b/a)x). - Add and subtract
(b/2a)2inside the parentheses:y - c = a[(x + (b/2a))2 - (b/2a)2]. - Distribute a back through the parentheses:
y - c = a(x + (b/2a))2 - ab2/4a2. - Add c back to both sides:
y = a(x + (b/2a))2 - ab2/4a2 + c.
- Isolate the x-terms:
- Simplify: Group the constant terms to identify the vertex form clearly.
🧮 Note: Remember to take care with the signs and coefficients when completing the square, especially when dealing with negative values for a or b.
Application of Vertex Form in Real-World Problems

Let's delve into how vertex form can be applied to real-world scenarios:
- Projectile Motion: Determine the time a projectile is in the air and its maximum height.
- Economics: Find the optimal amount of production to maximize profits or minimize costs.
- Engineering: Analyze stress points in beams or the efficiency of a solar panel based on its positioning.
Practical Exercises with Solutions

Below is a table with exercises to practice transforming standard form equations into vertex form:
| Standard Form | Step-by-Step to Vertex Form | Vertex Form |
|---|---|---|
y = x2 + 6x + 7 |
1. y - 7 = x2 + 6x2. y - 7 = (x + 3)2 - 93. y = (x + 3)2 - 2 |
y = (x + 3)2 - 2 |
y = -2x2 + 8x - 7 |
1. y + 7 = -2(x2 - 4x)2. y + 7 = -2((x - 2)2 - 4)3. y = -2(x - 2)2 + 1 |
y = -2(x - 2)2 + 1 |

Summing Up Key Points

In this guide, we've delved into the intricacies of the vertex form of quadratic equations, offering you a robust understanding that can be applied to both academic and real-world problems. By mastering how to convert standard quadratic equations to vertex form, you can unlock a deeper understanding of parabolas, solve optimization problems, and make informed decisions in various contexts. We've walked through the conversion steps, provided practical examples, and highlighted real-life applications. Armed with this knowledge, you're well on your way to becoming an algebra virtuoso, ready to tackle more complex problems with confidence.
What is the vertex form useful for?

+
The vertex form is particularly useful for identifying the vertex of a parabola, which is crucial for understanding its maximum or minimum value, and it provides an intuitive way to analyze the parabola’s direction and shape.
Why might I need to convert from standard form to vertex form?
+
Converting helps you find the vertex easily, which is essential for solving real-world problems like maximizing profits or determining optimal conditions.
How does the value of ‘a’ in vertex form affect the parabola?

+
The sign of ‘a’ determines if the parabola opens upwards (positive) or downwards (negative), while its absolute value indicates how wide or narrow the parabola is.



