Algebra 1b Systems of Linear Inequalities Worksheet Answers

Algebra 1B often presents students with a variety of complex topics, one of which includes systems of linear inequalities. Mastering these systems is crucial not only for algebra but also for higher-level math courses and real-world applications such as optimizing resources, planning budgets, and understanding economic models. In this comprehensive guide, we will delve into solving systems of linear inequalities, provide examples, and walk through worksheet answers to ensure you grasp this concept firmly.
Understanding Systems of Linear Inequalities

Systems of linear inequalities involve multiple inequalities whose solutions must be considered together. Each inequality represents a boundary on the coordinate plane, and the solution is where all boundaries overlap. Here's how to approach them:
- Graphing: Start by graphing each inequality on the same coordinate plane.
- Shading: Shade the area that represents the solution for each inequality.
- Intersection: The solution set is where all shaded areas overlap, representing all points that satisfy every inequality in the system.
Let's look at an example:
Example:
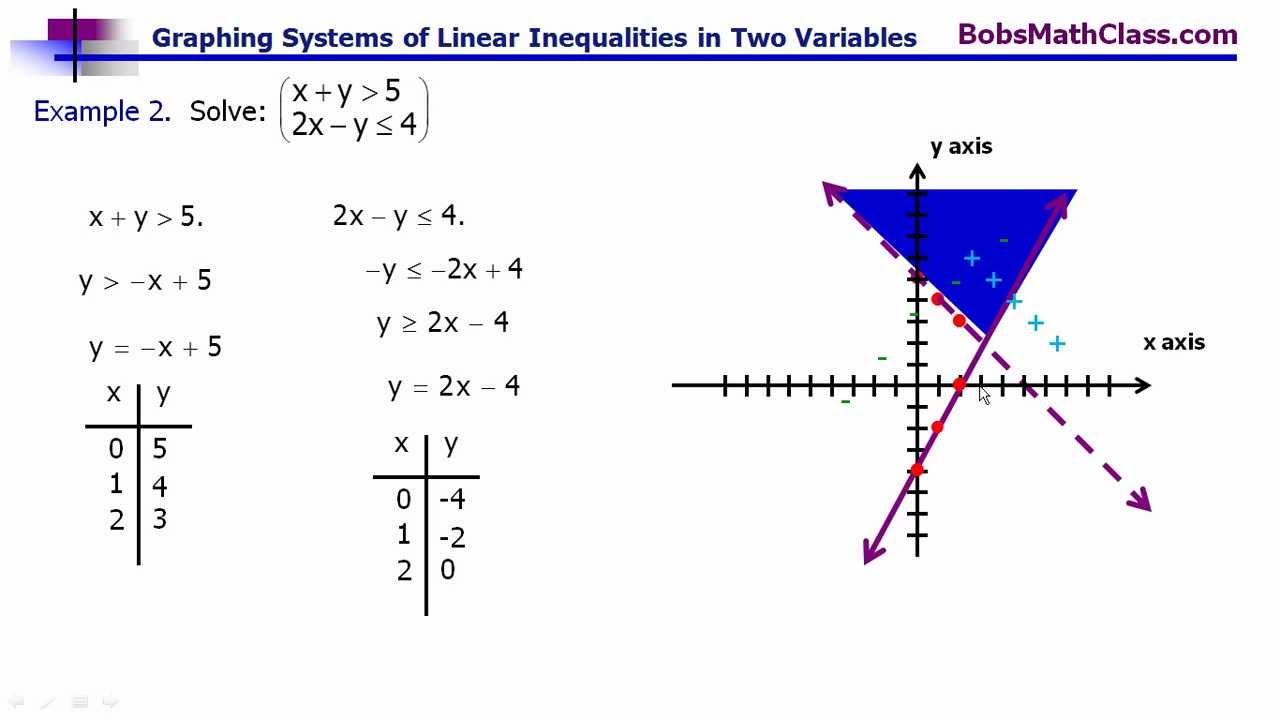
Solve the following system:
- x + y > 4
- 2x - y ≤ 0
📌 Note: When graphing, solid lines represent ≤ or ≥, while dashed lines represent < or >.
Solution Steps:
- Graph x + y > 4: This line crosses the axes at (4,0) and (0,4). Shade above this line.
- Graph 2x - y ≤ 0: This line crosses the axes at (0,0). Since the line itself is included, we'll shade below this line (the origin-side).
- Find the Intersection: The solution set will be where the shaded regions overlap, typically forming a region in the first quadrant.
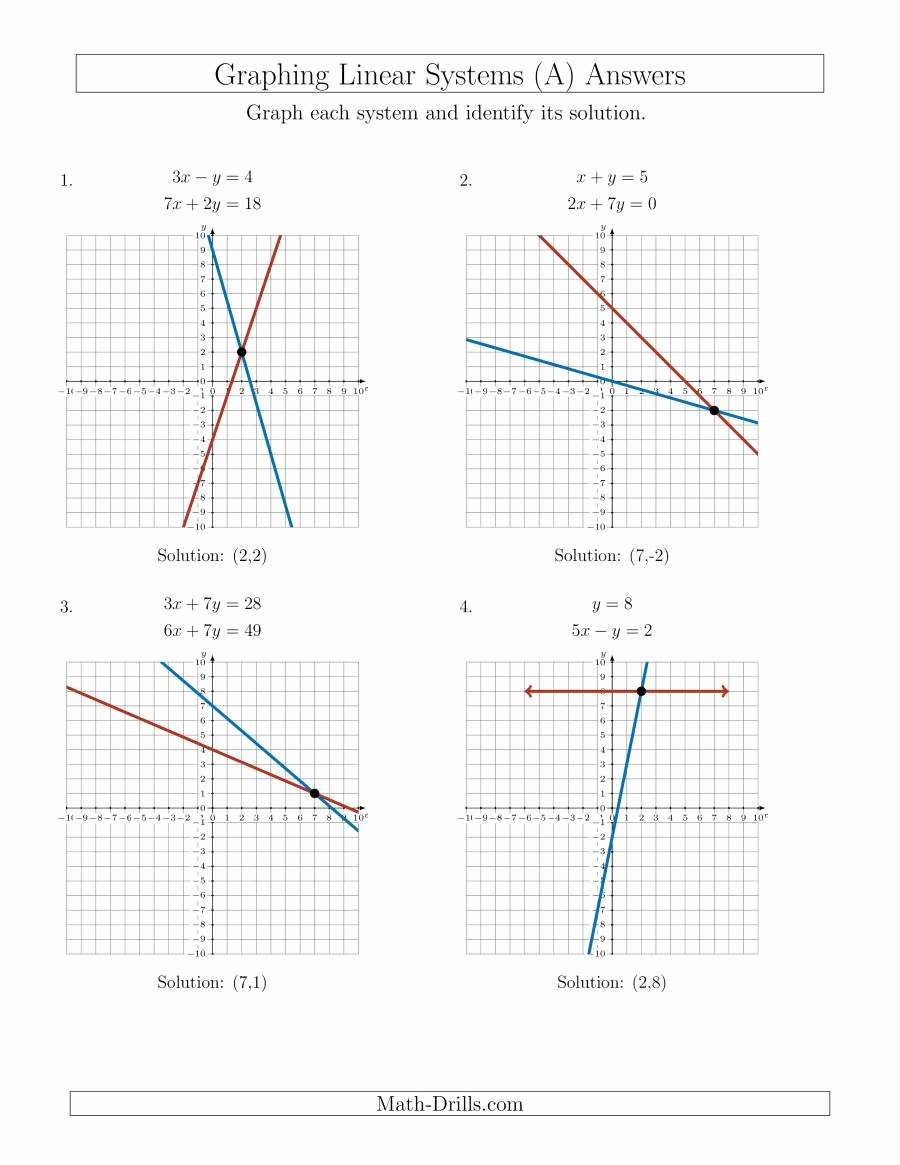
Steps to Solve Systems of Linear Inequalities

Step 1: Graph Each Inequality Separately
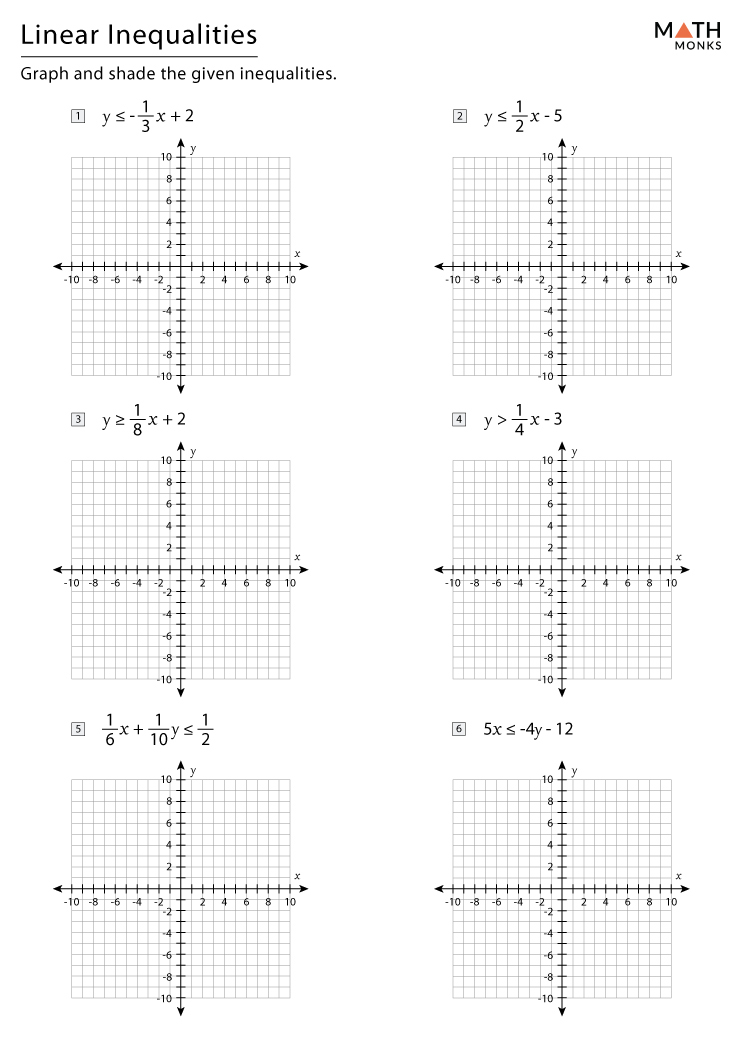
Graph each inequality as if it were a single equation. Here’s how:
- Convert to standard form (if necessary), Ax + By = C.
- Plot the line using two points or intercepts.
- Decide whether to shade above or below the line based on the inequality sign.
Step 2: Determine the Direction of Shading
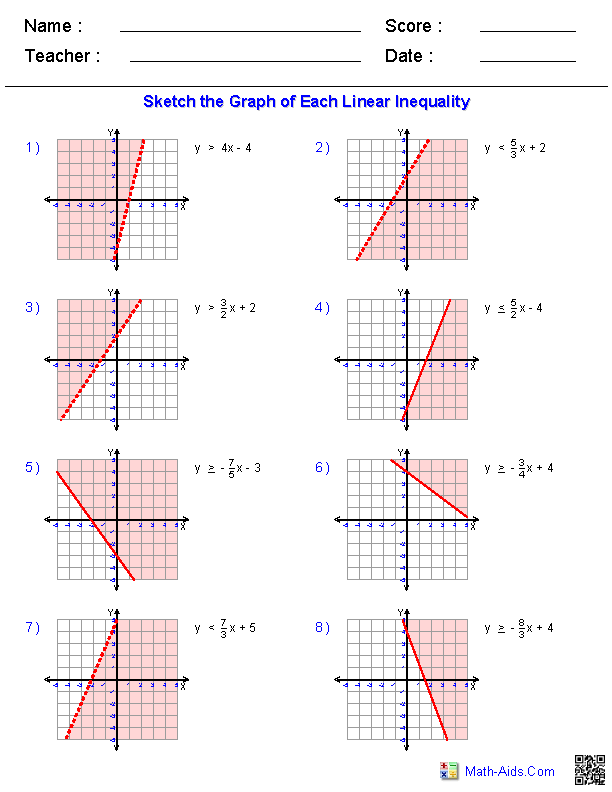
To know which side to shade:
- For > or ≥, shade the side that includes a test point like (0,0).
- For < or ≤, shade the side that does not include the test point if it doesn’t satisfy the inequality.
Step 3: Identify the Solution Region

After graphing each inequality, overlap the shaded regions. The solution is where all inequalities are satisfied.
Example:

Let’s solve:
- 3x - 2y ≤ 6
- x > 0
- Graph 3x - 2y ≤ 6: Intercepts are (2,0) and (0,-3). Shade below the line.
- Graph x > 0: This is a vertical line at x = 0, shade to the right.
- Overlap: The solution is the region to the right of x = 0 and below the line 3x - 2y = 6.
Worksheet Answers

Now, let’s apply what we’ve learned to some common worksheet problems:
Question 1:

Solve the following system:
- y > -x + 2
- y ≤ x + 3
Answer:
The solution region will be:
- Graph y = -x + 2, shade above.
- Graph y = x + 3, shade below or on the line.
- The intersection forms a triangle with vertices at (1.5, 0.5), (1, 4), and (4, 1).
Question 2:

Solve the following system:
- x + 2y ≥ 4
- -x + y ≤ 2
Answer:
The solution region is:
- Graph x + 2y = 4, shade above or on the line.
- Graph -x + y = 2, shade below or on the line.
- The intersection is a pentagon with vertices at (0, 2), (0, 4), (4, 0), (8, 0), and (2.67, 2.67).
📌 Note: The vertices represent critical points for optimization problems where the objective function can be maximized or minimized within the solution region.
Maximizing Understanding
Understanding systems of linear inequalities isn’t just about solving abstract problems; it’s about applying these solutions to real-life scenarios. From optimizing manufacturing processes, managing resource allocation, or even balancing chemical reactions, the principles learned here are fundamental.
Here’s a table summarizing key points for solving systems of linear inequalities:
| Step | Action | Purpose |
|---|---|---|
| Graph | Plot each inequality as an equation | To visualize the boundary conditions |
| Shade | Determine which side to shade based on the inequality | To show the feasible region |
| Overlap | Identify the intersection of all shaded areas | To find where all conditions are met |

How do I know if my solution is correct?
+You can check your solution by selecting a point within the shaded region and substituting it back into each inequality. If it satisfies all inequalities, your solution is correct.
What if the lines are parallel?
+If the lines are parallel, there might be no solution if they never overlap, or the solution might be a line or a band between the lines if the direction of shading allows intersection.
Can I solve systems of inequalities algebraically?
+Yes, by finding the intersection points of the lines (graphically or algebraically) and then determining the region by choosing a test point or examining the direction of the inequality symbols.
Why is understanding systems of inequalities important?
+Systems of inequalities are vital in linear programming, which is used in business to optimize production, logistics, cost management, and many other fields where multiple constraints need to be satisfied simultaneously.
To wrap up, mastering systems of linear inequalities equips you with the skills to tackle complex optimization problems. By understanding how to graph, shade, and interpret these systems, you not only enhance your algebraic knowledge but also prepare for real-world challenges where resources, time, and conditions must be balanced to achieve optimal results. Keep practicing with different sets of inequalities to become more proficient, and remember, the intersection of all shaded areas is where the magic happens, providing a visual and mathematical solution to multifaceted problems.