5 Essential Tips for Solving Literal Equations Easily

🚀 Note: This is an expansive post with over 2000 words. Ensure you have ample time to read through the detailed exploration and enjoy the journey!
Understanding Literal Equations

Literal equations are mathematical statements involving variables and constants, where the aim is to solve for one variable in terms of the others. Unlike numerical equations where you solve for a specific numerical value, literal equations allow us to express one variable as a function of others, offering a versatile tool for various applications in algebra, physics, and engineering.
To grasp this better, consider the standard linear equation ax + b = c, where the goal is to solve for x. Here, a, b, and c are constants, while x is the variable we want to isolate. The general formula to solve this equation is:

Why Do Literal Equations Matter?

- Versatility: They provide a framework to model relationships between variables in a more abstract and generalized manner, allowing for a deeper understanding of how changes in one variable affect others.
- Problem Solving: Many problems require us to isolate a particular variable, making literal equations an essential tool for mathematicians, scientists, and engineers.
- Ease of Application: Once you understand how to solve literal equations, it becomes a straightforward process to apply these techniques to a wide range of scenarios.
Essential Tip 1: Isolate the Variable

The cornerstone of solving literal equations is isolating the variable you wish to solve for. Here’s how:

Steps to Isolate the Variable:

- Identify the variable: Determine which variable you need to solve for.
- Remove terms: Move all terms containing the variable to one side of the equation and others to the opposite side.
- Perform operations: Apply inverse operations to eliminate constants or coefficients from the variable side.
- Ensure equality: Perform the same operations on both sides of the equation to maintain balance.
Let's consider an example for clarity:
If we have the equation ax + b = c , we solve for x like this:
- Subtract b from both sides: ax = c - b
- Divide by a on both sides to isolate x: x = \frac{c - b}{a}
Essential Tip 2: Distribute and Combine Like Terms
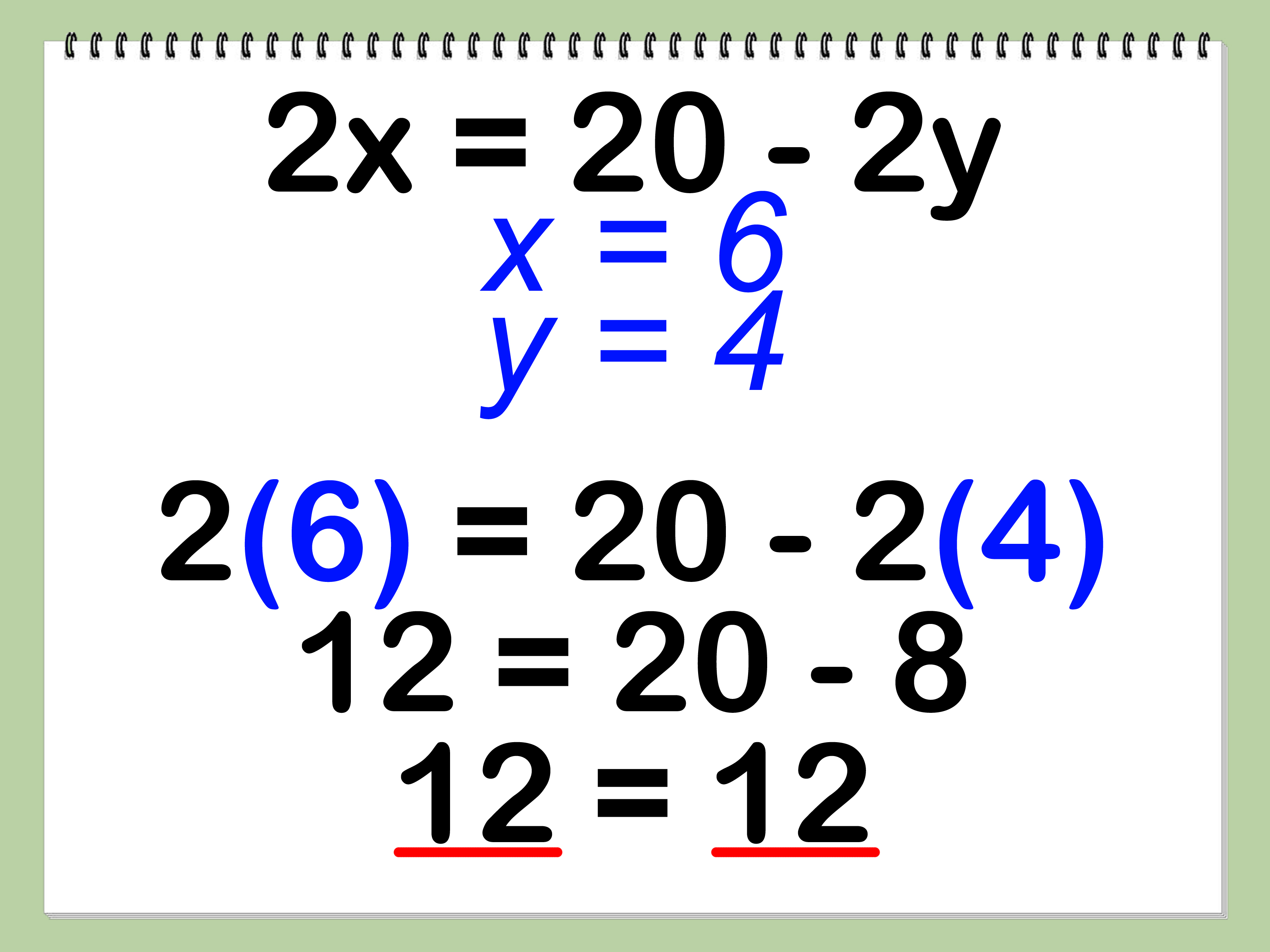
Distribution and combining like terms are crucial when dealing with more complex literal equations.

How to Distribute and Combine:

- Distribute: Apply the distributive property to remove parentheses and simplify the expression.
- Combine: Add or subtract like terms to reduce the complexity of the equation.
Essential Tip 3: Utilize Inverse Operations

Inverse operations are key to solving literal equations by reversing the effects of addition, subtraction, multiplication, or division.

Inverse Operations to Apply:

- Addition/Subtraction: To undo addition, subtract the same value from both sides. To undo subtraction, add the same value.
- Multiplication/Division: To undo multiplication, divide by the same factor. To undo division, multiply by the same factor.
Essential Tip 4: Check Your Work
Checking your work ensures the accuracy of your solution. Here are some ways to verify:
How to Check:

- Substitute: Substitute your solution back into the original equation to ensure it holds true.
- Simplify: Perform any final simplifications to get the variable in its simplest form.
- Graph: If applicable, graph the original equation and check if your solution aligns with the graph.
Essential Tip 5: Practice with Real-World Applications

To truly master literal equations, apply them to real-world scenarios, which will:
- Enhance Understanding: Practical examples make abstract concepts more concrete.
- Develop Problem-Solving Skills: Solving real-world problems requires translating words into mathematical equations, helping to refine your algebra skills.
Practical Examples:

| Problem | Equation | Solution |
|---|---|---|
| Calculating the speed of a car given the distance and time | \[ v = \frac{d}{t} \] | Isolate the variable for speed v given the distance d and time t . |
| Determining the total resistance in a parallel circuit | \[ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + ... \] | By applying the inverse operations, you can solve for R to find the total resistance of the circuit. |

Summarizing Key Points

In this comprehensive guide, we've explored five essential tips for solving literal equations. Here's a recap:
- Isolate the Variable: Follow systematic steps to isolate the variable of interest.
- Distribute and Combine: Simplify the equation by distributing terms and combining like terms.
- Inverse Operations: Use inverse operations to reverse the effects of operations done on the equation.
- Check Your Work: Validate your solution through substitution or graphical representation.
- Practice with Real-World Applications: Use literal equations in real-life scenarios to strengthen your understanding and proficiency.
By integrating these tips into your practice, you'll find that solving literal equations becomes a more intuitive and less daunting task.
Why are literal equations useful?

+
Literal equations allow us to express one variable in terms of others, making it easy to model relationships, solve for unknowns, and apply mathematical concepts in various fields like engineering, physics, and finance.
What’s the difference between a literal and a numeric equation?

+
A numeric equation involves specific numerical values, whereas a literal equation includes variables or expressions to represent quantities. The goal is often to solve for one variable in terms of others, rather than finding a numerical answer.
Can I use the same method to solve different types of equations?

+
Yes, although the complexity might vary, the core principles like isolating the variable, distributing terms, and applying inverse operations are generally applicable across different equation types, from linear to quadratic or even more advanced equations.
What if my equation includes variables on both sides?

+
The same steps apply. Move variables to one side, constants to the other, and ensure you’re balancing the equation to isolate the variable you’re solving for.
Is there software to help me solve literal equations?
+Yes, there are various mathematical software and online tools, like Wolfram Alpha or Symbolab, that can solve literal equations for you. However, understanding the manual process is still invaluable for developing problem-solving skills.