Algebra 1 Compound Inequalities Worksheet Answers Revealed

When it comes to mastering Algebra 1, compound inequalities are an essential concept to grasp. These types of inequalities can be quite intimidating at first, but with practice and understanding, students can master solving and interpreting them. This post will dive deep into compound inequalities, providing examples, solutions, and some key tips to ensure you excel in this area of algebra.
Understanding Compound Inequalities

Compound inequalities combine two or more inequalities together with AND or OR. Here's a quick overview:
- AND Inequalities: Both conditions must be true. They are often written with the same variable in between two inequalities.
- OR Inequalities: At least one of the conditions must be true. These are often separated by the word OR.
AND Inequalities

Let's look at an example:

In this case, we're solving the compound inequality:
-3 < x + 2 < 4
The steps to solve this are:
- Subtract 2 from all parts of the inequality:
- This means that x must be greater than -5 and less than 2. You can represent this solution on a number line with open circles at -5 and 2, and shading between them.
-3 - 2 < x + 2 - 2 < 4 - 2
Which simplifies to:
-5 < x < 2
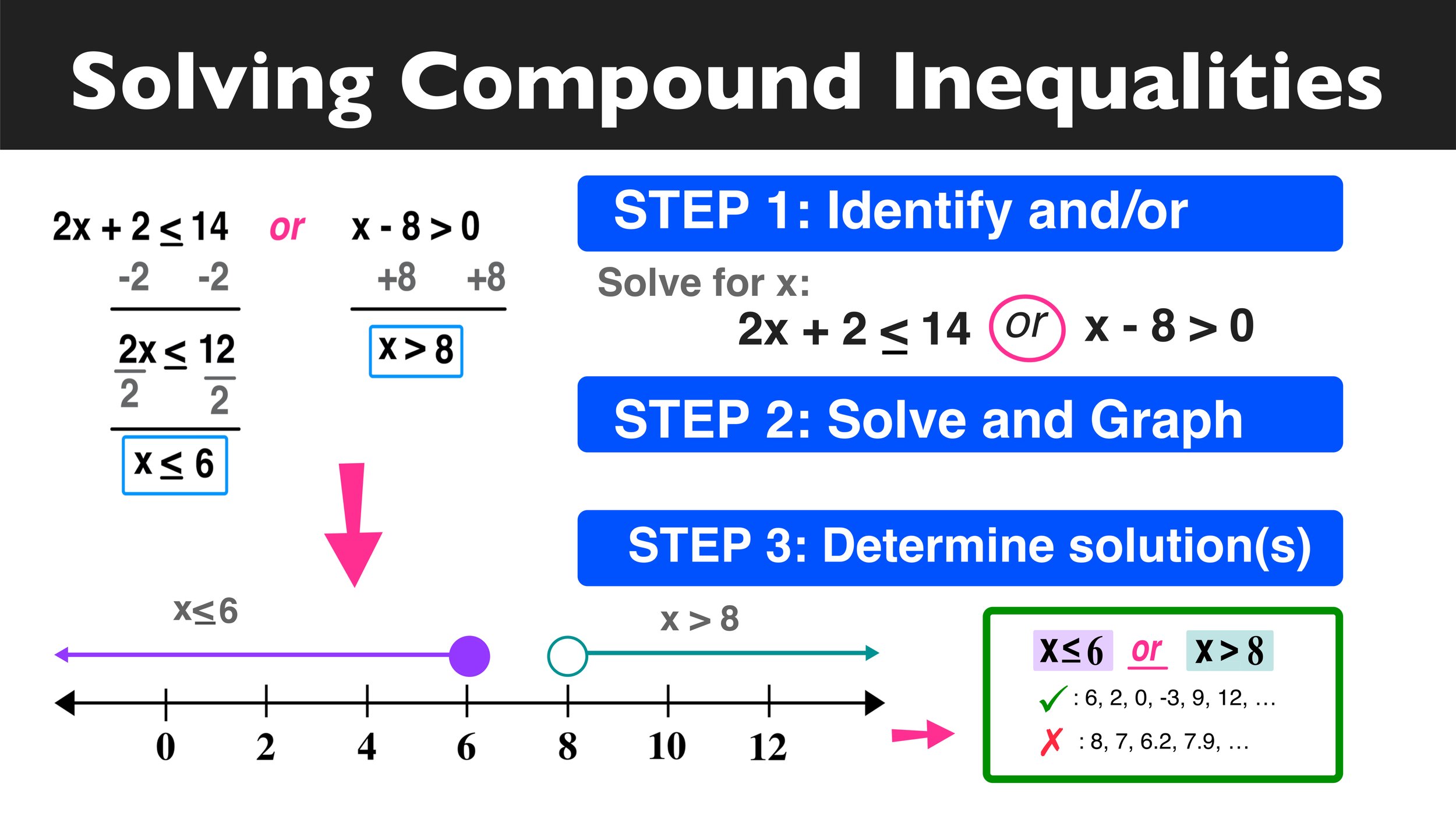
OR Inequalities

Now, consider solving an OR inequality:
-3 < x OR x < 4
This means x can be less than -3 or greater than or equal to 4. The solution involves:
- Two separate inequalities:
-∞ < x < -3 OR 4 < x < ∞
- On a number line, you would have two shaded regions: one from -∞ to -3 and another from 4 to ∞, with arrows indicating that the shading extends indefinitely.
Real-World Applications

Understanding compound inequalities isn't just about solving abstract math problems; it has practical applications:
- Designing safe limits: Engineers might use inequalities to ensure a device functions within safe temperature ranges.
- Financial Planning: Budgeting often involves setting bounds for expenditures where compound inequalities define allowable spending.
Worksheet Answers

Here are solutions to common problems on an Algebra 1 worksheet for compound inequalities:
| Question | Solution |
|---|---|
| -3 < x + 5 < 8 | -8 < x < 3 |
| x - 2 < -1 OR x + 3 > 7 | x < 1 OR x > 4 |
| 2x - 1 < 7 OR 3x + 4 < 16 | x < 4 OR x < 4 |
| 5 > x > -5 | -5 < x < 5 |

💡 Note: Remember to always verify the range of solutions on a number line after solving compound inequalities to ensure all conditions are met.
In your journey through algebra, understanding compound inequalities is fundamental. Whether you are determining feasible outcomes in a science experiment or setting realistic expectations in real-world applications, these inequalities provide the tools to navigate complex problems. By practicing with worksheets like the ones above, you'll sharpen your ability to solve these problems with ease, making algebra an enjoyable and insightful subject.
What is the difference between an AND and OR compound inequality?

+
The main difference is the solution set. With an AND compound inequality, both conditions must be satisfied simultaneously, leading to a single solution range. With an OR compound inequality, at least one of the conditions needs to be true, creating potentially disjoint solution sets.
Can compound inequalities have solutions for all real numbers?
+
Yes, in some cases. For example, if you have an OR compound inequality where one part always holds true (like x < ∞), then all real numbers would be a valid solution set.
Why do we use shading on the number line when solving inequalities?

+
Shading on a number line represents all the numbers that satisfy the inequality. Open circles indicate that the endpoint is not included, and closed circles show that the endpoint is part of the solution.